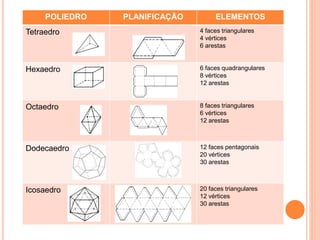
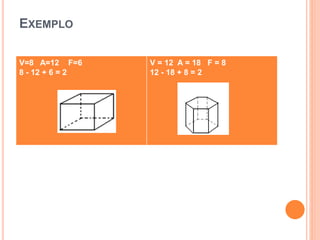
Existem cinco poliedros regulares definidos por suas faces e elementos: o tetraedro com 4 faces triangulares, o hexaedro com 6 faces quadrangulares, o octaedro com 8 faces triangulares, o dodecaedro com 12 faces pentagonais e o icosaedro com 20 faces triangulares. Estes poliedros seguem a relação de Euler que relaciona o número de vértices, arestas e faces.

1. POLIEDROS REGULARES
Um poliedro convexo é chamado de
regular se suas faces são polígonos
regulares, cada um com o mesmo
número de lados e, para todo vértice,
converge um mesmo número de arestas.
Existem cinco poliedros regulares:

2. POLIEDRO PLANIFICAÇÃO ELEMENTOS
Tetraedro 4 faces triangulares
4 vértices
6 arestas
Hexaedro 6 faces quadrangulares
8 vértices
12 arestas
Octaedro 8 faces triangulares
6 vértices
12 arestas
Dodecaedro 12 faces pentagonais
20 vértices
30 arestas
Icosaedro 20 faces triangulares
12 vértices
30 arestas

3. RELAÇÃO DE EULER
Em todo poliedro convexo é válida a
relação seguinte:
V - A + F = 2
em que V é o número de vértices, A é o
número de arestas e F, o número de
faces.

4. EXEMPLO
V=8 A=12 F=6
8 - 12 + 6 = 2
V = 12 A = 18 F = 8
12 - 18 + 8 = 2

5. POLIEDROS PLATÔNICOS
Diz-se que um poliedro é platônico se, e somente se:
a) for convexo;
b) em todo vértice concorrer o mesmo número de
arestas;
c) toda face tiver o mesmo número de arestas;
d) for válida a relação de Euler.
Assim, nas figuras anteriores, o primeiro
poliedro é platônico e o segundo, não-platônico.

6. REFERÊNCIAS BIBLIOGRÁFICAS
_______________ Geometria Espacial,
disponível em:
http://www.somatematica.com.br/emedio/espacial/e
spacial9.php. Acesso em 14/05/2012.