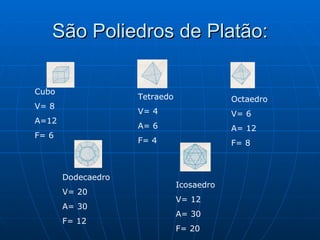
O documento discute os poliedros de Platão, que são os cinco sólidos regulares estudados por Platão. São eles: cubo, tetraedro, octaedro, dodecaedro e icosaedro. O texto também define o que é um poliedro e lista seus elementos principais como faces, vértices e arestas. Por fim, exemplifica o uso da fórmula de Euler para calcular vértices e arestas em poliedros convexos.

1. POLIEDROS DE PLATÃO

2. Poliedros ou particularmente sólidos de Platônicos, tem sido estudados há milhares de anos. Platão já destacava a beleza das formas dos cinco sólidos regulares: cubo, tetraedro, octaedro, dodecaedro e icosaedro .

3. “Poliedro é uma reunião de um número finito de polígonos planos, onde cada lado de um desses polígonos é também lado de um, e apenas um, outro polígono”, podendo ser côncavo ou convexo.

4. Os poliedros convexos possuem nomes especiais, de acordo com o número de faces: Tetraedro: poliedro convexo com quatro faces; Pentaedro: poliedro convexo com cinco faces; Hexaedro: poliedro convexo com seis faces; Heptaedro: poliedro convexo com sete faces; Octaedro: poliedro convexo com oito faces; Icosaedro: poliedro convexo com vinte faces.

5. São elementos dos poliedros: Face Vértice Aresta Um poliedro convexo é regular quando todas as faces são polígonos regulares iguais, e em todos os vértices concorrem o mesmo número de arestas.

6. São Poliedros de Platão: Cubo V= 8 A=12 F= 6 Tetraedo V= 4 A= 6 F= 4 Octaedro V= 6 A= 12 F= 8 Dodecaedro V= 20 A= 30 F= 12 Icosaedro V= 12 A= 30 F= 20

7. Relação de Euler: Em todos os poliedros convexos, podemos notar que vale a relação de Euler: V – A + F = 2

8. Exercício: Usando a relação de Euler determine o número de arestas e de vértices de um poliedro convexo com seis faces quadragulares e quatro faces triangulares:

9. Solução 6 faces quadrangulares – 6X4 = 24 arestas 4 faces triangulares – 4X3 = 12 arestas Número total de arestas = 36 Como cada aresta foi contada duas vezes, temos: 2ª = 36 A = 18 Aplicando a relação de de Euler temos: A + 2 = V + F 18 + 12 =