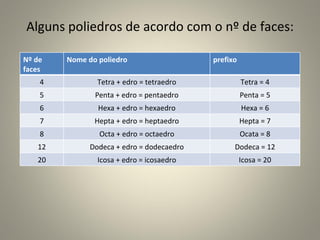
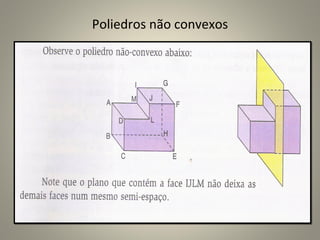
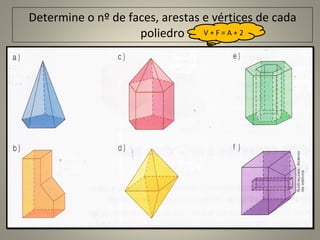
O documento descreve os principais tipos de sólidos geométricos, divididos em poliedros e corpos redondos. Poliedros são formas delimitadas por superfícies planas poligonais, sendo nomeados de acordo com o número de faces, como tetraedro (4 faces), pentaedro (5 faces) e assim por diante. Os elementos de um poliedro são vértices, arestas e faces. Alguns exemplos de poliedros convexos e não convexos são apresentados.

1. Sólidos geométricos ou poliedros Cada sólido desse grupo tem todas suas superfícies planas: Os sólidos desse grupo tem algumas superfícies não planas:

2. É possível separar os sólidos geométricos em dois grandes conjuntos: Os poliedros e os corpos redondos Def.: Os poliedros são formas espaciais sólidas delimitadas por superfícies planas poligonais. O nome poliedro vem do grego. Poli vem do grego polys e significa, muitos ou vários , e edro vem do grego hedra e significa, face . Poliedro figura de muitas faces. Num poliedro tem-se: vértices – arestas e faces. Os poliedros serão nomeados a partir do número de faces.

3. Alguns poliedros de acordo com o nº de faces: Nº de faces Nome do poliedro prefixo 4 Tetra + edro = tetraedro Tetra = 4 5 Penta + edro = pentaedro Penta = 5 6 Hexa + edro = hexaedro Hexa = 6 7 Hepta + edro = heptaedro Hepta = 7 8 Octa + edro = octaedro Ocata = 8 12 Dodeca + edro = dodecaedro Dodeca = 12 20 Icosa + edro = icosaedro Icosa = 20

4. Os elementos de um poliedro Os lados dos polígonos ► arestas do poliedro Os vértices dos polígonos ► vértices do poliedro Cada polígono que compõe o poliedro ► faces do poliedro Obs.: cada aresta é comum aos lados de dois polígonos; Os vértices são os pontos de encontro das arestas do poliedro; O menor nº de arestas que chegam a um vértice► 3

5. Alguns poliedros

6. Poliedros convexos Def.: Um poliedro é dito convexo se, em relação a qualquer de suas faces, está todo situado num mesmo semiespaço determinado pelo plano que contém esta face.

7. Poliedros não convexos

8. Num poliedro convexo é observado as seguintes situações: O número mínimo de faces de um poliedro convexo é 4 (tetraedro); Não há dois polígonos no mesmo plano; Cada lado de um polígono é comum a dois e apenas dois polígonos; O plano de cada polígono deixa todos os outros polígonos de um mesmo ‘lado’ desse plano.

9. Exercícios básicos Classifique em poliedro ou não poliedro (corpo redondo) as figuras sólidas abaixo:

10. Determine o nº de faces, arestas e vértices de cada poliedro V + F = A + 2

11. Classifique cada poliedro em convexo e não convexo:

12. Determine quais polígonos correspondem as faces dos poliedros: