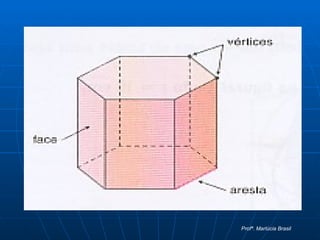
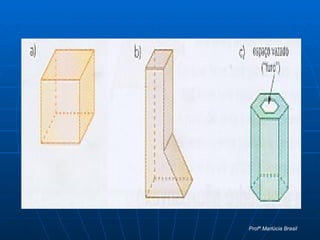
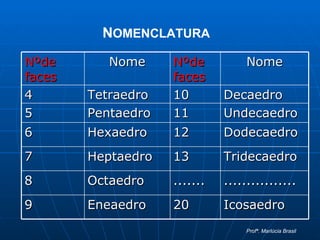
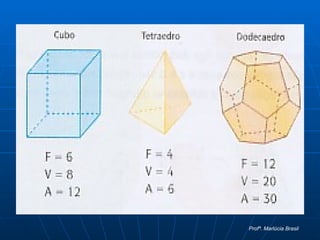
O documento define poliedros como sólidos limitados por polígonos planos, onde dois polígonos não estão no mesmo plano e cada lado é compartilhado por dois polígonos. Poliedros podem ser convexos, com todas as faces em um mesmo semi-espaço, ou não convexos. A relação de Euler relaciona o número de vértices, arestas e faces de um poliedro convexo.

1. P rofª. Marlúcia Brasil Colégio Manoel Novaes

2. DEFINIÇÃO Denomina-se poliedro o sólido limitado por polígonos planos,de modo que: . Dois desse polígonos não estão num mesmo plano; . Cada lado de um polígono é comum a dois e somente dois polígonos; Profª. Marlúcia Brasil

3. ELEMENTOS DE UM POLIEDRO Os polígonos são denominados faces do poliedro. Os lados e os vértices dos polígo-nos denominam-se respectiva-mente, arestas e vértices do poliedro. Profª.Marlúcia Brasil

4. Profª. Marlúcia Brasil

5. RECORDANDO: A região de um polígono com os pontos interiores a ele é chamada de região poligonal .Essa região é convexa se, e somente se,a reta r que contém qualquer um dos lados do polígono deixa todos os pontos da região poligonal em um mesmo semiplano de origem r. Profª.Marlúcia Brasil

6. Profª.Marlúcia Brasil

7. POLIEDRO CONVEXO E POLIEDRO NÃO- CONVEXO Um poliedro se diz convexo , em relação a qualquer de suas faces,está todo situado num mesmo semi-espaço determinado pelo plano que contém esta face.Caso contrá-rio, o poliedro é dito não-convexo . Profª.: Marlúcia Brasil

8. Profª.Marlúcia Brasil

9. N OMENCLATURA Profª. Marlúcia Brasil Nºde faces Nome Nºde faces Nome 4 Tetraedro 10 Decaedro 5 Pentaedro 11 Undecaedro 6 Hexaedro 12 Dodecaedro 7 Heptaedro 13 Tridecaedro 8 Octaedro ....... ................ 9 Eneaedro 20 Icosaedro

10. POLIEDROS REGULARES Um poliedro convexo é regular se,e somente se, são satisfeitas as seguintes condições: I)Todas as suas faces são regiões poligonais regulares e congruen-tes entre si; II)Todos os seus ângulos poliédri-cos são congruentes entre si. Profª.:Marlúcia Brasil

11. Profª.:Marlúcia Brasil

12. A RELAÇÃO DE EULER O matemático suíço Leonhard Euler (1707-1783) descobriu uma importante relação entre o nº de vértices,nº de arestas e o nº de faces de um poliedro convexo. Profª.:Marlúcia Brasil

13. Profª. Marlúcia Brasil

14. Dentre suas contribuições à geometria espacial, Euler demonstrou o teorema: Em todo poliedro convexo cujo número de vértices é V , o número de arestas é A e o número de faces é F , vale a relação: V – A + F = 2 Profª. Marlúcia Brasil

15. Aplicação da Relação de Euler (pág.384),LIVRO MANOEL PAIVA. 1 .Um icosaedro convexo possui todas as faces triangulares. Quantas arestas possui esse poliedro? 2 .Um poliedro convexo é constituído por três faces triangulares,cinco qua- drangulares e sete pentagonais.Quan- tas arestas possui esse poliedro? Profª. Marlúcia Brasil

16. Atividade proposta : Livro de Matemática Autor Manoel Paiva Página 384,exercício 09 ao 16 Profª.:Marlúcia Brasil Colégio Manoel Novaes