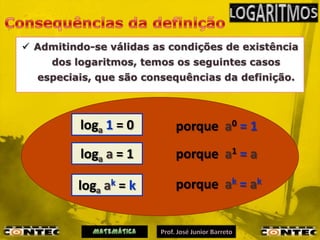
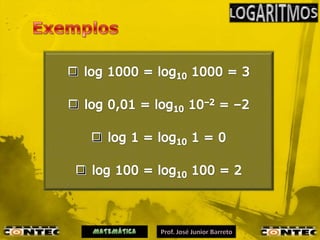
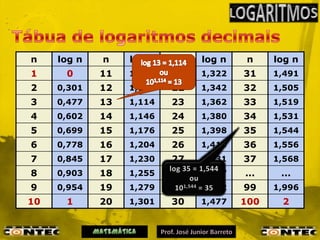
Neste documento, são apresentados os seguintes tópicos sobre logaritmos: 1) A definição básica de logaritmo relaciona o expoente de uma potência com o logaritmo de sua base; 2) São mostradas propriedades fundamentais como a aditividade de logaritmos de produtos e a subtratividade de logaritmos de quocientes; 3) É explicado o cálculo de logaritmos utilizando tábuas ou propriedades algébricas.

5. Capital aplicado: C = 1 000
Taxa: 5 % ao mês = 0,05 ao mês
Montante pretendido: M = 1 500,00
M = C.(1 + i)t ⇒ 1 500 = 1 000 . (1,05)t
⇒ 1,05t = 1,5 1,057 ≈ 1,407
1,058 ≈ 1,477
1,059 ≈ 1,551

7.  A invenção dos logaritmos ocorreu no
início do século XVII e é creditada ao
escocês John Napier e ao suíço
Jobst Burgi.
 Inicialmente seu objetivo era
SIMPLIFICAR OS CÁLCULOS NUMÉRICOS,
principalmente em problemas ligados à
Astronomia e à Navegação.

10. 1 = 100 0,1 = 10–1
10 = 101 0,01 = 10–2
100 = 102 0,001 = 10–3
1 000 = 103 0,0001 = 10–4
10 000 = 104 0,00001 = 10–5

11. 2 = 100,301
11 = 101,041
3 = 100,477
13 = 101,114
7 = 100,845

12.  4 = 22 = (100,301)2 = 10 0,602
10 = 10 = 101 – 0,301
 5 = 2 100,301 = 10 0,699
 6 = 2.3 = 10 0,301
. 100,477 = 100,301 + 0,477
= 100,778

13.  60 = 2.3.10 = 10 0,301 . 10 0,477 . 10
⇒ 60 = 10 0,301 + 0,477 + 1
⇒ 60 = 10 1,778

14. 2x = 12 ⇒ 2x = 22.3
⇒ (100,301)x = (100,301)2 . 100,477
⇒ 100,301.x = 100,602 . 100,477
⇒ 100,301.x = 101,079
1,079
⇒ 0,301.x = 1,079 ⇒ x = ⇒ x ≈ 3,585
0,301

15. log2 8 = 3

16. Vale, portanto a equivalência:
log2 8 = 3 ⇔ 23 = 8
Calcular um logaritmo é obter um expoente.
Logaritmo é o mesmo que expoente.

17. loga b = x ⇔ ax = b
 a é a base  x é o logaritmo
 b é o logaritmando ou antilogaritmo

18.  log2 32 = 5, porque 25 = 32
 log3 (1/81) = –4, porque 3–4 = 1/81
 log10 0,001 = –3, porque 10–3 = 0,001
3 3
 log5 √25 = 2/3, porque 52/3 = √25
De acordo com a definição, calcular um
logaritmo é descobrir o expoente, ou seja,
resolver uma equação exponencial.

19. Calcular log4 8.
log4 8 = x ⇒ 4x = 8
⇒ (22)x = 23
⇒ 22x = 23
⇒ x = 3/2

20. 5
Calcular log1/3 √9.
x
5 5
log1/3 √9 = x ⇒ 1 = √9
3
⇒ (3–1)x = 32/5 ⇒ –x = 2/5
⇒ 3–x = 32/5 ⇒ x = –2/5

21. b>0
loga b = x ⇔ a>0
a≠ 1

22. Analise quais seriam os significados
de log2 (–4), log(–2) 8, log7 0, log1 6 e
log0 2, caso fossem definidos.
log2 (–4) = x ⇒ 2x = –4 impossível
log–2 8 = x ⇒ (–2)x = 8 impossível
log7 0 = x ⇒ 7x = 0 impossível
log1 6 = x ⇒ 1x = 6 impossível
log0 2 = x ⇒ 0x = 2 impossível

23.  Admitindo-se válidas as condições de existência
dos logaritmos, temos os seguintes casos
especiais, que são consequências da definição.
loga 1 = 0 porque a0 = 1
loga a = 1 porque a1 = a
loga ak = k porque ak = ak

24. log3 3 = log10 10 = log3,7 3,7 = 1
log3 1 = log10 1 = log3,7 1 = 0
log3 39 = 9
log10 10–3 = –3

26. log x → logaritmo decimal de x (base 10)

28.  O primeiro a utilizar os logaritmos
decimais foi o matemático inglês
Henry Briggs (1561-1631).
 Foi ele quem construiu a primeira
tábua de logaritmos decimais.

29. n log n n log n n log n n log n
1 0 11 1,041 21 1,322 31 1,491
2 0,301 12 1,079 22 1,342 32 1,505
3 0,477 13 1,114 23 1,362 33 1,519
4 0,602 14 1,146 24 1,380 34 1,531
5 0,699 15 1,176 25 1,398 35 1,544
6 0,778 16 1,204 26 1,415 36 1,556
7 0,845 17 1,230 27 1,431 37 1,568
8 0,903 18 1,255 28 1,447 ... ...
9 0,954 19 1,279 29 1,462 99 1,996
10 1 20 1,301 30 1,477 100 2

32.  Vamos calcular o valor do log 21, a partir dos
valores de log 3 = 0,477 e log 7 = 0,845.
log 3 = 0,477 ⇒ 100,477 = 3
log 7 = 0,845 ⇒ 100,845 = 7
⇒ 10x = 21
log 21 = xlog (3.7) = log 3 + log 7
log 21 =
⇒ 10x = 3.7 ⇒ 10x = 100,477.100,845
⇒ 10x = 100,477 + 0,845
⇒ x = 0,477 + 0,845 ⇒ x = 1,322

33.  De modo geral, o logaritmo do
produto de dois números, numa certa
base, é a soma dos logaritmos desses
números, na mesma base.
Loga (x.y) = loga x + loga y
OBS: Para o produto de três ou mais fatores, a
propriedade continua válida.

34. A partir de log 2 = 0,301 e log 13 =
1,114, calcular log 26 e log 2000.
 log 26 = log (2.13) = log 2 + log 13
log 26 = 0,301 + 1,114 = 1,415
 log 2000 = log (2.1000) = log 2 + log 1000
log 2000 = 0,301 + 3 = 3,301

35. Transformar num único logaritmo e
calcular o valor da expressão
log 4 + log 5 + log 50.
log 4 + log 5 + log 50 = log (4.5.50)
log 4 + log 5 + log 50 = log 1000= 3

36.  Vamos calcular o valor do log (3/2), a partir dos
valores de log 2 = 0,301 e log 3 = 0,477.
log 2 = 0,301 ⇒ 100,301 = 2
log 3 = 0,477 ⇒ 100,477 = 3
log (3/2) = x ⇒ 10x = 3/2= log 3 – log 2
log (3/2)
3 100,477
⇒ 10x = = = 100,477 – 0,301
2 100,301
⇒ x = 0,477 – 0,301 ⇒ x = 0,176

37.  De modo geral, o logaritmo do
quociente de dois números, numa
certa base, é a diferença dos
logaritmos desses números, na
mesma base.
Loga (x/y) = loga x – loga y

38. A partir de log 2 = 0,301 obter log 5.
10
log 5 = log = log 10 – log 2
2
⇒ 1 – 0,301
⇒ log 5 = 0,699

39.  Vamos calcular o valor do log 34, a
partir do valor de log 3 = 0,477.
log 3 = 0,477 ⇒ 100,477 = 3
log 34 = x ⇒ 10x = 34 ⇒ 10x = (100,477)4
⇒ x = 4 . 0,477 ⇒ x = 1,908
log 34 = 4 . log 3

40.  Generalizando, o logaritmo de uma
potência, é igual ao produto do expoente
da potência pelo logaritmo da base.
Loga xk = k . loga x

41. A partir do log 3 = 0,477, calcular log 0,009.
9
log 0,009 = log = log 9 – log 100
100
= log 32 – 2 = 2 . log 3 – 2
= 2 . 0,477 – 2
= 0,954 – 2 = – 1,046

44.  Na tábua de logaritmos decimais, encontramos
que log10 23 = 1,362 e log10 7 = 0,845. A partir
deles, determine o valor log7 23.
log10 23 = 1,362 ⇒ 101,362 = 23
log10 7 = 0,845 ⇒ 100,845 =10 23
log 7
log7 23 =
log7 23 = x ⇒ 7 x = 23 log10 7
⇒ (100,845)x = 101,362 ⇒ 100,845.x = 101,362
1,362
⇒ 0,845.x = 1,362 ⇒ x = = 1,612
0,845

45.  De modo geral, podemos calcular
logba, utilizando uma outra base k
arbitrária. Para isso, dividimos o
logaritmo de a pelo logaritmo de b, na
base k escolhida.
logk a
Logb a =
logk b

46. Resolver a equação 5x = 20, dados os
logaritmos decimais
log 5 = 0,699 e log 20 = 1,301.
5x = 20 ⇒ x = log5 20
log10 20 log 20 1,301
log5 20 = = = = 1,861
log10 5 log 5 0,699