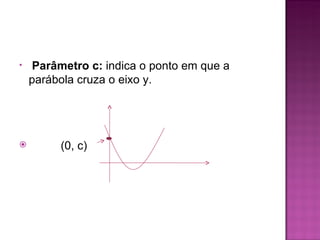
O documento discute o conceito de função quadrática e parábola, incluindo suas propriedades e elementos como vértice, raízes e gráfico. Explica que uma função quadrática é dada por f(x) = ax2 + bx + c e que seu gráfico forma uma parábola, cuja concavidade depende do sinal de a e cujo vértice tem coordenadas xv = -b/2a e yv = -Δ/4a.

1. Prof: Fábio F Dias

2.  Denomina-se equação do segundo grau,
toda a equação do tipo ax²+bx+c, com
coeficientes numéricos a.b e c com a
diferente de zero.

3.  3x²-7x+2=0
 x² - 4x =0
 x² - 4 =0

5. = (-7)²-4.3.2 = 49-24 = 25

7. AS ORIGENS DA PARÁBOLA
Não há unanimidade sobre como a curva plana conhecida como parábola
foi introduzida na matemática. Segundo a versão mais difundida, ela teria
surgido dos esforços de Menaecmo (c. IV a.C.), um discípulo de
Aristóteles (384-322 a.C.), para resolver o chamado “problema deliano”,
cuja origem é muito curiosa.
Assolados por uma devastadora peste, os habitantes da ilha de Delos
(os delianos) recorreram aos préstimos de seu oráculo, que sugeriu ,
para afastar o mal, que eles construíssem um altar cúbico cujo volume
fosse o dobro do já existente consagrado ao deus Apolo. E a parábola tem
sua
origem na busca dessa solução.

13. Chama-se função quadrática ou função polinomial
do 2 º
grau, qualquer função f de R em R dada por uma lei
da
forma f(x) = ax2 +bx + c, em que a, b e c são
números
reais e a ≠ 0.

14. Veja alguns exemplos de funções quadráticas:
 f(x) = 2 x2 + 3x + 5, sendo a = 2, b = 3 e c =
5
 f(x) = 3 x2 - 4x + 1, sendo a = 3, b = - 4 e c
=1
 f(x) = x2 - 1, sendo a = 1, b = 0 e c = - 1
 f(x) = - x2 + 2x, sendo a = - 1, b = 2 e c = 0
 f(x) = - 4 x2 , sendo a = - 4, b = 0 e c = 0

15. O grafico da função Polinomial do 2° grau
f(x) = ax2 + bx + c, com a ≠ 0, é uma curva
chamada parabola.

16. y
f(x) = x2 - 3x + 2 4
3
x f(x)
2
-1 6
1
0 2
1 0
x
−4 −3 −2 −1 1 2 3 4 5
2 0 −1
3 2
−2
−3
−4

17.  Significado dos parâmetros a, b e c no gráfico da função quadrática
• Parâmetro a: responsável pela concavidade e abertura da parábola.
 Se a > 0 a concavidade é para cima. Se a < 0 a concavidade é para
baixo.
Parâmetro b: indica se a parábola cruza o eixo y com seu ramo crescente ou
decrescente. Se b > 0 a parábola cruza o eixo y no ramo crescente. Se b <
0 a parábola cruza o eixo y no ramo decrescente.

18. • Parâmetro c: indica o ponto em que a
parábola cruza o eixo y.
 (0, c)

19. ZEROS OU RAÍZES DA FUNÇÃO QUADRÁTICA
Zeros ou raízes da função quadrática f(x)= ax2 + bx + c são os valores de x para os
quais a função se anula, ou seja, f(x) = 0. Assim, os zeros da função quadrática f(x)=
ax2 +bx +c são as soluções da equação do 2º grau ax2 +bx + c = 0, as quais são
dadas pela fórmula:
x = - b ± √ b2 – 4ac
2a
Vamos obter os zeros da função f(x) = x2 - 3x + 2.
Temos a = 1, b = - 3 e c = 2
Então, aplicando a fórmula, as raízes são: x’ = 1 e x’’ = 2.

20. Duas raízes reais e diferentes
Duas raízes reais e iguais
Nenhuma raiz real

21. VÉRTICE DA PARÁBOLA
O vértice da parábola, gráfico da função f(x)= ax2 + bx + c, tem
coordenadas xv = - b (abscissa) e yv = - ∆ (ordenada). Assim, o vértice
2a 4a
da parábola é o ponto V - b , - ∆ .
2a 4a
Se a > 0, o vértice é ponto de mínimo da função.
Se a < 0, o vértice é ponto de máximo da função.
V(xv , yv)
ponto de máximo
V(xv , yv)
ponto de mínimo

22. Um time de praia montou um campo de futebol de 100 m de
comprimento por 70 m de largura e, por medida de segurança, decidiu
cercá-lo, deixando entre o campo e a cerca uma pista com 3 m de
largura. Qual é a área do terreno limitado pela cerca?
3
100
campo 3
3 70
pista 3

23. A área da região cercada é:
(100 + 2 . 3) (70 + 2 . 3) = 106 . 76 = 8 056 m2
Se a largura da pista fosse de 4 m, a área da região cercada seria:
(100 + 2 . 4) (70 + 2 . 4) = 108 . 78 =8 424 m2
Observe que a cada largura x da pista, há uma área A(x) da região
cercada. E que o valor de A(x) é uma função de x dada pela expressão:
A(x) = (100 + 2x) (70 + 2x) =
= 7 000 + 200x + 140x + 4 x2
= 4 x2 + 340x + 7 000
Esse é um caso particular de função quadrática ou função polinomial
do 2 º grau.

24. BIBLIOGRAFIA:
DANTE, L. R. (2005) Matemática. São Paulo: Editora Ática.
IEZZI, G.et al. (2004) Matemática: Ciência e Aplicações. 2ª Ed. São Paulo:
Atual