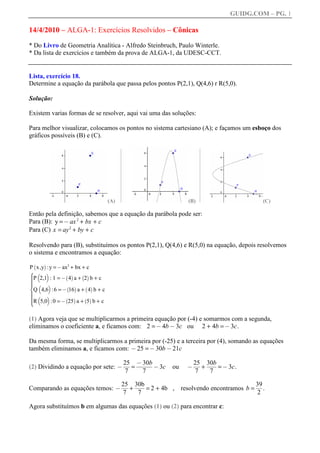
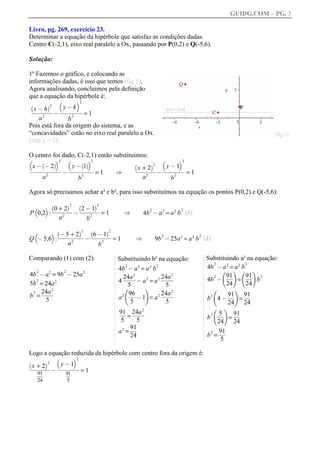
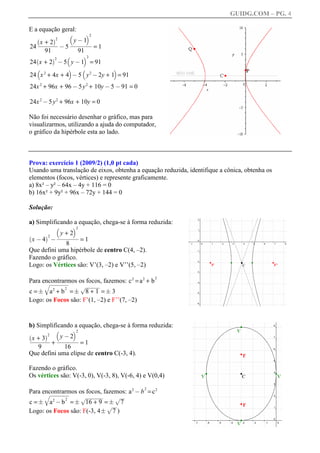
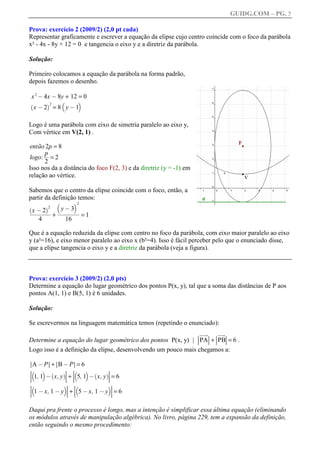
1) O documento apresenta a resolução de dois exercícios sobre cônicas, incluindo a determinação da equação de uma parábola e hipérbole. 2) É também apresentada a resolução de exercícios sobre cônicas tirados de provas, incluindo obter a forma reduzida de equações e identificar elementos geométricos. 3) Por fim, é resolvido um exercício sobre determinar a equação do lugar geométrico de pontos cuja soma das distâncias a dois pontos fixos é constante.

1. GUIDG.COM – PG. 1
14/4/2010 – ALGA-1: Exercícios Resolvidos – Cônicas
* Do Livro de Geometria Analítica - Alfredo Steinbruch, Paulo Winterle.
* Da lista de exercícios e também da prova de ALGA-1, da UDESC-CCT.
Lista, exercício 18.
Determine a equação da parábola que passa pelos pontos P(2,1), Q(4,6) r R(5,0).
Solução:
Existem varias formas de se resolver, aqui vai uma das soluções:
Para melhor visualizar, colocamos os pontos no sistema cartesiano (A); e façamos um esboço dos
gráficos possíveis (B) e (C).
(A) (B) (C)
Então pela definição, sabemos que a equação da parábola pode ser:
Para (B): y = @ ax 2 + bx + c
Para (C) x = ay 2 + by + c
Resolvendo para (B), substituímos os pontos P(2,1), Q(4,6) e R(5,0) na equação, depois resolvemos
o sistema e encontramos a equação:
P x ,y :y = @ax2 + bx + c
` a
X b c
^P 2,1 : 1 = @ ` 4a a + `2a b + c
^
^
^
^
^
^ b c
^
Q 4,6 : 6 = @ 16 a + 4 b + c
` a ` a
^
^ b c
^
^
^
ZR 5,0 :0 = @ 25 a + 5 b + c
^
^ ` a ` a
^
(1) Agora veja que se multiplicarmos a primeira equação por (-4) e somarmos com a segunda,
eliminamos o coeficiente a, e ficamos com: 2 = @ 4b @ 3c ou 2 + 4b = @ 3c .
Da mesma forma, se multiplicarmos a primeira por (-25) e a terceira por (4), somando as equações
também eliminamos a, e ficamos com: @ 25 = @ 30b @ 21c
25f @ffff
ff fffff
ff f30bf
f
f ffff
= ffff@ 3c @ ff+ fff= @ 3c .
25f 30bf
ff fff
f
f ff
ff
(2) Dividindo a equação por sete: @ ou
7 7 7 7
25f 30bf
ff fff
ff fff
f
f
+ ff = 2 + 4b , resolvendo encontramos b = ff
ff 39f
ff
f
f
Comparando as equações temos: @ .
7 7 2
Agora substituímos b em algumas das equações (1) ou (2) para encontrar c:

2. GUIDG.COM – PG. 2
f g
39f
ff
ff
f
f @fff
ffff
f80f
fff
fff
2+4 = @ 3c , resolvendo encontramos c = .
2 3
Por último substituímos b e c, na primeira equação para encontrar a:
f g
17f
ff
ff
f
f
1 = @ 4 a + 2 b + c [ 1 = @ 4 a + 2 ff @ ff , resolvendo encontramos a = .
` a ` a ` a ` a 39f 80f
ff
f
f ff
ff
2 3 6
Substituindo na equação geral: y = @ ax 2 + bx + c = @ ffx 2 + ffx @ ff
17f
ff
ff 39f 80f
ff
f
f ff
f
f
6 2 3
Para obter a equação da parábola (C), basta seguir o mesmo procedimento, mas alterando a variável e
os coeficientes já que o gráfico esta paralelo ao eixo x: x = ffy 2 @ fffy + 5
17f
ff
f
f 107f
fff
ff
ff
30 30

3. GUIDG.COM – PG. 3
Livro, pg. 269, exercício 23.
Determinar a equação da hipérbole que satisfaz as condições dadas.
Centro C(-2,1), eixo real paralelo a Ox, passando por P(0,2) e Q(-5,6).
Solução:
1º Fazemos o gráfico, e colocando as
informações dadas, é isso que temos (fig.1).
Agora analisando, concluímos pela definição
que a equação da hipérbole é:
b c2
` a2 yffffff
kfff
@ffff
xffffff ffff
@h
fffffff fff fff
ffffff
ffffff fff
f
@ =1
a2 b
2
Pois está fora da origem do sistema, e as
“concavidades” estão no eixo real paralelo a Ox. (fig.1)
(reta y = 1)
O centro foi dado, C(-2,1) então substituímos:
b ` ac2 b ` ac2 b c2
+ffff fffffff
x ffffffff fffffff
@ @2 y@ 1 ` a2 y ff1ff
@f
ffffffffff ffffffff
ffffffffff ffffffff
fffffffff
f xffffff fffffff
2ff ffffff
2
@ fffffff= 1
2
[ ffffff
ffff
ff f
@ =1
a b a2 b
2
Agora só precisamos achar a² e b², para isso substituímos na equação os pontos P(0,2) e Q(-5,6):
c `0 + 2a2 `2 @ 1a2
ffffff ffffff
ffffff ffffff
ffffff ffffff
ffffff ffffff
b
=1 4b @ a 2 = a 2 b (1)
2 2
P 0,2 : @ [
a2 b
2
c `@ 5 + 2a2 `6 @ 1a2
ffffffff ffffff
ffffffff ffffff
ffffffff ffffff
fffffff ffffff
b
=1 9b @ 25a 2 = a 2 b (2)
2 2
Q @ 5,6 : @ [
a2 b
2
Comparando (1) com (2): Substituindo b² na equação: Substituindo a² na equação:
4b @ a 2 = a 2 b
2 2
4b @ a 2 = a 2 b
2 2
4b @ a = 9b @ 25a
2 2 2 2 f g f g
4b @ ff = ff b
2 2 91f 91f 2
ff
f
f ff
f
f
4 ffff a 2 = a 2 ffff
24aff
fff
fff
ff 24aff
fff
fff
ff 2
5b = 24a 2
2 @ 24 24
5 5
2
b = ffff
24aff
fff
fff
ff
f g 2
a 2 ff 1 = a 2 ffff
2 96f
ff
f
f 24aff
fff
fff
ff
f g
4 @ ff = ff
@ 2 91f 91f
ff ff
ff f
f
5 5 5 b
24 24
2
91f 24aff
ff ffff
ff fff
ff fff
= ff
f g
5f 91f
ff
ff ff
ff ff
f
f
=
2
5 5 b
24 24
a 2 = ff
91f
ff
f
f
b = ff
2 91f
ff
f
f
24
5
Logo a equação reduzida da hipérbole com centro fora da origem é:
b c2
+ffff fffffff
` a2 y ff1 ff
@f
xffffff fffffff
ffffff
ffff
ff 2ff ffffff
f
91f
@ 91 =1
ff
ff
ff
f
f ff
ff
ff
f
24 5

4. GUIDG.COM – PG. 4
E a equação geral:
b c2
+2
` a2 y ff1 ff
@
xffffff
ffffff
ffffff
ffffff
24 @ 5 fffffff 1
fffffff
ffffff
f f
=
91 91
b c2
24 x + 2 @ 5 y @ 1 = 91
` a2
b c b c
24 x 2 + 4x + 4 @ 5 y 2 @ 2y + 1 = 91
24x 2 + 96x + 96 @ 5 y 2 + 10y @ 5 @ 91 = 0
24x 2 @ 5 y 2 + 96x + 10y = 0
Não foi necessário desenhar o gráfico, mas para
visualizarmos, utilizando a ajuda do computador,
o gráfico da hipérbole esta ao lado.
Prova: exercício 1 (2009/2) (1,0 pt cada)
Usando uma translação de eixos, obtenha a equação reduzida, identifique a cônica, obtenha os
elementos (focos, vértices) e represente graficamente.
a) 8x² – y² – 64x – 4y + 116 = 0
b) 16x² + 9y² + 96x – 72y + 144 = 0
Solução:
a) Simplificando a equação, chega-se à forma reduzida:
b c2
+2
y fffff
x @ 4 @ fffffff 1
fffffff
ffffff
f
=
` a2
8
Que defini uma hipérbole de centro C(4, –2).
Fazendo o gráfico.
Logo: os Vértices são: V’(3, –2) e V’’(5, –2)
Para encontrarmos os focos, fazemos: c 2 = a 2 + b
2
wwww
wwww
wwww
wwww
wwww
wwww
www
www
www
www
www
www
www
www
www
ww
c = F qa 2 + b = F p8 + 1 = F 3
2
Logo: os Focos são: F’(1, –2) e F’’(7, –2)
b) Simplificando a equação, chega-se à forma reduzida:
b c2
+f
` a2 yffffff
2ff
@ffff
xffffff ffff
fff3ff fff
ffffff ffffff
ffffff f
+ =1
9 16
Que defini uma elipse de centro C(-3, 4).
Fazendo o gráfico.
Os vértices são: V(-3, 0), V(-3, 8), V(-6, 4) e V(0,4)
Para encontrarmos os focos, fazemos: a 2 @ b = c 2
2
wwww
wwww
wwww
wwww
wwww
wwww
wwww
www
wwww
wwww
wwww
www
www
www
www
www w
w
w
w
ww
w
c = F qa 2 @ b = F p16 + 9 = F p 7
2
w
ww
w
w
ww
Logo: os Focos são: F(-3, 4 F p 7 )

5. GUIDG.COM – PG. 5
Prova: exercício 2 (2009/2) (2,0 pt cada)
Representar graficamente e escrever a equação da elipse cujo centro coincide com o foco da parábola
x² - 4x - 8y + 12 = 0 e tangencia o eixo y e a diretriz da parábola.
Solução:
Primeiro colocamos a equação da parábola na forma padrão,
depois fazemos o desenho.
x 2 @ 4x @ 8y + 12 = 0
b c
x @2 =8 y@1
` a2
Logo é uma parábola com eixo de simetria paralelo ao eixo y,
Com vértice em V(2, 1) .
então 2p = 8
logo: ff 2
pf
ff
=
2
Isso nos da a distância do foco F(2, 3) e da diretriz (y = -1) em
relação ao vértice.
Sabemos que o centro da elipse coincide com o foco, então, a
partir da definição temos:
b c2
` a2 yffffff
3ff
@ffff
xffffff ffff
@2
fffffff ffffff
ffffff
ffffff fff
f
+ =1
4 16
Que é a equação reduzida da elipse com centro no foco da parábola, com eixo maior paralelo ao eixo
y (a²=16), e eixo menor paralelo ao eixo x (b²=4). Isso é fácil perceber pelo que o enunciado disse,
que a elipse tangencia o eixo y e a diretriz da parábola (veja a figura).
Prova: exercício 3 (2009/2) (2,0 pts)
Determine a equação do lugar geométrico dos pontos P(x, y), tal que a soma das distâncias de P aos
pontos A(1, 1) e B(5, 1) é 6 unidades.
Solução:
Se escrevermos na linguagem matemática temos (repetindo o enunciado):
Ljk Ljj
jj jj
jj j M
jj j
jM
j
j
j
j jj
k
j
j
Determine a equação do lugar geométrico dos pontos P(x, y) | LPAM+LPBM= 6 .
L M L M
Logo isso é a definição da elipse, desenvolvendo um pouco mais chegamos a:
LA @ PM+LB @ PM= 6
L M L M
Lb c ` M L M
M b c `
L 1, 1 @ x, y M+L 5, 1 @ x, y M= 6
L a L aM
L M L M
Lb c L
M b cM
L 1 @ x, 1 @ y M+L 5 @ x, 1 @ y M= 6
L M L M
L M L M
Daqui pra frente o processo é longo, mas a intenção é simplificar essa última equação (eliminando
os módulos através de manipulação algébrica). No livro, página 229, tem a expansão da definição,
então seguindo o mesmo procedimento:

6. GUIDG.COM – PG. 6
5x2 @ 30x + 9 y 2 @ 18y + 9 = 0
Ou fatorando (completando os quadrados e tal...) chegamos à equação reduzida:
b c2
` a2 yffffff
1ff
@ffff
xffffff ffff
@3
fffffff fff fff
ffffff
ffffff fff
f
+ =1
9 5
Ou seja, uma elipse com eixo maior paralelo ao eixo dos x, e eixo menor paralelo ao eixo dos y, com
centro em C(3, 1).
E por curiosidade (o exercício não pede), o gráfico: