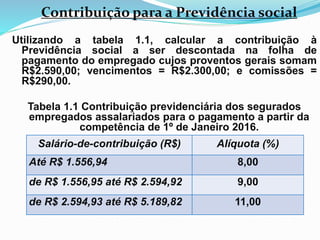
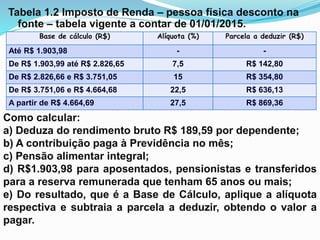
O documento explica o conceito de porcentagem e como calcular valores após aumentos ou descontos percentuais. É apresentado que porcentagem é uma razão especial e como transformar porcentagens em frações decimais. Exemplos demonstram cálculos de preços com acréscimos e reduções percentuais usando fatores de aumento e redução.

1. PORCENTAGEM

2. PORCENTAGEM
As situações envolvendo porcentagem
estão cada vez mais presentes no nosso
dia-a-dia. Podemos encontrá-las lendo um
jornal ou revista, consultando gráficos ou
tabelas, ou até mesmo fazendo algum tipo
de compra.

3. PORCENTAGEM
Frequentemente, ouvimos expressões como:
“O rendimento da poupança em Março foi de 0,65%”.
“Desconto de 8% na semana do Natal”.
“O índice de reajuste salarial da categoria é de 3,48%”.
“A inflação de dezembro foi de 0,87%”.
“Os preços foram majorados em 1,22%”.
Essas expressões envolvem uma razão especial denominada
porcentagem ou percentagem.

4. TRANSFORMANDO PORCENTAGENS
EM FRAÇÕES
25
14
100
56
%56
10
3
100
30
%30
10
1
100
10
%10




5. PORCENTAGEM
Para compreendermos o que é uma porcentagem temos que
saber claramente o que é uma razão, as razões com
denominador 100 (razões centesimais) podem ser expressas
em forma de porcentagem:

6. EXEMPLOS
 De um grupo de 100 jogadores, 30 praticam
basquete. Isso significa que 30% (trinta por cento)
dos jovens praticam basquete.
 Num lote de 50 lâmpadas, 13 apresentam defeito; a
razão entre o número de lâmpadas defeituosas e o
total de lâmpadas é dada por:

7. PORCENTAGEM
 Outra maneira de representar porcentagem é por
meio de um número decimal.
 4% =

►37% = 0,37 ►80% = 0,80 = 0,8
►14,5% = 0,145 ►100% = 1
►250% = 2,50 = 2,5 ►0,7% = 0,007
04,0
100
4


8. EXEMPLO
 Uma torta é vendida por R$ 32,00. Se seu preço
aumentar em 20%, quanto passaria a custar?
Temos:
(1º) o aumento seria 20% de 32 = 0,2 x 32 = 6,40
(2º) o novo preço seria 32 + 6,40 = R$ 38,40.
Poderíamos fazer simplesmente:
Observe que o preço inicial fica multiplicado por 1,2.
40,382,132 

9. Portanto, se tivéssemos:
♦ Um aumento de 30% multiplicaria o preço por 1,3;
♦ Um aumento de 16% multiplicaria o preço por 1,16;
♦ Um aumento de 5% multiplicaria o preço por 1,05;
Se por outro lado a torta fosse anunciada com um
desconto de 20% sobre o preço original, a torta
passaria a custar:
Observe que o preço fica multiplicado por 0,8.
60,258,032 

10. Assim, se tivéssemos:
♦ Desconto de 30% multiplicaríamos o preço original
por 0,7;
♦ Desconto de 16% multiplicaríamos o preço original
por 0,84;
♦ Desconto de 5% multiplicaríamos o preço original
por 0,95

11. Contribuição para a Previdência social
Utilizando a tabela 1.1, calcular a contribuição à
Previdência social a ser descontada na folha de
pagamento do empregado cujos proventos gerais somam
R$2.590,00; vencimentos = R$2.300,00; e comissões =
R$290,00.
Tabela 1.1 Contribuição previdenciária dos segurados
empregados assalariados para o pagamento a partir da
competência de 1º de Janeiro 2016.
Salário-de-contribuição (R$) Alíquota (%)
Até R$ 1.556,94 8,00
de R$ 1.556,95 até R$ 2.594,92 9,00
de R$ 2.594,93 até R$ 5.189,82 11,00

12. Tabela 1.2 Imposto de Renda – pessoa física desconto na
fonte – tabela vigente a contar de 01/01/2015.
Base de cálculo (R$) Alíquota (%) Parcela a deduzir (R$)
Até R$ 1.903,98 - -
De R$ 1.903,99 até R$ 2.826,65 7,5 R$ 142,80
De R$ 2.826,66 e R$ 3.751,05 15 R$ 354,80
De R$ 3.751,06 e R$ 4.664,68 22,5 R$ 636,13
A partir de R$ 4.664,69 27,5 R$ 869,36
Como calcular:
a) Deduza do rendimento bruto R$ 189,59 por dependente;
b) A contribuição paga à Previdência no mês;
c) Pensão alimentar integral;
d) R$1.903,98 para aposentados, pensionistas e transferidos
para a reserva remunerada que tenham 65 anos ou mais;
e) Do resultado, que é a Base de Cálculo, aplique a alíquota
respectiva e subtraia a parcela a deduzir, obtendo o valor a
pagar.

13. Calcule o salário líquido de funcionário que ganha
R$5.245,66 de salário bruto, sabendo-se que ele tem
três dependentes.

14. FATORES DE AUMENTO E DE
REDUÇÃO
Para facilitar o cálculo de reajustes e de descontos percentuais,
vamos trabalhar com fatores de aumento e de redução. É
importante lembrar que o termo fatores está relacionado à
operação de multiplicação. Essa será, portanto, a principal
ferramenta que você vai utilizar para fazer os cálculos com
porcentagem.

15. EXEMPLOS
Uma mercadoria que custa R$ 80,00 deve sofrer um desconto
de 40%. A porcentagem a pagar por essa mercadoria será,
então, de 100% – 40%, que é igual a 60%. Veja seu valor já
com o desconto:
0,60 x R$ 80,00 = R$ 48,00
Uma mercadoria que custa R$ 80,00 deve sofrer um aumento
de 40%. A porcentagem a pagar por essa mercadoria, depois
do aumento, será de 100% + 40%, que é igual a 140%. Veja:
1,40 x R$ 80,00 = R$ 112,00

16. No caso em que conhecemos os valores antes e depois do
desconto ou aumento, podemos encontrar os percentuais
correspondentes. Veja;
Numa liquidação, o preço de uma mercadoria passou de
R$20,00 para R$18,00. Qual foi a taxa percentual de
desconto?
Para encontrarmos o preço com desconto, usamos a operação
de multiplicação; agora, usaremos sua inversa, que é a
divisão. Basta dividir o preço com desconto pelo preço
inicial:
Como vimos anteriormente, 0,90 é o mesmo que 90%. O preço
pago corresponde, então, a 90% do preço inicial, que era de
100%. Portanto o desconto foi de 100% – 90% = 10%.
90,0
00,20$R
00,18$R


17. Uma loja vendia um determinado produto por R$80,00.
Decidiu reajustá-lo para R$96,00. Qual foi a porcentagem
de aumento?
Vamos dividir o valor final pelo valor antes do aumento:
Sabemos que 1.20 é igual a 120%, e que o valor percentual
antes do aumento era de 100%. O aumento percentual
corresponde, então, a
120% – 100% = 20%.
Podemos concluir que, para encontrarmos o percentual de
aumento ou de redução em um valor, basta dividir o valor final
pelo valor inicial.
Vi = valor inicial
Vf = valor final
20,1
00,80$R
00,96$R


18. No caso, (1 + i) é o fator que deve ser multiplicado pelo valor
inicial para se obter o valor final, aumentado segundo uma taxa
percentual i. Por isso, ele é chamado fator de aumento (ou de
reajuste). Vf = Vi (1 + i)
Analogamente, (1 – i) é o fator que deve ser multiplicado pelo
valor inicial para se encontrar o valor final, reduzido segundo
um percentual i. Ele é chamado, por isso, fator de redução (ou
de desconto). Vf = Vi (1 – i)






ipercentual)desconto(reduçãoi1
ipercentual)reajuste(aumentoi1
V
V
i
f

19. Calculando um valor após
aumentos e descontos sucessivos
Uma indústria produziu, em janeiro deste ano, 1 500 unidades de um
certo produto. De janeiro para fevereiro, sua produção aumento 12%
e, de fevereiro para Março, sofreu uma redução de 10%. Quantas
unidades foram produzidas em Março?
Percentual de aumento de janeiro para fevereiro: i = 12% = 0,12
Fator de aumento de janeiro para fevereiro: 1 + i = 1 + 0,12 = 1,12
Percentual de redução de fevereiro para março: i = 10% = 0,10
Fator de redução de fevereiro para março: 1 – i = 1 – 0,10 = 0,90
A produção de março é obtida, multiplicando-se 1 500,
produção de janeiro, pelo fator de aumento de fevereiro e pelo fator
de redução de março:
Vf = Vi (1 + i)(1 – i)
1 500 . 1,12 . 0,90 = 1 512

20. Uma mercadoria sofre um reajuste de 10%: em seguida, novo
reajuste de 20%; finalmente, um desconto de 30%. Terá a
mercadoria voltado ao valor inicial? Se não, qual terá sido o
percentual final de reajuste ou de desconto?
Quando um valor sofre reduções ou aumentos consecutivos, o
caminho não é somar ou subtrair percentuais, mas multiplicar
fatores de aumento e de redução.
(1 + i)(1 + i)(1 – i) = 1,10 . 1,20 . 0,70 = 0,924
Como obtivemos um produto menor que 1, isso significa que, no final de
tudo, houve um desconto. De quanto? É só descobrir quanto falta em 0,924
para chegar a 1. Basta subtrair 1 – 0,924 = 0,076 = 7,6%. Portanto, em
relação ao preço inicial, houve um desconto de 7,6%.