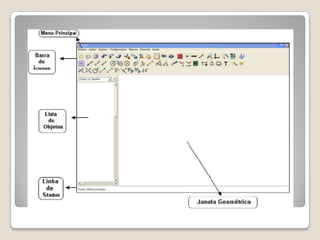
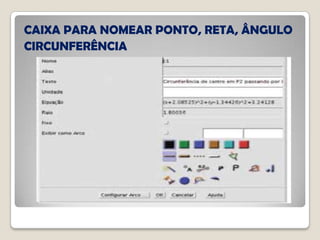
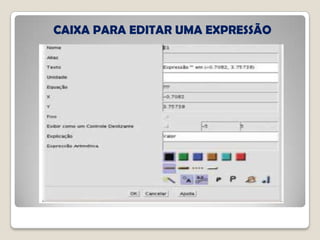
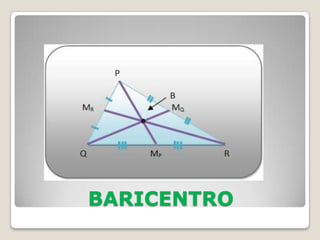
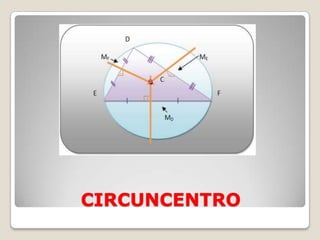
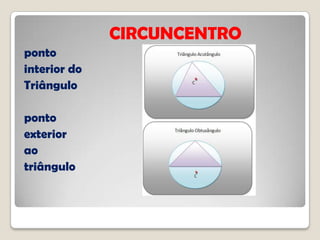
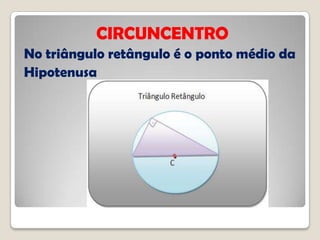
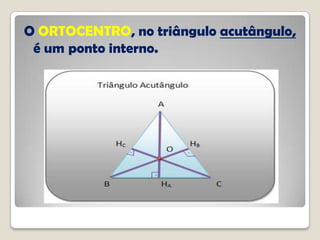
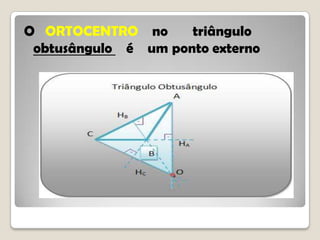
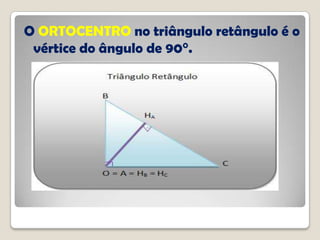
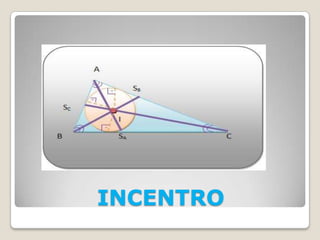
O documento discute conceitos geométricos de triângulos, incluindo pontos notáveis como o baricentro, circuncentro e ortocentro. É apresentado um software de geometria dinâmica para explorar essas propriedades através de construções. Os alunos são instruídos a realizar várias tarefas usando o software para compreender melhor esses pontos e características dos triângulos.

1. 8º Ano Ensino Fundamental
Professora Carmen Beatriz Pacheco
OS NOTÁVEIS DE UM
TRIÂNGULO

2. JUSTIFICATICA
O estudo da Geometria constitui parte
importante no currículo, visto que os alunos
desenvolvem a capacidade de compreender,
descrever e representar de forma organizada o
espaço em que vivem.
Este projeto fará uso do Software Régua e Compasso
onde poderemos explorar a geometria com maior
agilidade e melhor visualização, proporcionando
aos alunos, conteúdos do currículo de maneira que
a construção do conhecimento seja de forma
prazerosa e efetiva.

3. Vamos agora construir dois triângulos com
as mesmas dimensões usando a cartolina.
Agora pense e responda:
Existe um ponto D pertencente ao triângulo
que seja possível suspendê-lo através de
um barbante, deixando-o em equilíbrio?

4. Procurem este ponto, de modo a
suspender o triângulo,
equilibrando-o através do
barbante
Existe alguma técnica para resolver
este problema?

5. Vamos assistir ao vídeo
” A COMUNIDADE”

6.  Você gostou do vídeo?
 O que você viu?
 O que você sentiu?
 O que ouviu?
 O que você aprendeu?
 Utilize agora o outro triângulo que você
construiu e tente encontrar o seu ponto de
equilíbrio, lembrando das informações do vídeo.
Leitura de imagem relativa às informações contidas no vídeo: O que você viu? O que você sentiu? O que ouviu? O que você aprendeu?Leitura de imagem relativa às informações contidas no vídeo: O que você viu? O que você sentiu? O que ouviu? O que você aprendeu?Leitura de imagem relativa às informações contidas no vídeo: O que você viu? O que você sentiu? O que ouviu? O que você aprendeu?Leitura de imagem relativa às informações contidas no vídeo: O que você viu? O que você sentiu? O que ouviu? O que você aprendeu?

7. Pesquise na internet e/ ou livros sobre os os
pontos notáveis de um triângulo e
exemplos práticos.
Após a pesquisa, com o seu grupo, faça
uma breve explanação do seu trabalho.

8. Conhecendo o software Régua e Compasso
É um programa de geometria dinâmica, isto é
sua função é possibilitar o trabalho com
construções geométricas que podem ser
alteradas movendo um dos pontos básicos,
permitindo a preservação das propriedades
originais. Dessa forma permite explorar diversos
aspectos relativos à Geometria Plana
Euclidiana e à Geometria Analítica.
www.professores.uff.br

10. BARRA DE FERRAMENTAS

11. CAIXA PARA NOMEAR PONTO, RETA, ÂNGULO
CIRCUNFERÊNCIA

12. CAIXA PARA EDITAR UMA EXPRESSÃO

13. CONSTRUÇÃO DO BARICENTRO DE UM
TRIÂNGULO
Processo de construção:
1- Determinar três pontos A, B e C.
2- Na função segmento traçar segmento de reta
dos pontos AB, BC e CA.
3- Na função ponto médio determinar o ponto
médio de cada um desses segmentos.
4- Na função ponto marcar os pontos D, E e F,
pontos médios dos lados.
5- Na função segmento traçar a mediana de
cada lado do triângulo.

14. 6- Na função ponto marcar G ponto de
intersecção das medianas.
7- G é o Baricentro do triângulo.
8- Com a ferramenta mover ponto, mover os
vértices A, B e C.
* O que acontece com a figura?
* E se movimentarmos os pontos médios do lado
do triângulo: D, E e F, o que acontece? Fazer
todos os registros.
* Explique com suas palavras o que é o baricentro
de um triângulo.

15. Mediana
 A mediana de um triângulo é o segmento
compreendido entre o vértice e o ponto
médio do lado oposto a esse vértice.
 As três medianas de uma triângulo
encontram-se em um ponto interior
chamado de BARICENTRO.

16. BARICENTRO

17.  O baricentro também pode ser
chamado de centro de gravidade do
triângulo, dividindo assim cada
mediana dentro da razão de 2:1.

18. Construção do circuncentro de um triângulo
Processo de construção:
1- Desenhar um triângulo ABC.
2-Marcar os pontos médios D, E e F dos lados AB,
BC e AC.
3- Na função perpendicular, traçar a
perpendicular de cada lado do triângulo
passando pelo seu médio. Cada reta traçada
representa a mediatriz de um lado do triângulo.
4- Pelas construções feitas o que você entende por
mediatriz?

19. 5- Marcar o ponto de intersecção das três
perpendiculares e nomeá-la por T Esse ponto
recebe o nome de circuncentro.
6- Registrar o que você entendeu sobre o
significado de circuncentro.
7- Com a ferramenta mover os pontos mover os
vértices A, B ou C do triângulo, o ponto G,
circuncentro do triângulo passa a ocupar
diferentes localizações:
a) Quando o circuncentro estará na região
interna da figura?

20. b) Quando o circuncentro estará sobre um dos
lados da figura?
c) Quando o circuncentro estará na região
externa da figura?
8-Por que o circuncentro é equidistante dos
vértices do triângulo ABC?

21. Mediatriz
A mediatriz de cada lado do triângulo
é uma reta perpendicular, passando
pelo ponto médio do lado do
triângulo.
As três mediatrizes de um triângulo
encontram-se em um ponto chamado
CIRCUNCENTRO.

22. CIRCUNCENTRO

23. CIRCUNCENTRO
ponto
interior do
Triângulo
ponto
exterior
ao
triângulo

24. CIRCUNCENTRO
No triângulo retângulo é o ponto médio da
Hipotenusa

25. Construção do ortocentro de um
triângulo
Processo de construção:
1- Desenhar um triângulo ABC.
2- Na função perpendicular, traçar a
perpendicular de cada lado do triângulo
passando pelo vértice oposto a cada lado.
3- Marcar o ponto de intersecção de cada lado e
nomeá-lo por “ O “.
4- O ponto “ O ” é o ortocentro do triângulo ABC.
5- Escreva o que você entendeu sobre o que vem a
ser o ortocentro por meio das construções.

26. 6- Movimentar o vértice A e observar as medidas
dos ângulos internos da figura e registrar o que
acontece quando:
a) o ortocentro está na parte interna do
triângulo?
b) o ortocentro está na parte externa do
triângulo?
c) o ortocentro coincide com um dos três vértices
do triângulo?
7- Mover o vértice B, ou o vértice C do triângulo e
verificar se ocorrem as mesmas observações
anteriores.

27. Altura
A altura de um triângulo é um segmento
perpendicular a um lado de um triângulo
e de origem no vértice oposto a esse lado.
As três alturas de um triângulo encontram-
se em um único ponto chamado de
ORTOCENTRO.
O ORTOCENTRO pode ser externo ao
triângulo.

28. O ORTOCENTRO, no triângulo acutângulo,
é um ponto interno.

29. O ORTOCENTRO no triângulo
obtusângulo é um ponto externo

30. O ORTOCENTRO no triângulo retângulo é o
vértice do ângulo de 90°.

31. Construção do Incentro de um
triângulo
Processo de construção:
1- Desenhar um triângulo ABC.
2- Na função bissetriz traçar a bissetriz de
cada ângulo desse triângulo.
3- Marcar a intersecção das bissetrizes.
Nomeá-la com a letra I.
4- O que você entendeu por bissetriz?

32. 5- “ I “ é um elemento de destaque no
triângulo. Por quê? Que nome ele recebe?
6- Por que o ponto “ I “ equidista dos lados
do triângulo?
7- De acordo com a sua construção,
observação e análise, o que vem a ser
incentro?

33. Bissetriz
As três bissetrizes internas do triângulo
encontram-se em um único ponto
interior chamado de INCENTRO.
O INCENTRO é o único ponto
equidistante dos três lados.
O INCENTRO é o centro de uma
circunferência inscrita no triângulo.

34. INCENTRO

35. Em um triângulo isósceles a Mediana,
Bissetriz, Mediatriz e a Altura relativa a
base ( lado diferente), coincidem-se.
No triângulo equilátero, a Bissetriz, a
Mediana e a Altura são coincidentes.
Portanto, em um triângulo equilátero, o
ORTOCENTRO, INCENTRO, BARICENTRO e
CIRCUNCENTRO são coincidentes

36. Desafios
Utilizando o Software régua e compasso e utilizando os
conceitos de Pontos Notáveis de um triângulo, resolver
em dupla os seguintes problemas:
1-Sua família tem um terreno em forma triangular. Eles
querem instalar uma luminária em cada lateral do
terreno de modo a gastar a menor quantidade possível
de fio para instalar três luminárias, uma em cada
parede (aresta), do terreno a partir de um ponto
interior do terreno equidistante das três laterais do
triângulo.
● Como determinar um ponto equidistante de todas as
paredes (arestas) de um triângulo?

37. 2- Onde uma empresa de telefonia deve instalar
uma antena para celulares em um bairro de
uma cidade, considerando três pontos quaisquer
deste bairro, de tal forma que o sinal do celular
atinja, estes três pontos, com a mesma
intensidade do sinal do celular.
3- Dados os pontos A, B e C, determine a
circunferência que os contenha esses pontos.

38. “Aquele que tentou e não
conseguiu é superior
aquele que nada tentou.”
Arquimedes