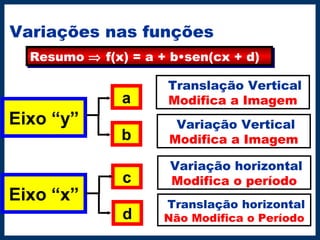
O documento descreve as funções seno e cosseno, suas propriedades e variações possíveis através de fatores multiplicativos, translações e alterações no argumento. É mostrado como esses fatores modificam a imagem e o período da função. Como exemplo, é analisada a função f(x)=1+sen(2x).

2. Função Seno
f(x) =
sen(x)
π/2
0π
3π/2
x sen
-13π/2
π/2 1
0 0
π 0
2π 0
y
x0 π/2 π
3π/2 2π
1
-1
Período = 2π
Imagem = [-1, 1]
2π
Função Ímpar

3. Função Cosseno
f(x) =
Cos(x)π/2
0π
3π/2
x cos
03π/2
π/2 0
0 1
π -1
2π 1
y
x0 π/2 π
3π/2 2π
1
-1
Período = 2π
Imagem = [-1, 1]
2π
Função Par

4. Variações nas funções
1º Caso ⇒ f(x) = a • sen(x)1º Caso ⇒ f(x) = a • sen(x)
1
-1
a
-a
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = a • sen(x)
Imagem = [- a, a]
Período = 2π
2π

5. Variações nas funções
K•f(x) Estica K vezes
1/k•f(x) Encolhe k vezes
Variação Vertical
Modifica a Imagem

6. Variações nas funções
Exemplo ⇒ f(x) = 2sen(x)
1
-1
2
-2
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = 2sen(x)
Imagem = [- 2, 2]
Período = 2π
2π

7. Variações nas funções
2º Caso ⇒ f(x) = b + sen(x)2º Caso ⇒ f(x) = b + sen(x)
1
-1
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = b + sen(x)
Imagem = [-1+b, 1+b]
Período = 2π
1+b
-1+b
2π

8. Variações nas funções
f(x) + k SOBE k UNIDADES
f(x) - k DESCE K UNIDADES
Translação Vertical
Modifica a Imagem

9. Variações nas funções
Exemplo ⇒ f(x) = 1 + sen(x)
1
-1
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = 1 + sen(x)
Imagem = [0, 2]
Período = 2π
0
2
2π

11. Variações nas funções
3º Caso ⇒ f(x) = sen(c•x)3º Caso ⇒ f(x) = sen(c•x)
1
-1
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = sen(c•x)
Imagem = [-1, 1]
Período = 2π/|c|
2π2π/IcI

12. Variações nas funções
f(k•x) DIMINUI K VEZES
O PERÍODO
f(1/k•x) AUMENTA K VEZES
O PERÍODO
Variação Horizontal
Modifica o Período
Variação Horizontal
Modifica o Período

13. Variações nas funções
1
-1
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = sen(2x)
Imagem = [-1, 1]
Período = 2π/2= π
2ππ
Exemplo ⇒ f(x) = sen(2x)Exemplo ⇒ f(x) = sen(2x)

14. Variações nas funções
4º Caso ⇒ f(x) = sen(x + d)4º Caso ⇒ f(x) = sen(x + d)
1
-1
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = sen(x + d)
Imagem = [-1, 1]
Período = 2π
2π

15. Variações nas funções
f(x-k) MOVE PARA DIREITA
K UNIDADES
f(x+k) MOVE PARA ESQUERDA
K UNIDADES
Translação Horizontal
Não Modifica o Período

16. Variações nas funções
1
-1
f(x) = sen(x)
Imagem = [-1, 1]
Período = 2π
f(x) = sen(x + d)
Imagem = [-1, 1]
Período = 2π
π
Exemplo ⇒ f(x) = sen(x + π)
π

17. Variações nas funções
Resumo ⇒ f(x) = a + b•sen(cx + d)Resumo ⇒ f(x) = a + b•sen(cx + d)
Translação Vertical
Modifica a Imagem
Variação Vertical
Modifica a Imagem
Eixo “y”
Eixo “x”
a
b
d
c
Variação horizontal
Modifica o período
Translação horizontal
Não Modifica o Período

18. Variações nas funções
Exemplo ⇒ f(x) = 1 + sen(2x)
1
-1
2
Período = 2π/2= π
2ππ
Imagem = [0, 2]
1º) y = sen(2x)
2º) y = 1 + sen(2x)

19. Sugestão de exercícios:
CAPÍTULO 07
Questões: 261, 263, 264, 269, 277, 279, 287, 292 e 299.