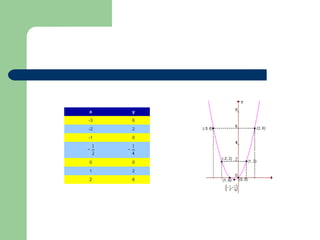
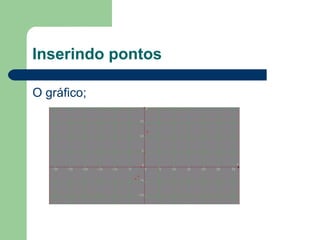
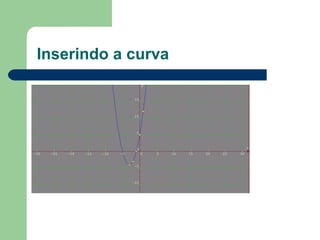
O documento descreve um curso sobre funções quadráticas, abordando conceitos como gráficos, vértice e zeros. Aprendizagem é feita através de aulas expositivas, resolução de exercícios e atividades no laboratório com software. O curso tem o objetivo de ensinar conceitos e aplicações de funções quadráticas.

1. FUNÇÃO QUADRÁTICA
Curso de Informática
Educativa
Aluna: Carla C. A. de
Oliveira
Pólo: Duque de Caxias

2. Conceitos trabalhados:
 Situações onde aparecem a função
quadrática;
 Valor numérico;
 Zero da função;
 Forma canônica;
 Gráfico da função;
 Vértice;

3. 1ª aula:
Pré-requisitos
 Introdução com uma apresentação histórica;
 Para que serve?
 Como se apresenta?
2ª aula:
 Fórmula de Bháskara;
 Vértice;

4. 3ª aula
Exemplos
 Quais das seguintes funções são
quadráticas?
 A) y= 2x²
 B) y= 2/x²
 C) y= 2x + 1
 D) y= x² + x

5. Onde podemos utilizar?
 Nos fenômenos físicos:
Qual o espaço percorrido por um corpo
após 2 segundos de queda livre? Sabendo
que a forma aplicada é S(t)=4,9t²
Onde s é o espaço percorrido e m função do
tempo(t).

6. 4ª aula-No esporte:
 Calculando
a distância e a altura da bola em
um lançamento livre com direção ao gol.

7. Na geometria:
 Calculandoo número de diagonais de um
polígono convexo.

8. 5ª aula-A turma será dividida em
grupos de 6 alunos, para:
 Encontrarpossíveis soluções para o
problema gerador:
“ Os diretores de um centro esportivo desejam cercar uma
quadra de basquete retangular e o espaço em volta dela com
tela de alambrado. Tendo recebido 200 metros de tela os
diretores desejam saber quais devem ser as dimensões?”
De que forma calcular? Debate.

9. 6ª aula: Estudar as possíveis soluções
 Após 30 minutos, os alunos, com uma
postura investigativa, poderão apresentar
para turma suas soluções.
 Solução:(100-x).x = 100x – x²
 Ou f(x)= -x² + 100x
 Sendo assim uma função quadrática.

10. Atividades
 1 - Determine a função f(x) = ax + b, sabendo-se que f(2) = 5 e f(3) = -10.
SOLUÇÃO:
Podemos escrever:
5 = 2.a + b
-10 = 3.a + b
Subtraindo membro a membro, vem:
5 - (- 10) = 2.a + b - (3.a + b)
15 = - a a = - 15
Substituindo o valor de a na primeira equação (poderia ser na segunda), fica:
5 = 2.(- 15) + b b = 35.
Logo, a função procurada é: y = - 15x + 35.

11. 2- (UCSal) - Sabe-se que -2 e 3 são raízes de uma função quadrática. Se o
–
ponto
(-1 , 8) pertence ao gráfico dessa função, então:
a) o seu valor máximo é 1,25
b) o seu valor mínimo é 1,25
c) o seu valor máximo é 0,25
d) o seu valor mínimo é 12,5
*e) o seu valor máximo é 12,5.

12.  SOLUÇÃO:
Sabemos que a função quadrática, pode ser escrita na forma fatorada:
y = a(x - x1)(x - x2) , onde x1 e x2, são os zeros ou raízes da função.
Portanto, poderemos escrever:
y = a[x - (- 2 )](x - 3) = a(x + 2)(x - 3)
y = a(x + 2)(x - 3)
Como o ponto (-1,8) pertence ao gráfico da função, vem:
8 = a(-1 + 2)(-1 - 3)
8 = a(1)(-4) = - 4.a
Daí vem: a = - 2
A função é, então: y = -2(x + 2)(x - 3) , ou y = (-2x -4)(x - 3)
y = -2x2 + 6x - 4x + 12
y = -2x2 + 2x + 12
Temos então: a = -2 , b = 2 e c = 12.
Como a é negativo, concluímos que a função possui um valor máximo.
Isto já elimina as alternativas B e D.

13.  3) Em cada um dos itens abaixo, ache o vértice, o
eixo de simetria do gráfico e a imagem de cada uma
das funções. Classifique o vértice como um ponto de
máximo ou de mínimo da função dada.
 (a) x² + 6x +5
 (b) x² - 10x + 16
 (c) 2x² - 5x + 3
 (d) x² - 8x + 12

14. 4)- Escreva a forma canônica da função
x² - 4x - 6:
Solução: x² -4x – 6 = ( x² - 4x ) – 6
= (x² - 4x + 4) -4 -6
= (x – 2)² - 10

15. 7ª aula: mais atividades
5)- determine , se existirem, os zeros da
função f(x)= 2x² - 3x + 5
Solução: a=2 b= -3 c= 5
= b² - 4ac = (-3)² - 4(2)(5) = 9 – 40= -31
= -31 < 0 = Não existem raízes

16. 8ª aula: Utilização do livro didático
 Em sala de aula: Será proposto a construção
de dois gráficos
Vamos construir o gráfico da função y = x² + x:
Primeiro atribuímos a x alguns valores,
depois calculamos o valor correspondente
de y e, em seguida, ligamos os pontos assim
obtidos.

17. x y
-3 6
-2 2
-1 0
0 0
1 2
2 6

18. Uso do laboratório: 9ª e 10ª aula
No laboratório construiremos o gráfico da
função X² + 6X + 5 com auxílio do software
graphmática.
Serão os alunos encaminhados à sala de
informática, separados por grupos

19. Inserindo pontos
O gráfico;

20. Inserindo a curva

21. Referências bibliográficas
http://www.somatematica.com.br/emedio/funcao2/funcao2.php
http://pessoal.sercomtel.com.br/matematica/fundam/eq2g/quadratica
.
htmhttp://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html
?aula=1390
http://www.im.ufrj.br/dmm/projeto/projetoc/precalculo/sala/conte
udo/capitulos/cap103.html

22. LIVROS;
*Matemática aula por aula- Xavier e Barreto -
FTD
*Matemática e ciência aplicada- Gelson Iezzi e
Osvaldo Dolce - Saraiva
*Matemática- Dante - Editora Ática