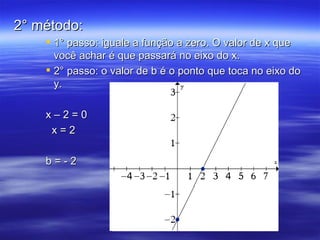
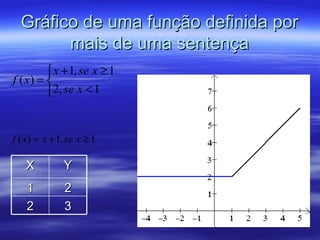
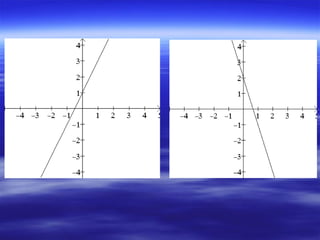
O documento discute funções do primeiro grau, definindo-as como funções polinomiais da forma f(x) = ax + b, com a ≠ 0. Explica como calcular o gráfico, determinar se uma função é crescente ou decrescente, e resolve exercícios envolvendo sistemas de equações para encontrar os valores de a e b.

1. Funções

2. Iremos estudar:
 Função do 1° grau

3. Cronograma por assunto
 Definição
 Gráficos
 Zero da Função
 Variação do sinal
 Inequação

4. Funções Polinomiais do
1º Grau
(Função Afim)

5. Pré-requisitos
 Equações do primeiro grau
 Inequações do primeiro grau
 Intervalos
 Sistemas

6. Definição
Toda função polinomial da forma
f(x) = ax + b,
com a ≠ 0 , é dita função do 1° grau.
Ex.: f(x) = 3x – 2; a = 3 e b = - 2
f(x) = - x + ½; a = -1 e b = ½
f(x) = -2x; a = -2 e b = 0

7. Casos Especiais
 Função linear b = 0, p.e., f(x) = 3x
 Função Identidade b = 0 e a = 1, ou
seja, f(x) = x
 Função constante a = 0, p.e., f(x) = 3

8. Exercícios
1°) Dada a função f(x) = ax + 2, determine o valor
de a para que se tenha f(4)=20.
f (4) = a.4 + 2, como f (4) = 20, então
4a + 2 = 20
4a = 18
18
a=
4
9
a=
2

9. 2°) Dada a função f(x) = ax + b, com a
diferente de zero, sendo f(3) = 5 e f(-2) = -
5, calcule f(1/2).
 f(3)=5: a.3 + b =5
 f(-2) = - 5: a.(-2) + b = -5
3a + b = 5

−2a + b = −5

10. Existem dois métodos para resolver esse sistema:
ADIÇÃO E SUBSTITUIÇÃO
1° ADIÇÃO: Multiplicar a primeira equação por
(-1) e somar as equações
− a −b =−
3 5 −2a +b = −5

− a +b =−
2 5 −2.2 +b = −5
− a =−
5 10 b = −5 + 4
a =2 b = −1

11. 2° SUBSTITUIÇÃO: Escolhe uma equação
isolando uma letra e depois substitui essa
letra isolada na equação que sobrou
3a + b = 5

−2a + b = −5
3a + b = 5 − 2a + b = −5
b = 5 − 3a − 2a + (5 − 3a) = −5
− 5a = −5 − 5
b = 5 − 3.2 a=2
b = −1

12. Logo, a função é f(x)= 2x – 1.
Assim,
f(1/2)=2.(1/2) - 1 = 1 – 1
f(1/2) = 0

13. Há uma outra forma de resolver esse tipo
de exercício que se conhece os valores de
uma função em dois pontos distintos.
Basta usar a fórmula:
y2 − y1
a= , x1 ≠ x2
x2 − x1
y1 x2 − y2 x1
b= , x1 ≠ x2
x2 − x1

14. Voltando a questão, quem seria esses
valores?
Temos que f(3) = 5 e f(-2) = - 5
Então, x1 = 3, y1 = 5
x2 = −2, y2 = −5
Logo,
−5 − 5 −10
a= = =2
−2 − 3 −5
5.(−2) − (−5).3 −10 + 15 5
b= = = = −1
−2 − 3 −5 −5

15. Gráficos
Toda gráfico de uma função do 1° grau é
uma reta.
Estudaremos como essa reta vai se
comportar através de cada função.

16. Como fazer um gráfico
1° método:
Para achar o gráfico de qualquer função,
basta achar dois pontos qualquer dela e
passar uma reta entre essas retas.

17. Exemplo:
f(x) = x – 2
X Y
1 -1
3 1

18. 2° método:
 1° passo: iguale a função a zero. O valor de x que
você achar é que passará no eixo do x.
 2° passo: o valor de b é o ponto que toca no eixo do
y.
x–2=0
x=2
b=-2

19. Gráfico de uma função definida por
mais de uma sentença
 x + 1, se x ≥ 1
f ( x) = 
2, se x < 1
f ( x) = x + 1, se x ≥ 1
X Y
1 2
2 3

20. Crescimento de decrescimento de
uma função
Uma função será crescente quando a>0
Uma função será decrescente quando a<0
Exemplo:
f(x) = 2x+1 a=2 crescente
f(x) = -3x+2 a = -3 decrescente

22. Qual o valor de a para que
f(x) =(2.a - 3)x+2 seja crescente?
E decrescente?
2.a – 3>0
a>3/2
2.a – 3<0
a<3/2