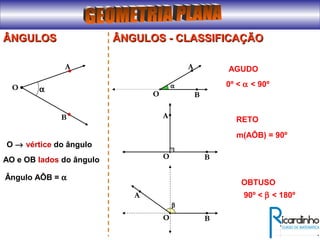
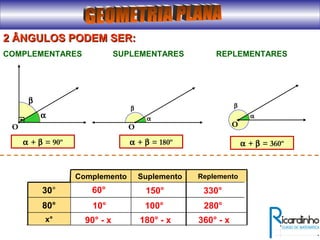
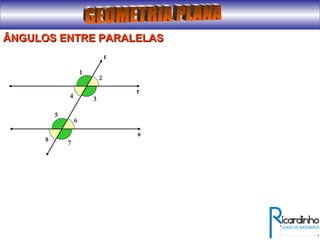
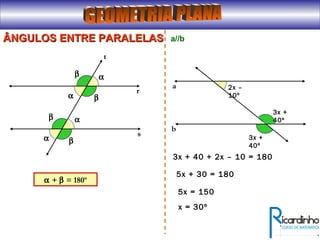
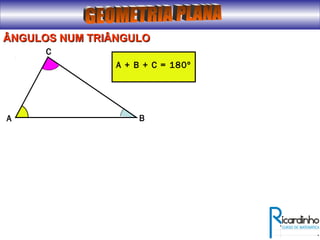
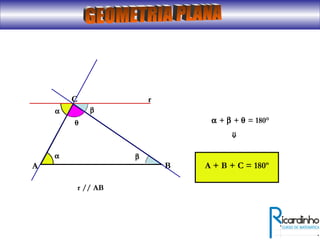
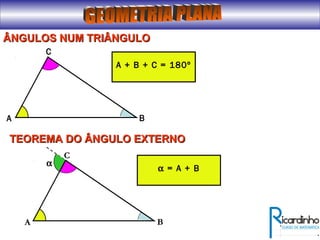
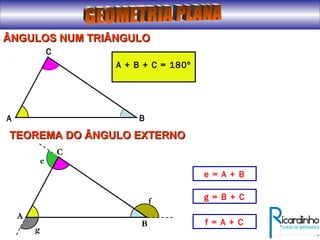
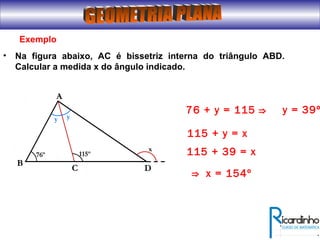
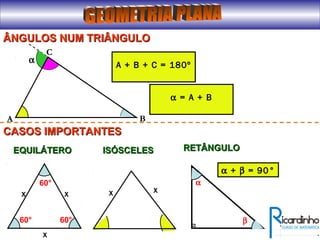
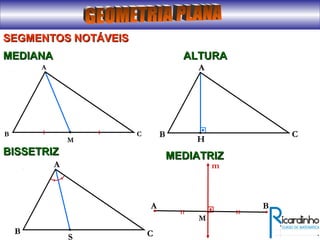
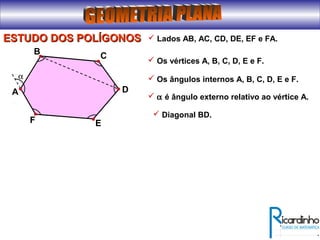
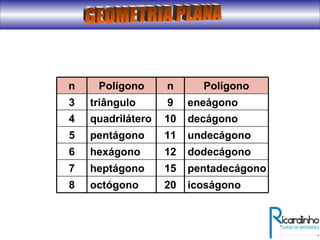
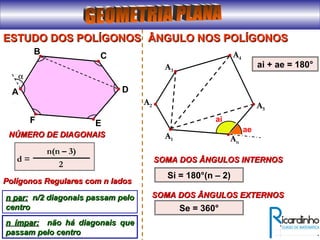
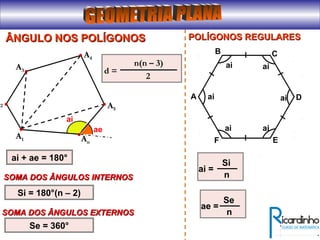
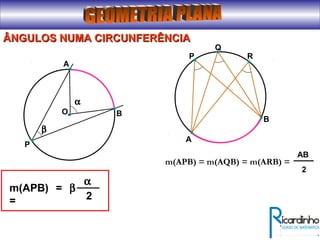
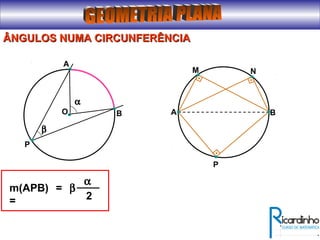
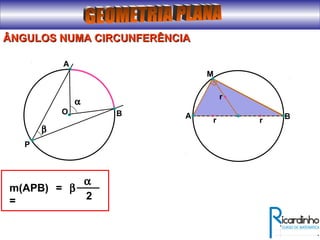
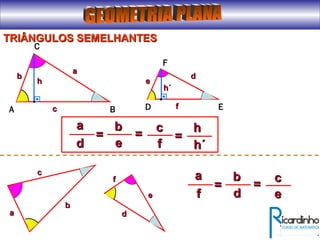
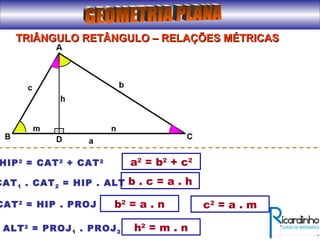
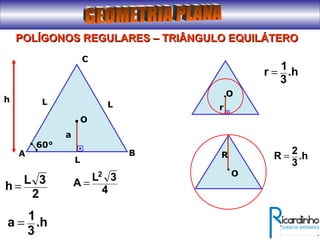
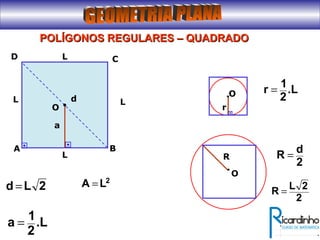
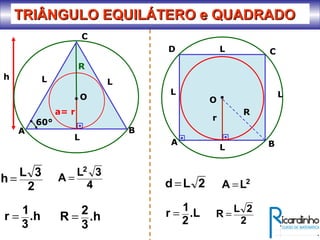
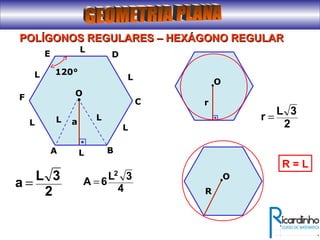
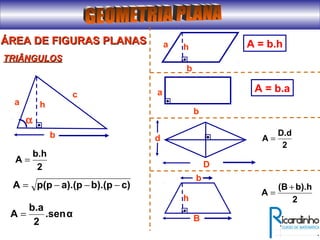
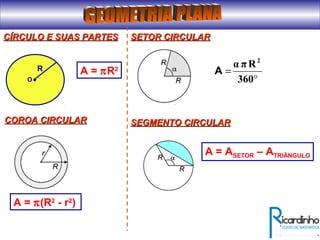
O documento fornece informações sobre ângulos e figuras planas da geometria euclidiana. Apresenta definições de ângulos, classificação de ângulos, teoremas sobre ângulos em triângulos e entre paralelas, propriedades de segmentos notáveis em triângulos, definições e propriedades de polígonos regulares e cálculo de áreas de figuras planas como triângulos, círculos e suas partes.

2. O
A
B
O → vértice do ângulo
AO e OB lados do ângulo
α
Ângulo AÔB = α
ÂNGULOSÂNGULOS
O
A
B
AGUDO
0º < α < 90ºα
ÂNGULOS - CLASSIFICAÇÃOÂNGULOS - CLASSIFICAÇÃO
O
A
B
RETO
m(AÔB) = 90º
OBTUSO
90º < β < 180º
O
A
B
β

3. 2 ÂNGULOS PODEM SER:2 ÂNGULOS PODEM SER:
O
β
α + β = 90º
α
COMPLEMENTARES SUPLEMENTARES REPLEMENTARES
O
α
α + β = 180º
β
O
α
β
α + β = 360º
x°
80°
30°
SuplementoComplemento Replemento
60° 150° 330°
10° 100° 280°
90° - x 180° - x 360° - x

4. ÂNGULOS ENTRE PARALELASÂNGULOS ENTRE PARALELAS
r
s
t
1
2
34
5
6
78

5. ÂNGULOS ENTRE PARALELASÂNGULOS ENTRE PARALELAS
r
s
t
β α
α
α
α
β
β
β
α + β = 180º
a
b
2x –
10º
3x +
40º
a//b
3x +
40º
3x + 40 + 2x – 10 = 180
5x + 30 = 180
5x = 150
x = 30º

6. ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
A
C
B
A + B + C = 180º

7. A
C
B
β
r
α
A + B + C = 180º
α + β + θ = 180°
⇒
r // AB
α β
θ

8. ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
A
C
B
A + B + C = 180º
TEOREMA DO ÂNGULO EXTERNOTEOREMA DO ÂNGULO EXTERNO
α
A
C
B
α = A + B

9. f
A
C
B
e = A + B
g
e
f = A + C
g = B + C
ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
A
C
B
A + B + C = 180º
TEOREMA DO ÂNGULO EXTERNOTEOREMA DO ÂNGULO EXTERNO

10. B
A
D
76º 115º
C
x
y y
76 + y = 115 y = 39º⇒
115 + y = x
115 + 39 = x
x = 154º⇒
Exemplo
• Na figura abaixo, AC é bissetriz interna do triângulo ABD.
Calcular a medida x do ângulo indicado.

11. ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
A + B + C = 180º
α
A
C
B
α = A + B
CASOS IMPORTANTESCASOS IMPORTANTES
xx
x
60°
60°
60°
EQUILÁTEROEQUILÁTERO ISÓSCELESISÓSCELES
xx
RETÂNGULORETÂNGULO
α
β
α + β = 90°

12. SEGMENTOS NOTÁVEISSEGMENTOS NOTÁVEIS
B
A
C
M
MEDIANAMEDIANA ALTURAALTURA
B
A
C
H
BISSETRIZBISSETRIZ
B
A
CS
MEDIATRIZMEDIATRIZ
A
m
B
M

13. ESTUDO DOS POLÍGONOSESTUDO DOS POLÍGONOS  Lados AB, AC, CD, DE, EF e FA.
 Os vértices A, B, C, D, E e F.
 Os ângulos internos A, B, C, D, E e F.
 α é ângulo externo relativo ao vértice A.
 Diagonal BD.
A
B C
D
EF
α

14. icoságono20octógono8
pentadecágono15heptágono7
dodecágono12hexágono6
undecágono11pentágono5
decágono10quadrilátero4
eneágono9triângulo3
PolígononPolígonon

15. ESTUDO DOS POLÍGONOSESTUDO DOS POLÍGONOS
A
B C
D
EF
α
d =
n(n – 3)
2
NÚMERO DE DIAGONAISNÚMERO DE DIAGONAIS
Polígonos Regulares com n ladosPolígonos Regulares com n lados
n par:n par: n/2 diagonais passam pelon/2 diagonais passam pelo
centrocentro
n ímpar:n ímpar: não há diagonais quenão há diagonais que
passam pelo centropassam pelo centro
ÂNGULO NOS POLÍGONOSÂNGULO NOS POLÍGONOS
A2
A3
A4
A5
An
A1
SOMA DOS ÂNGULOS INTERNOSSOMA DOS ÂNGULOS INTERNOS
Si = 180°(n – 2)
SOMA DOS ÂNGULOS EXTERNOSSOMA DOS ÂNGULOS EXTERNOS
Se = 360°
ai + ae = 180°
ai
ae

16. ÂNGULO NOS POLÍGONOSÂNGULO NOS POLÍGONOS
A2
A3
A4
A5
An
A1
SOMA DOS ÂNGULOS INTERNOSSOMA DOS ÂNGULOS INTERNOS
Si = 180°(n – 2)
SOMA DOS ÂNGULOS EXTERNOSSOMA DOS ÂNGULOS EXTERNOS
Se = 360°
ai + ae = 180°
ai
ae
d =
n(n – 3)
2
POLÍGONOS REGULARESPOLÍGONOS REGULARES
B
A
C
D
EF
ai
ai
ai ai
ai
ai
ai =
Si
n
ae =
Se
n

17. ÂNGULOS NUMA CIRCUNFERÊNCIAÂNGULOS NUMA CIRCUNFERÊNCIA
O
A
B
ββ
P
αα
m(APB) = β
=
α
2
P
A
B
Q
R
m(APB) = m(AQB) = m(ARB) =
AB
2

18. ÂNGULOS NUMA CIRCUNFERÊNCIAÂNGULOS NUMA CIRCUNFERÊNCIA
O
A
B
ββ
P
αα
m(APB) = β
=
α
2
M
A B
P
N

19. ÂNGULOS NUMA CIRCUNFERÊNCIAÂNGULOS NUMA CIRCUNFERÊNCIA
O
A
B
ββ
P
αα
m(APB) = β
=
α
2
M
A Br r
r

20. TRIÂNGULOS SEMELHANTESTRIÂNGULOS SEMELHANTES
A
C
B D E
F
cc
aa
bb dd
ee
ff
aa
dd
==
bb
ee
== cc
ff
hh
h´h´
==
h´h´
hh
cc
aa
bb
dd
ee
ff aa
ff
==
bb
dd
== cc
ee

21. TRIÂNGULO RETÂNGULO – RELAÇÕES MÉTRICASTRIÂNGULO RETÂNGULO – RELAÇÕES MÉTRICAS
a2
= b2
+ c2
HIP2
= CAT2
+ CAT2
CAT1 . CAT2 = HIP . ALT b . c = a . h
CAT2
= HIP . PROJ b2
= a . n
ALT2
= PROJ1 . PROJ2
c2
= a . m
h2
= m . n

22. POLÍGONOS REGULARES – TRIÂNGULO EQUILÁTEROPOLÍGONOS REGULARES – TRIÂNGULO EQUILÁTERO
O
A B
a
L
C
LLh
60°
4
3L
A
2
=
2
3L
h =
.h
3
1
a =
.h
3
1
r =
.h
3
2
R =
O
r
O
R

23. POLÍGONOS REGULARES – QUADRADOPOLÍGONOS REGULARES – QUADRADO
2
LA =2Ld =
.L
2
1
a =
O
A B
a
d
L
CD
L
L
L
.L
2
1
r =
2
2L
R =
O
r
O
R
2
d
R =

24. TRIÂNGULO EQUILÁTERO e QUADRADOTRIÂNGULO EQUILÁTERO e QUADRADO
O
A B
a= r
L
C
LLh
60°
4
3L
A
2
=
2
3L
h =
R
.h
3
1
r = .h
3
2
R =
2
LA =2Ld =
O
A B
r
R
L
CD
L
L
L
.L
2
1
r =
2
2L
R =

25. O
a
LA B
POLÍGONOS REGULARES – HEXÁGONO REGULARPOLÍGONOS REGULARES – HEXÁGONO REGULAR
C
DE
F
L
L
L
L
L
120°
LL
2
3L
a =
2
3L
r =
O
r
4
3L
6A
2
=
4
3L
6.A
2
=
O
R
R = L

26. ÁREA DE FIGURAS PLANASÁREA DE FIGURAS PLANAS
b
h
2
b.h
A =
c)b).(pa).(pp(pA −−−=
α.sen
2
b.a
A =
a
c
α
b
TRIÂNGULOSTRIÂNGULOS
h A = b.ha
b
a A = b.a
D
d
2
D.d
A =
2
b).h(B
A
+
=
B
b
h

27. CÍRCULO E SUAS PARTESCÍRCULO E SUAS PARTES
O
R A = πR2
COROA CIRCULARCOROA CIRCULAR
A = π(R2
- r2
)
SETOR CIRCULARSETOR CIRCULAR
°
=
360
Rπα 2
A
SEGMENTO CIRCULARSEGMENTO CIRCULAR
A = ASETOR – ATRIÂNGULO