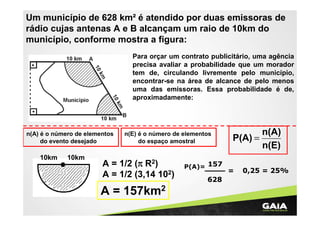
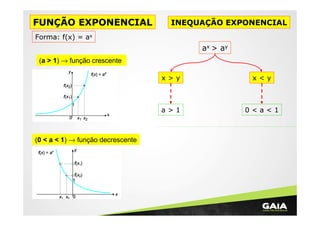
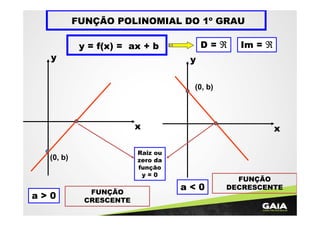
O documento apresenta informações sobre funções polinomiais do 1o grau e suas características gráficas. Em menos de 3 frases: O documento discute funções polinomiais do 1o grau, definindo-as como y=ax+b e apresentando suas formas gráficas de acordo com os valores de a, podendo ser crescentes ou decrescentes. Além disso, aborda conceitos como raiz, domínio e imagem dessas funções.

1. RICARDINHO

2. FUNÇÕES

3. FUNÇÃO POLINOMIAL DO 1º GRAU
D=ℜ
y = f(x) = ax + b
y
Im = ℜ
y
(0, b)
x
Raiz ou
zero da
função
y=0
(0, b)
a>0
x
FUNÇÃO
CRESCENTE
a<0
FUNÇÃO
DECRESCENTE

4. Lembrando....
y = ax2 + bx + c
a>0
a<0
x1
yV
−b
xV =
2a
Vértice
e
−∆
yV =
4a
ou
x1 = x2
∆<0
x2
x1 ≠ x2
∆=0
xV
Côncava para
baixo
∆>0
c
Côncava para
cima
não há raízes
reais
x1 + x 2
xV =
e yV = f ( xV )
2

5. RESUMO GRÁFICO
∆>0
∆=0
x1 ≠ x2
∆<0
x1 = x2
x1, x2 ∉ R
y
y
x1
x2
x
y
x1 = x2
x
x

6. +1
Sejam as funções f(x) = 2x− 4 definida para todo x
x
real e x ≠ 4, g(x) = x + 3 e h(x) = 2x2 – 12x + 16
definida para todo x real. Determine a soma dos
números
associados
à(s)
proposição(ões)
VERDADEIRA(S).

7. f(x) = 2x +1
x −4
g(x) = x + 3
h(x) = 2x2 – 12x + 16
01. O domínio da função k(x) = h(x) é definido por
D(h) = {x ∈ ℜ/ 2 ≤ x ≤ 4}
k(x)= h(x)
k(x) = 2x2 −12x +16
D(h) { x ∈ R | x ≤ 2 ou x ≥ 5}
LSO
FA
02. A função h(x) é par.
SO
AL
F
2x2 – 12x + 16 ≥ 0
x2 – 6x + 8 ≥ 0
+
+
2
_
4

8. f(x) = 2x +1
x −4
g(x) = x + 3
h(x) = 2x2 – 12x + 16
04. O valor de f(g(2)) é igual a 11.
f(x) = 2x +1
x −4
f(5) = 2.5+1
5−4
f(5) = 11
08.
f(x) = 2x +1
x −4
IRO
DE
DA
ER
V
g(x) = x + 3
IRO
g(2) = 2 + 3
DE
DA
ER
g(2) =5
V
f-1(x) = 4x +1
x −2

9. f(x) = 2x +1
x −4
g(x) = x + 3
h(x) = 2x2 – 12x + 16
16. A reta que representa a função g intercepta o eixo das
abscissas em (1,0)
y
Raiz ou
zero da
função
y=0
g(x) = x + 3
SO
AL
F
(0, 3)
b)
(-3,0)
x
32. A função f assume valores estritamente positivos para
x < -1/2 ou x > 4
IRO
DE
DA
ER
V

10. f(x) = 2x +1
x −4
h(x) = 2x2 – 12x + 16
g(x) = x + 3
64. O valor mínimo de h(x) é – 1.
y
h(x) = 2x2 – 12x + 16
−b
− (−12)
∴V =
x
xV =
2a
2.2
xV = 3
(0,16)
3
x1
-2
x2
Vértice
x
h(3) = 2.(3)2 – 12.3 + 16
h(3) = - 2

11. EXPONENCIAL e
LOGARITMOS

12. log 2x + log (1 + 2x) = log 6
log 2x + log (1 + 2x) = log 6
log [(2x (1 + 2x)] = log 6
2x (1 + 2x) = 6
y (1 + y) = 6
y + y2 = 6
y2 + y – 6 = 0
y’ = 2
y’’ = - 3
Incógnita auxiliar:
2X = y
2x = 2
x=1

13. FUNÇÃO EXPONENCIAL
INEQUAÇÃO EXPONENCIAL
Forma: f(x) = ax
ax > ay
(a > 1) → função crescente
x>y
a>1
(0 < a < 1) → função decrescente
x<y
0<a<1

14. Função Logarítmica
Definição
logB A = x ↔ A = Bx
A>0
y
y = loga x
a>1
1≠B>0
Casos Particulares
logB 1 = 0 logA A = 1
logA Am = m
x
0
1
Propriedades
logC (A.B) = logc A + logc B
logC (A/B) = logc A – logc B
logC Am = m.logc A
MUDANÇA DE BASE
logB A =
log c A
log cB
y = loga x
0<a<1

15. Uma pessoa comprou um imóvel com intenção de investir
seu dinheiro. Sabendo-se que este imóvel valorizou 12% ao
ano, determine:
a) Dados: log 2 = 0,30 e log 7 = 0,84. Determine o valor do log 1,12.
 112 
log 1,12 = log

 100 
log 1,12 = log 24 + log 7 – 2
log 1,12 = 4.0,30 + 0,84 – 2
log 1,12 = log 112 – log 100
log 1,12 = 0,04
log 1,12 = log (24.7) – log 102
b) Após quanto tempo o valor valor do imóvel duplicou?
M = C(1 + i)t
2x = x(1 + 0,12)t
2 = (1,12)t
log 2 = log (1,12)t
0,30 = t .log (1,12)
0,30 = t .0,04
t = 7,5 (7 anos e 6 meses)

16. PROGRESSÕES

17. P. A.
a1, a2, a3, ……., an
CONDIÇÃO DE EXISTÊNCIA:
a2 – a1 = a 3 – a2 = r
TERMO GERAL
P. G.
a1, a2, a3, ……., an
RAZÃO DA P.G.
a2 a3
=
= ... = q
a1 a 2
TERMO GERAL
a2 = a1 + r
a2 = a1 . q
a3 = a1 + 2r
a3 = a1 . q2
a4 = a1 + 3r
a4 = a1 . q3
an = a1 + (n – 1).r
SOMA DOS TERMOS
an = a1 . q n – 1
SOMA DOS TERMOS
Sn = (a1 + an). n
2
3 TERMOS EM P.G.
x
; x; xq
q
a 1 .(qn − 1)
Sn =
q−1
limite S ∞ =
a1
1- q

18. PROGRESSÕES: ASSINALE V ou F
A sequência (1 – 3x, x – 2, 2x + 1) é uma P.A e a sequência
(1 + y, 13 + y, 49 +y) é uma P.G, então o valor de x.y é 10.
P.A
P.G
a2 – a1 = a3 – a2
a2
a1
x – 2 – (1 – 3x) = 2x + 1 – (x – 2)
4x – 3 = x + 3
x=2
=
a3
a2
13+ y = 49 + y
1+y
13 + y
(13 + y)2 = (1 + y).(49 + y)
VERDADEIRO
y=5

19. PROGRESSÕES: ASSINALE V ou F
A soma dos números ímpares de 27 a 75 é 1275.
27
75
Sn =
( a1 + an) · n
2
a1
an
S25 =
( a1 + a25) · 25
2
an = a1 + (n – 1)r
75 = 27 + (n – 1).2
n = 25
VERDADEIRO
S25 =
( 27 + 75) · 25
2
S25 = 1275

20. PROGRESSÕES: ASSINALE V ou F
A soma dos termos da P.G (3-1, 3-2, 3-3, ...........) é 1
(3-1 + 3-2 + 3-3 + ……..)
1 1
1 + .... 
 +

+


3 9 27


a1
S∞ =
1- q
0 < |q| < 1
1
3
S=
1− 1
3
S = 0,5
Falso

21. MATRIZ INVERSA

22. MATRIZ INVERSA
A . A-1 = In
detA −1
1
=
detA
a b
A=
 c d



2 1
A=
 7 5



det A =3
• Se det A ≠ 0 a matriz possui inversa,
sendo assim chamada de inversível.
• Se det A = 0 a matriz não admite
inversa é chamada de singular.
- 1 =  d − b

A
− c a 



 d

A - 1 =  det A
 -c
 det A

- 1 =  5 − 1

A
− 7 2 



 5

A- 1 =  3
-7

 3
-b 

det A 
a 
det A 

-1

3
2

3

23. LEMBRAR !!!!!!
det(A.B) = detA.det B
(Teorema de Binet)
CUIDADO: det(A + B) ≠ detA + det B
vale lembrar que:
k ∈ R, n é a ordem da matriz
det (k.A) = kn. det A

24. GEOMETRIA
ANALÍTICA

25. y
ESTUDO DA RETA
r
B
yB
FORMAS DE OBTENÇÃO
Dados 2 pontos
x
xA
xB
y
yA
yB
1
1=0
1
y – yo = m(x – xo)
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
EQUAÇÃO REDUZIDA
ax + by + c = 0
y = mx + n
Coef.
Coef.
angular linear
CÁLCULO DO COEFICIENTE ANGULAR
m = tg α
yB– yA
Dados 1 ponto e o coef. angular
m=
yB − y A
xB − x A
A
yA
α
xB– xA
α
xA
O
xB
x
(0, n)
POSIÇÕES RELATIVAS
PARALELAS: mr = ms
CONCORRENTES: mr ≠ ms
PERPENDICULARES: mr . ms = – 1

26. ESTUDO DA CIRCUNFERÊNCIA
EQUAÇÃO DA CIRCUNFERÊNCIA
y
EQUAÇÃO REDUZIDA
P
y
β
C
R
(x – α)2 + (y – β )2 = R2
y-β
x-α
EQUAÇÃO GERAL
x2 + y2 + Ax + By + C = 0
α
x
x
A = - 2α
B=-2β
÷(
)
(-2
÷
-2)
x2 + y2 – 4x – 6y + 9 = 0
β=3
α=2
C( 2 , 3 )
C = α 2 + β 2 – R2
9 = (2)2 + (3)2 – R2
R=2
C = α2 + β2 – R2

27. PORCENTAGEM

28. AUMENTOS E DESCONTOS
AUMENTAR O PREÇO DE UMA MERCADORIA EM 20%
SIGNIFICA MULTIPLICAR SEU VALOR POR: 1,2
AUMENTAR O PREÇO DE UMA MERCADORIA EM 2%
SIGNIFICA MULTIPLICAR SEU VALOR POR: 1,02
DIMINUIR O PREÇO DE UMA MERCADORIA EM 20%
SIGNIFICA MULTIPLICAR SEU VALOR POR:
0,8
Aumento sucessivo de 10% e 20% no preço de um
determinado produto é equivalente a um único aumento de:
1,1 . 1,2 = 1,32
32%

29. Quando chegou o inverno, um comerciante aumentou em
10% o preço de cada jaqueta de couro do seu estoque.
Terminada a estação, fez uma promoção com 20% de
desconto, passando o preço da jaqueta para R$ 176,00. O
preço inicial de cada jaqueta, antes do aumento, era:
PREÇO INICIAL:x
1,1
0,8
x
= 176
0,88x = 176
x = 200

30. Se um cubo tem as suas arestas aumentadas em 20% cada
uma, então o seu volume fica aumentado em:
1,2 a
a
1,2 a
a
1,2 a
a
V
=1 a3
V = (1,2a)3
V = 1,728a3
Portanto, o volume aumentado
em 72,8%

31. Um município de 628 km² é atendido por duas emissoras de
rádio cujas antenas A e B alcançam um raio de 10km do
município, conforme mostra a figura:
Para orçar um contrato publicitário, uma agência
precisa avaliar a probabilidade que um morador
tem de, circulando livremente pelo município,
encontrar-se na área de alcance de pelo menos
uma das emissoras. Essa probabilidade é de,
aproximadamente:
n(A) é o número de elementos
do evento desejado
10km
10km
n(E) é o número de elementos
do espaço amostral
A = 1/2 (π R2)
π
A = 1/2 (3,14 102)
A = 157km2
P(A)= 157
628
n(A)
P(A) =
n(E)
=
0,25 = 25%