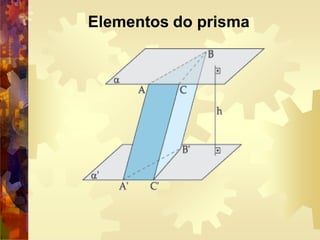
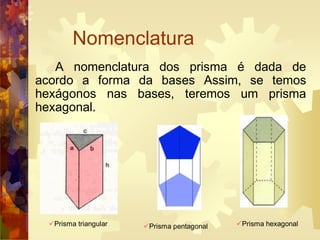
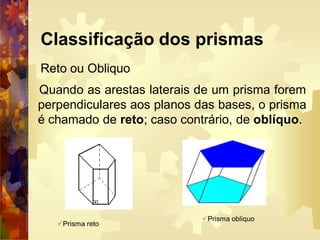
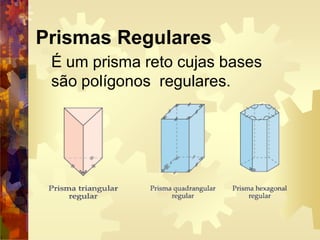
Um prisma é um poliedro com duas faces paralelas iguais chamadas de bases e faces laterais em forma de paralelogramos. Há diferentes tipos de prisma nomeados de acordo com a forma da base, como prisma triangular, pentagonal ou hexagonal. Prismas podem ser retos, com arestas perpendiculares às bases, ou oblíquos. O volume de um prisma é calculado multiplicando a área da base pela altura.