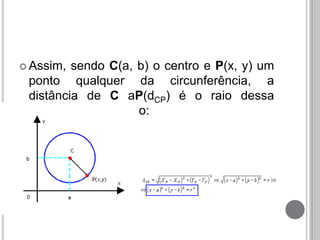
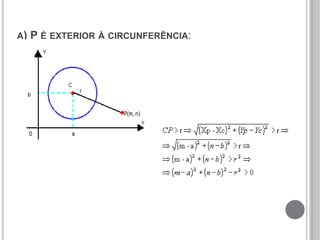
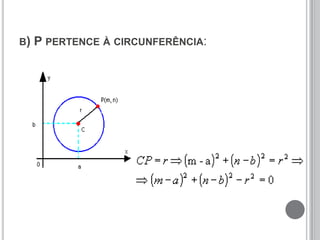
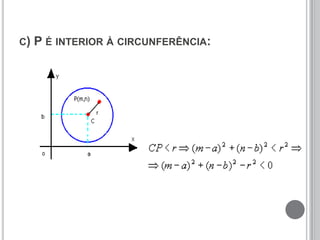
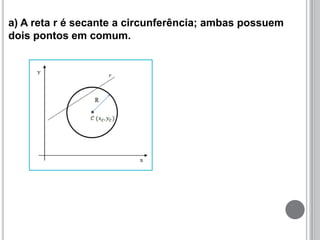
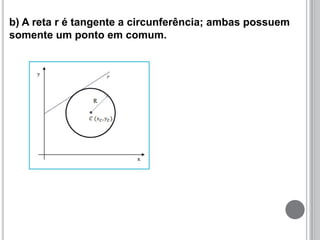
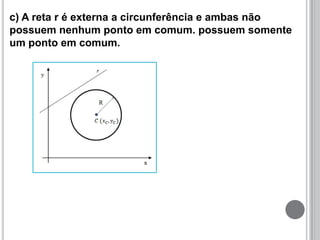
O documento discute a definição de circunferência e sua equação reduzida. Apresenta as posições relativas entre pontos, retas e circunferências, como secante, tangente e externa. Também explica as posições relativas entre duas circunferências, como tangentes, secantes, externas, internas ou concêntricas. Por fim, fornece exemplos para ilustrar os conceitos.

1. ESTUDO DA CIRCUNFERÊNCIA
3 Edificações
Grupo 4

2. INSTITUTO FEDERAL DE SERGIPE (CAMPUS
LAGARTO)
 Alunos:
Andréa Neto;
Cristian Valéria;
Fernanda Lopes;
Hortência Santana;
Joana Sueveny;
Laísa Fraga;
Larissa Menezes;
Luciana Venceslau;
Natalia Ramos.

3. DEFINIÇÃO:
Equação reduzida da Circunferência
Circunferência é o conjunto de todos os pontos de
um plano eqüidistantes de um ponto fixo, desse
mesmo plano, denominado centro da
circunferência:

4.  Assim, sendo C(a, b) o centro e P(x, y) um
ponto qualquer da circunferência, a
distância de C aP(dCP) é o raio dessa
circunferência. Então:

5.  Portanto, (x - a)2 + (y - b)2 =r2 é a equação
reduzida da circunferência e permite
determinar os elementos essenciais para a
construção da circunferência: as
coordenadas do centro e o raio.
 Observação: Quando o centro da
circunfer6encia estiver na origem (
C(0,0)), a equação da circunferência
será x2 + y2 = r2 .

6. EQUAÇÃO GERAL DA CIRCUNFERÊNCIA
 Desenvolvendo a equação
reduzida, obtemos a equação geral da
circunferência:

7. POSIÇÕES RELATIVAS ENTRE PONTO E
CIRCUNFERÊNCIA
 Em relação à circunferência de equação ( x
- a )2 + ( y - b )2 = r2, o ponto P(m, n) pode
ocupar as seguintes posições:

8. A) P É EXTERIOR À CIRCUNFERÊNCIA:

9. B) P PERTENCE À CIRCUNFERÊNCIA:

10. C) P É INTERIOR À CIRCUNFERÊNCIA:

11. 
Assim, para determinar a posição de um
ponto P(m, n) em relação a uma
circunferência, basta substituir as
coordenadas de P na expressão
( x - a )2 + ( y - b )2 - r2 .

12. Posição relativa entre ponto e reta e
circunferência:
 Existem três posições possíveis entre uma
circunferência e uma reta no plano:

13. a) A reta r é secante a circunferência; ambas possuem
dois pontos em comum.

14. b) A reta r é tangente a circunferência; ambas possuem
somente um ponto em comum.

15. c) A reta r é externa a circunferência e ambas não
possuem nenhum ponto em comum. possuem somente
um ponto em comum.

16. Utilizando-se a fórmula da distância entre um ponto e
uma reta, adaptado para a distância entre o centro da
circunferência e a reta r de equação geralax + by + c =
0:
Podemos concluir a posição relativa entre a reta e a circunferência a partir dos
seguintes dados:
a) se d < R a reta é secante à circunferência.
b) se d = R a reta é tangente à circunferência.
c) se d > R a reta é externa à circunferência.

17. Posição relativa entre ponto e circunferência
Utilizando-se o mesmo raciocínio do item anterior determina-se a
distância entre o ponto P(xp, yp) e o centro da circunferência por
intermédio da fórmula:
•Se d > R o ponto é externo à
circunferência.
•Se d = R o ponto pertence à
circunferência.
• Se d o ponto é interno à
circunferência.

18. Posição relativa entre duas circunferências:
No estudo analítico da circunferência, os elementos
raio, diâmetro e centro da circunferência são
fundamentais para conclusões de diversos
problemas e para a determinação da equação que
define essa forma geométrica tão importante. Em se
tratando de posições relativas entre duas
circunferências, elas podem ser:
tangentes, secantes, externas, internas ou
concêntricas. Vamos analisar cada caso.

19. Circunferências tangentes.

20. a) Tangentes externas
Duas circunferências são tangentes internas
quando possuem somente um ponto em comum
e uma exterior à outra. A condição para que isso
ocorra é que a distância entre os centros das
duas circunferências seja equivalente à soma
das medidas de seus raios.
dOC = r1 + r2

21. b) Tangentes internas
Duas circunferências são tangentes internas
quando possuem apenas um ponto em comum e
uma esteja no interior da outra. A condição para
que isso ocorra é que a distância entre os dois
centros seja igual à diferença entre os dois raios.
dOC = r1 - r2

22. Circunferências externas.
Duas circunferências são consideradas
externas quando não possuem pontos em
comum. A condição para que isso ocorra é que
a distância entre os centros das
circunferências deve ser maior que a soma
das medidas de seus raios.
dOC > r1 + r2

23. Circunferências secantes.
Duas circunferências são consideradas
secantes quando possuem dois pontos em
comum. A condição para que isso aconteça é
que a distância entre os centros das
circunferências deve ser menor que a soma das
medidas de seus raios.
dCO < r1 + r2


24. Circunferências internas.
Duas circunferências são consideradas internas
quando não possuem pontos em comum e uma
está localizada no interior da outra. A condição
para que isso ocorra é que a distância entre os
centros das circunferências deve ser equivalente
à diferença entre as medidas de seus raios.
dOC < r1 - r2

25. Circunferências concêntricas.
Duas circunferências são consideradas
concêntricas quando possuem o centro em
comum. Nesse caso, a distância entre os centro
é nula.
dCO = 0

26. AGORA VEJAMOS ALGUNS EXEMPLOS:

27. EXEMPLO 1:
 Determine a equação da circunferência com
centro no ponto C(4;7) e raio R=2.

28. EXEMPLO 2:
 Determine a equação da circunferência com
centro no ponto C(2;3) e que passa pelo
ponto P(-1;2).

29. EXEMPLO 3:
 Ache a equação da circunferência cujas
extremidades de mm diâmetro são os
pontos
A(0;-8) e B(6;0).

30. REFERÊNCIAS:
 http://www.brasilescola.com/matematica/circ
unferencia.htm
 https://sites.google.com/site/geometriaanaliti
caportifolio/calendar
 http://mscabral.pro.br/sitemauro/aulas/circul
o.htm