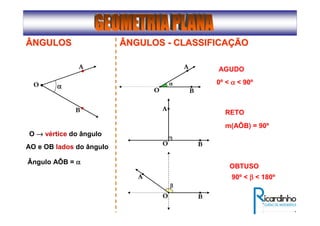
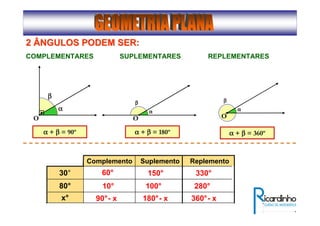
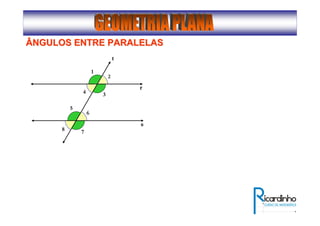
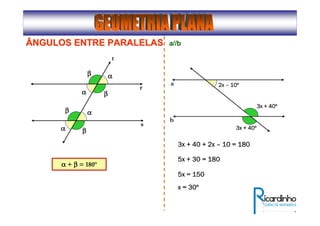
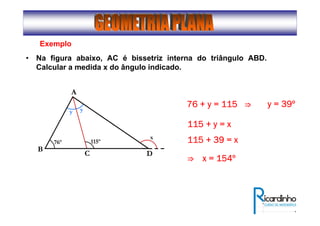
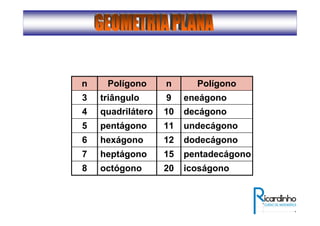
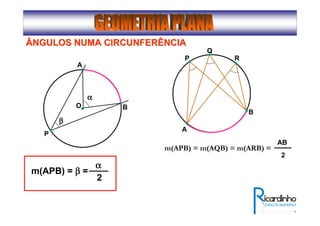
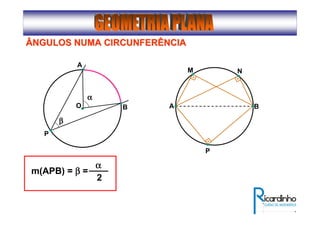
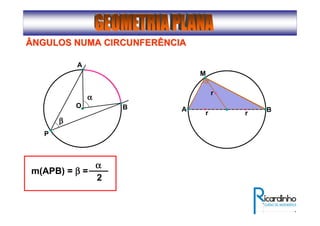
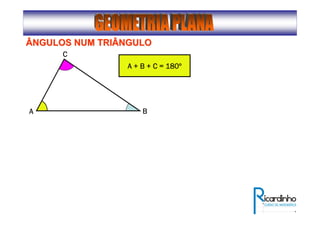
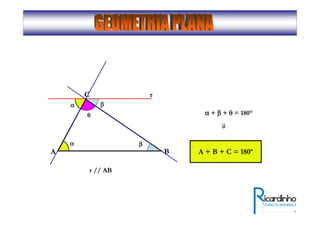
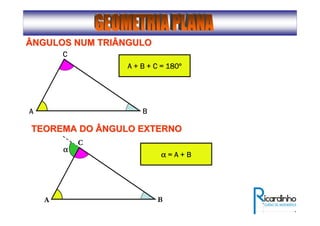
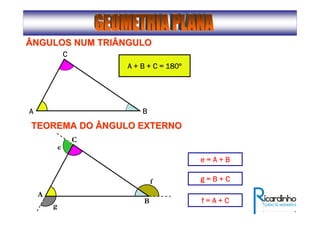
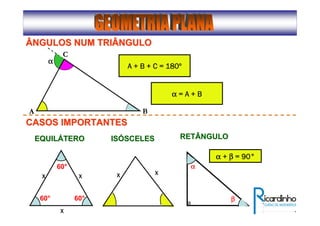
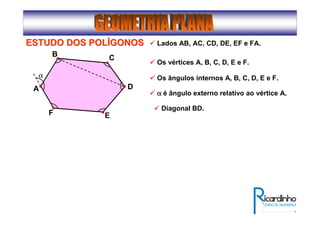
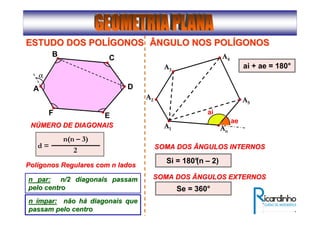
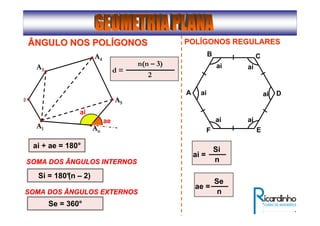
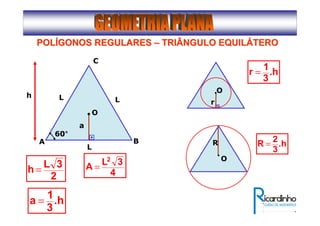
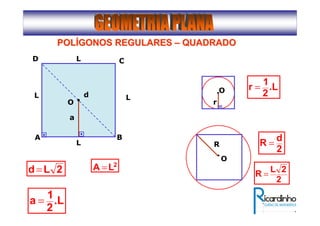
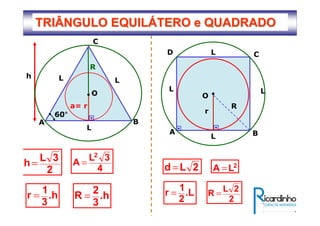
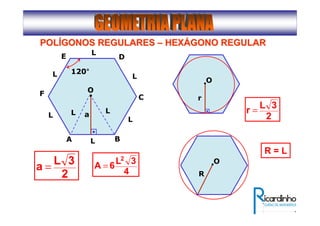
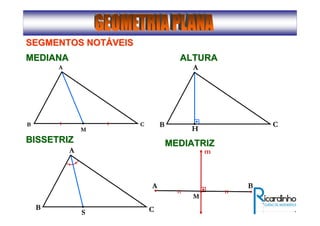
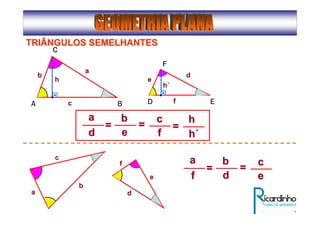
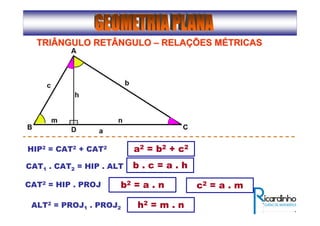
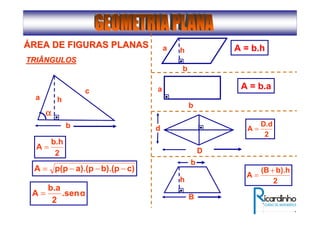
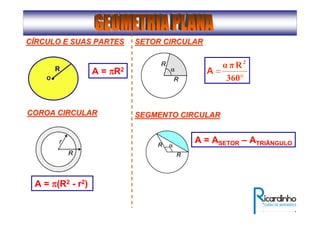
1) O documento descreve conceitos básicos de ângulos e classificação de ângulos; 2) Apresenta os tipos de ângulos em triângulos e polígonos regulares e suas propriedades; 3) Discutem segmentos notáveis em triângulos e áreas de figuras planas como triângulos, círculos e suas partes.

2. O
A
B
O →→→→ vértice do ângulo
AO e OB lados do ângulo
αααα
Ângulo AÔB = αααα
ÂNGULOSÂNGULOS
O
A
B
AGUDO
0º < αααα < 90ºαααα
ÂNGULOSÂNGULOS -- CLASSIFICACLASSIFICAÇÇÃOÃO
O
A
B
RETO
m(AÔB) = 90º
OBTUSO
90º < ββββ < 180º
O
A
B
ββββ

3. 2 ÂNGULOS PODEM SER:2 ÂNGULOS PODEM SER:
O
ββββ
αααα + ββββ = 90º
αααα
COMPLEMENTARES SUPLEMENTARES REPLEMENTARES
O
αααα
αααα + ββββ = 180º
ββββ
O
αααα
ββββ
αααα + ββββ = 360º
x°
80°
30°
SuplementoComplemento Replemento
60° 150° 330°
10° 100° 280°
90°- x 180°- x 360°- x

4. ÂNGULOS ENTRE PARALELASÂNGULOS ENTRE PARALELAS
r
s
t
1
2
34
5
6
78

5. ÂNGULOS ENTRE PARALELASÂNGULOS ENTRE PARALELAS
r
s
t
ββββ αααα
αααα
αααα
αααα
ββββ
ββββ
ββββ
αααα + ββββ = 180º
a
b
2x2x2x2x –––– 10101010ºººº
3x + 403x + 403x + 403x + 40ºººº
a//b
3x + 403x + 403x + 403x + 40ºººº
3x + 40 + 2x3x + 40 + 2x3x + 40 + 2x3x + 40 + 2x –––– 10 = 18010 = 18010 = 18010 = 180
5x + 30 = 1805x + 30 = 1805x + 30 = 1805x + 30 = 180
5x = 1505x = 1505x = 1505x = 150
x = 30x = 30x = 30x = 30ºººº

6. ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
AAAA
CCCC
BBBB
A + B + C = 180A + B + C = 180A + B + C = 180A + B + C = 180ºººº

7. A
C
B
ββββ
r
αααα
A + B + C = 180º
αααα + ββββ + θθθθ = 180°
⇒⇒⇒⇒
r // AB
αααα ββββ
θθθθ

8. ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
AAAA
CCCC
BBBB
A + B + C = 180A + B + C = 180A + B + C = 180A + B + C = 180ºººº
TEOREMA DO ÂNGULO EXTERNOTEOREMA DO ÂNGULO EXTERNO
αααα
A
C
B
αααα ==== AAAA ++++ BBBB

9. f
A
C
B
e = A + Be = A + Be = A + Be = A + B
g
e
f = A + Cf = A + Cf = A + Cf = A + C
g = B + Cg = B + Cg = B + Cg = B + C
ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
AAAA
CCCC
BBBB
A + B + C = 180A + B + C = 180A + B + C = 180A + B + C = 180ºººº
TEOREMA DO ÂNGULO EXTERNOTEOREMA DO ÂNGULO EXTERNO

10. B
A
D
76º 115º
C
x
y y
76 + y = 11576 + y = 11576 + y = 11576 + y = 115 y = 39y = 39y = 39y = 39ºººº⇒⇒⇒⇒
115 + y = x115 + y = x115 + y = x115 + y = x
115 + 39 = x115 + 39 = x115 + 39 = x115 + 39 = x
x = 154x = 154x = 154x = 154ºººº⇒⇒⇒⇒
Exemplo
• Na figura abaixo, AC é bissetriz interna do triângulo ABD.
Calcular a medida x do ângulo indicado.

11. ÂNGULOS NUM TRIÂNGULOÂNGULOS NUM TRIÂNGULO
A + B + C = 180A + B + C = 180A + B + C = 180A + B + C = 180ºººº
αααα
A
C
B
αααα ==== AAAA ++++ BBBB
CASOS IMPORTANTESCASOS IMPORTANTES
xxxxxxxx
xxxx
60°
60°
60°
EQUILEQUILÁÁTEROTERO ISISÓÓSCELESSCELES
xxxxxxxx
RETÂNGULORETÂNGULO
αααα
ββββ
αααα ++++ ββββ = 90= 90= 90= 90°°°°

12. SEGMENTOS NOTSEGMENTOS NOTÁÁVEISVEIS
B
A
C
M
MEDIANAMEDIANA ALTURAALTURA
B
A
C
H
BISSETRIZBISSETRIZ
B
A
CS
MEDIATRIZMEDIATRIZ
A
m
B
M

13. ESTUDO DOS POLESTUDO DOS POLÍÍGONOSGONOS Lados AB, AC, CD, DE, EF e FA.
Os vértices A, B, C, D, E e F.
Os ângulos internos A, B, C, D, E e F.
αααα é ângulo externo relativo ao vértice A.
Diagonal BD.
A
B C
D
EF
α

14. icoságono20octógono8
pentadecágono15heptágono7
dodecágono12hexágono6
undecágono11pentágono5
decágono10quadrilátero4
eneágono9triângulo3
PolígononPolígonon

15. ESTUDO DOS POLESTUDO DOS POLÍÍGONOSGONOS
A
B C
D
EF
α
d =
n(n – 3)
2
NNÚÚMERO DE DIAGONAISMERO DE DIAGONAIS
PolPolíígonos Regulares com n ladosgonos Regulares com n lados
n par:n par: n/2 diagonais passamn/2 diagonais passam
pelo centropelo centro
nn íímpar:mpar: não hnão háá diagonais quediagonais que
passam pelo centropassam pelo centro
ÂNGULO NOS POLÂNGULO NOS POLÍÍGONOSGONOS
A2
A3
A4
A5
An
A1
SOMA DOS ÂNGULOS INTERNOSSOMA DOS ÂNGULOS INTERNOS
Si = 180°(n – 2)
SOMA DOS ÂNGULOS EXTERNOSSOMA DOS ÂNGULOS EXTERNOS
Se = 360°
ai + ae = 180°
ai
ae

16. ÂNGULO NOS POLÂNGULO NOS POLÍÍGONOSGONOS
A2
A3
A4
A5
An
A1
SOMA DOS ÂNGULOS INTERNOSSOMA DOS ÂNGULOS INTERNOS
Si = 180°(n – 2)
SOMA DOS ÂNGULOS EXTERNOSSOMA DOS ÂNGULOS EXTERNOS
Se = 360°
ai + ae = 180°
ai
ae
d =
n(n – 3)
2
POLPOLÍÍGONOS REGULARESGONOS REGULARES
B
A
C
D
EF
ai
ai
ai ai
ai
ai
ai =
Si
n
ae =
Se
n

17. ÂNGULOS NUMA CIRCUNFERÊNCIAÂNGULOS NUMA CIRCUNFERÊNCIA
O
A
B
ββββββββ
P
αααααααα
m(APB) = ββββ =
αααα
2
P
A
B
Q
R
m(APB) = m(AQB) = m(ARB) =
AB
2

18. ÂNGULOS NUMA CIRCUNFERÊNCIAÂNGULOS NUMA CIRCUNFERÊNCIA
O
A
B
ββββββββ
P
αααααααα
m(APB) = ββββ =
αααα
2
M
A B
P
N

19. ÂNGULOS NUMA CIRCUNFERÊNCIAÂNGULOS NUMA CIRCUNFERÊNCIA
O
A
B
ββββββββ
P
αααααααα
m(APB) = ββββ =
αααα
2
M
A Br r
r

20. TRIÂNGULOS SEMELHANTESTRIÂNGULOS SEMELHANTES
AAAA
CCCC
BBBB DDDD EEEE
FFFF
cc
aa
bb dd
ee
ff
aa
dd
==
bb
ee
== cc
ff
hh
hh´´
==
hh´´
hh
cc
aa
bb
dd
ee
ff aa
ff
==
bb
dd
== cc
ee

21. TRIÂNGULO RETÂNGULOTRIÂNGULO RETÂNGULO –– RELARELAÇÇÕES MÕES MÉÉTRICASTRICAS
a2 = b2 + c2HIP2 = CAT2 + CAT2
CAT1 . CAT2 = HIP . ALT b . c = a . h
CAT2 = HIP . PROJ b2 = a . n
ALT2 = PROJ1 . PROJ2
c2 = a . m
h2 = m . n

22. POLPOLÍÍGONOS REGULARESGONOS REGULARES –– TRIÂNGULO EQUILTRIÂNGULO EQUILÁÁTEROTERO
O
A B
a
L
C
LLh
60°°°°
4
3L
A
2
=
2
3L
h =
.h
3
1
a =
.h
3
1
r =
.h
3
2
R =
O
r
O
R

23. POLPOLÍÍGONOS REGULARESGONOS REGULARES –– QUADRADOQUADRADO
2
LA =2Ld =
.L
2
1
a =
O
A B
a
d
L
CD
L
L
L
.L
2
1
r =
2
2L
R =
O
r
O
R
2
d
R =

24. TRIÂNGULO EQUILTRIÂNGULO EQUILÁÁTERO e QUADRADOTERO e QUADRADO
O
A B
a= r
L
C
LLh
60°°°°
4
3L
A
2
=
2
3L
h =
R
.h
3
1
r = .h
3
2
R =
2
LA =2Ld =
O
A B
r
R
L
CD
L
L
L
.L
2
1
r =
2
2L
R =

25. O
a
LA B
POLPOLÍÍGONOS REGULARESGONOS REGULARES –– HEXHEXÁÁGONO REGULARGONO REGULAR
C
DE
F
L
L
L
L
L
120°°°°
LL
2
3L
a =
2
3L
r =
O
r
4
3L
6A
2
=
4
3L
6.A
2
=
O
R
R = L

26. ÁÁREA DE FIGURAS PLANASREA DE FIGURAS PLANAS
b
h
2
b.h
A =
c)b).(pa).(pp(pA −−−=
α.sen
2
b.a
A =
a
c
αααα
b
TRIÂNGULOSTRIÂNGULOS
h A = b.ha
b
a A = b.a
D
d
2
D.d
A =
2
b).h(B
A
+
=
B
b
h

27. CCÍÍRCULO E SUAS PARTESRCULO E SUAS PARTES
O
R A = ππππR2
COROA CIRCULARCOROA CIRCULAR
A = ππππ(R2 - r2)
SETOR CIRCULARSETOR CIRCULAR
°
=
360
Rπα 2
A
SEGMENTO CIRCULARSEGMENTO CIRCULAR
A = ASETOR – ATRIÂNGULO