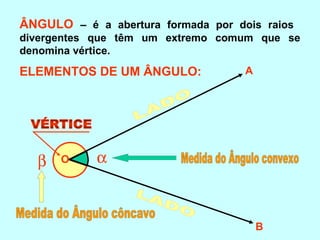
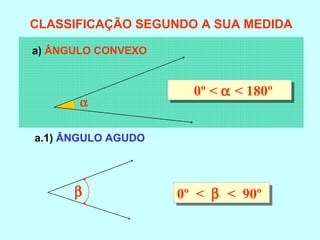
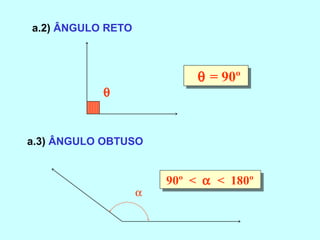
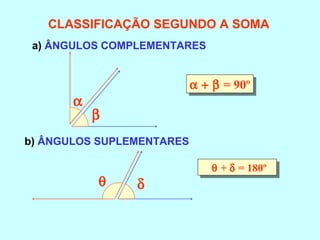
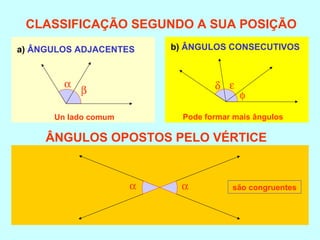
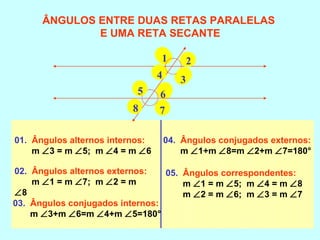
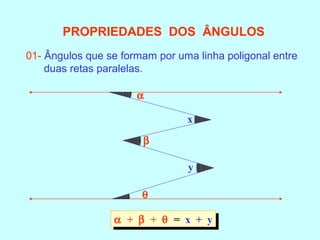
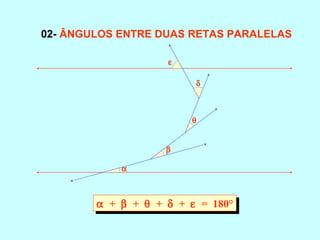
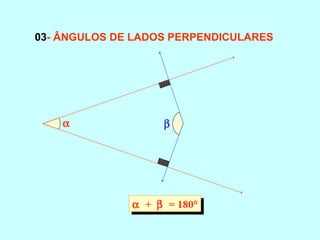
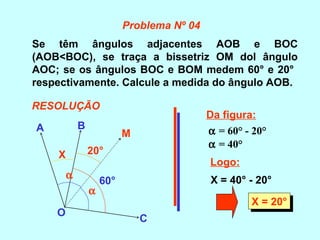
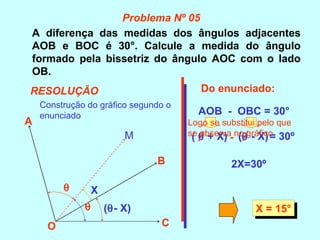
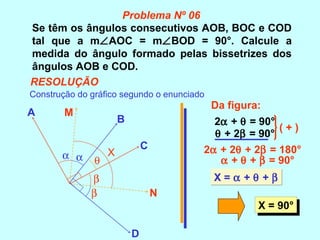
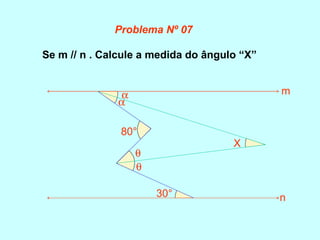
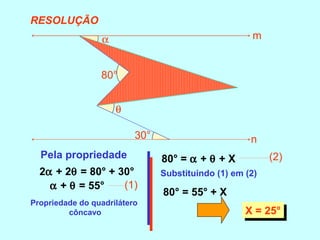
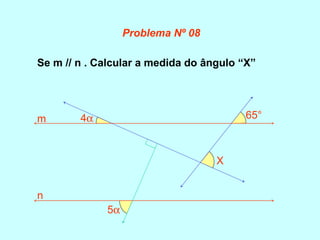
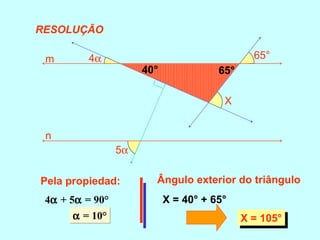
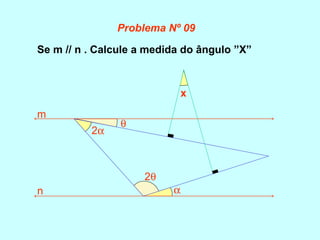
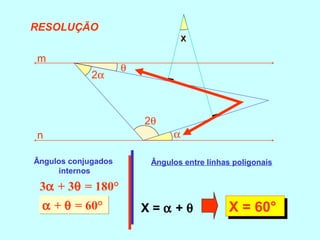
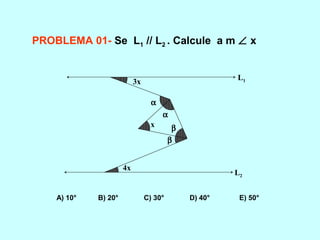
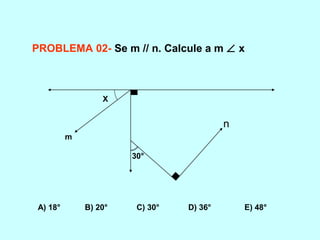
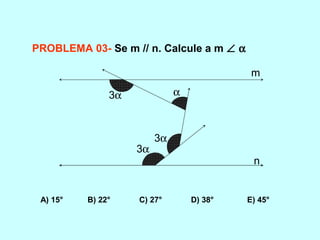
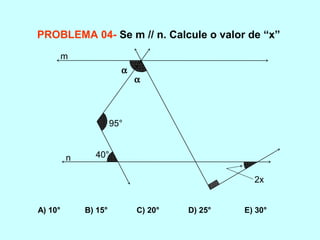
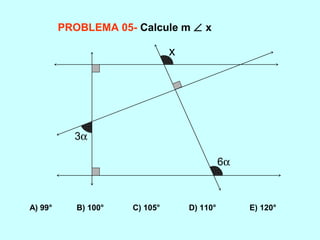
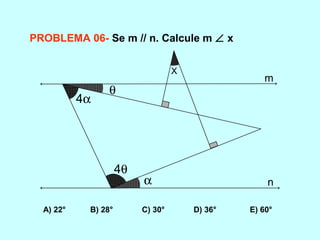
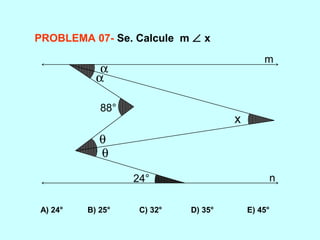
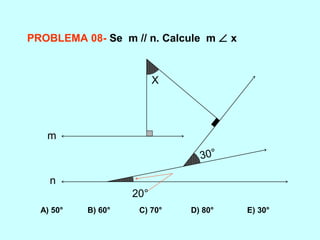
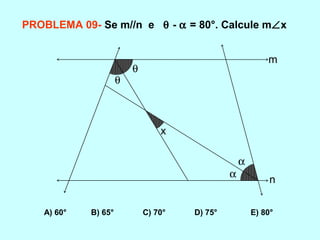
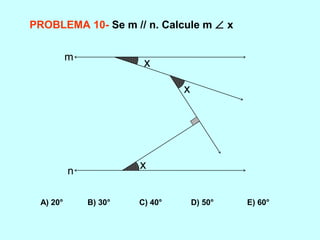
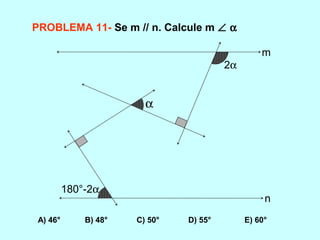
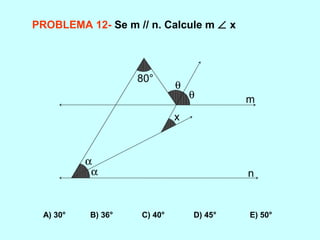
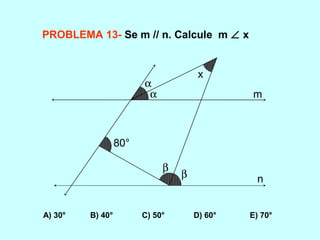
O documento discute os conceitos básicos de ângulos, incluindo sua classificação, elementos e propriedades. É apresentada a definição formal de ângulo e os tipos principais: agudo, reto e obtuso. Propriedades como ângulos adjacentes, opostos e complementares são explicadas. Por fim, vários exercícios sobre ângulos são resolvidos.

1. Ensino Superior
Matemática Básica
Unidade 11 - Ângulos
Amintas Paiva Afonso

2. β αO
A
B
ÂNGULO – é a abertura formada por dois raios
divergentes que têm um extremo comum que se
denomina vértice.
ELEMENTOS DE UM ÂNGULO:

3. α
0º < α < 180º0º < α < 180º
0º < β < 90º0º < β < 90ºβ
CLASSIFICAÇÃO SEGUNDO A SUA MEDIDA
a) ÂNGULO CONVEXO
a.1) ÂNGULO AGUDO

4. θ = 90ºθ = 90º
α
90º < α < 180º90º < α < 180º
θ
a.2) ÂNGULO RETO
a.3) ÂNGULO OBTUSO

5. α + β = 90ºα + β = 90º
θ + δ = 180ºθ + δ = 180º
δθ
α
β
CLASSIFICAÇÃO SEGUNDO A SOMA
a) ÂNGULOS COMPLEMENTARES
b) ÂNGULOS SUPLEMENTARES

6. α
β δ ε
φ
α α
CLASSIFICAÇÃO SEGUNDO A SUA POSIÇÃO
a) ÂNGULOS ADJACENTES b) ÂNGULOS CONSECUTIVOS
ÂNGULOS OPOSTOS PELO VÉRTICE
são congruentes
Pode formar mais ângulosUn lado comum

7. 01. Ângulos alternos internos:
m ∠3 = m ∠5; m ∠4 = m ∠6
02. Ângulos alternos externos:
m ∠1 = m ∠7; m ∠2 = m
∠8
03. Ângulos conjugados internos:
m ∠3+m ∠6=m ∠4+m ∠5=180°
04. Ângulos conjugados externos:
m ∠1+m ∠8=m ∠2+m ∠7=180°
05. Ângulos correspondentes:
m ∠1 = m ∠5; m ∠4 = m ∠8
m ∠2 = m ∠6; m ∠3 = m ∠7
ÂNGULOS ENTRE DUAS RETAS PARALELAS
E UMA RETA SECANTE
1 2
34
5 6
78

8. α + β + θ = x + yα + β + θ = x + y
α
β
θ
x
y
01- Ângulos que se formam por uma linha poligonal entre
duas retas paralelas.
PROPRIEDADES DOS ÂNGULOS

9. α
β
θ
δ
ε
α + β + θ + δ + ε = 180°α + β + θ + δ + ε = 180°
02- ÂNGULOS ENTRE DUAS RETAS PARALELAS

10. α + β = 180°α + β = 180°
α β
03- ÂNGULOS DE LADOS PERPENDICULARES

12. O complemento da diferença entre o suplemento e o
complemento de um ângulo “X” é igual ao dobro
do complemento do ângulo “X”. Calcule a medida do
ângulo “X”.
90 - { ( ) - ( ) } = ( )180° - X 90° - X 90° - X2
90° - { 180° - X - 90° + X } = 180° - 2X
90° - 90° = 180° - 2X
2X = 180° X = 90°X = 90°
RESOLUÇÃO
Problema Nº 01
A estrutura segundo o enunciado:
Desenvolvendo se obtem:
Logo se reduz a:

13. A soma das medidas dos ângulos é 80° e o
complemento do primeiro ângulo é o dobro da
medida do segundo ângulo. Calcule a diferença
das medidas desses ângulos.
Sejam os ângulos: α e β
α + β = 80°Dado: β = 80° - α ( 1 )
( 90° - α ) = 2β ( 2 )
Substituindo (1) em (2):
( 90° - α ) = 2 ( 80° - α )
90° - α = 160° -2α
β = 10°
α = 70°
α - β = 70°-10°
= 60°
Problema Nº 02
RESOLUÇÃO
Dado:
Diferença das medidas
Resolvendo

14. A soma de seus complementos dos ângulos é 130°
e a diferença de seus suplementos dos mesmos
ângulos é 10°. Calcule a medida destes ângulos.
Sejam os ângulos: α e β
( 90° - α ) ( 90° - β ) = 130°+
β + α = 50° ( 1 )
( 180° - α ) ( 180° - β ) = 10°-
β - α = 10° ( 2 )
Resolvendo: (1) e (2)
β + α = 50°
β - α = 10°
(+)
2β = 60°
β = 30°
α = 20°
Problema Nº 03
RESOLUÇÃO
Do enunciado:
Do enunciado:

15. Se têm ângulos adjacentes AOB e BOC
(AOB<BOC), se traça a bissetriz OM dol ângulo
AOC; se os ângulos BOC e BOM medem 60° e 20°
respectivamente. Calcule a medida do ângulo AOB.
A B
O
C
M
α
α
60°
20°X
Da figura:
α = 60° - 20°
Logo:
X = 40° - 20°
α = 40°
X = 20°X = 20°
Problema Nº 04
RESOLUÇÃO

16. A diferença das medidas dos ângulos adjacentes
AOB e BOC é 30°. Calcule a medida do ângulo
formado pela bissetriz do ângulo AOC com o lado
OB.
A
O
B
C
θ
θ
X
(θ- X)
( θ + X) (θ - X)= 30º
2X=30º
X = 15°X = 15°
Problema Nº 05
RESOLUÇÃO
M
Construção do gráfico segundo o
enunciado
Do enunciado:
AOB - OBC = 30°
-
Logo se substitui pelo que
se observa no gráfico

17. Se têm os ângulos consecutivos AOB, BOC e COD
tal que a m∠AOC = m∠BOD = 90°. Calcule a
medida do ângulo formado pelas bissetrizes dos
ângulos AOB e COD.
A
C
B
D
M
N
αα
β
β
θ
X
Da figura:
2α + θ = 90°
θ + 2β = 90°
( + )
2α + 2θ + 2β = 180°
α + θ + β = 90°
X = α + θ + βX = α + θ + β
X = 90°X = 90°
Problema Nº 06
RESOLUÇÃO
Construção do gráfico segundo o enunciado

18. Se m // n . Calcule a medida do ângulo “X”
80°
30°
α
α
θ
θ
X
m
n
Problema Nº 07

19. 2α + 2θ = 80° + 30°
Pela propriedade
Propriedade do quadrilátero
côncavo
α + θ = 55° (1)
80° = α + θ + X (2)
Substituindo (1) em (2)
80° = 55° + X
X = 25°X = 25°
80°
30°
α
α
θ
θ
X
m
n
RESOLUÇÃO

20. Se m // n . Calcular a medida do ângulo “X”
5α
4α 65°
X
m
n
Problema Nº 08

21. 5α
4α 65°
X
m
n
Pela propiedad:
4α + 5α = 90°
α = 10°α = 10°
Ângulo exterior do triângulo
40° 65°
X = 40° + 65°
X = 105°X = 105°
RESOLUÇÃO

22. Se m // n . Calcule a medida do ângulo ”X”
α
2α
x
m
n
θ
2θ
Problema Nº 09

23. 3α + 3θ = 180°
α + θ = 60°α + θ = 60°
Ângulos entre línhas poligonais
X = α + θ X = 60°X = 60°
RESOLUÇÃO
α
2α
x
m
n
θ
2θ
x
Ângulos conjugados
internos

25. PROBLEMA 01- Se L1 // L2 . Calcule a m ∠ x
A) 10° B) 20° C) 30° D) 40° E) 50°
x
α
α
β
β
4x
3x
L1
L2

26. m
n
30°
X
PROBLEMA 02- Se m // n. Calcule a m ∠ x
A) 18° B) 20° C) 30° D) 36° E) 48°

27. PROBLEMA 03- Se m // n. Calcule a m ∠ α
A) 15° B) 22° C) 27° D) 38° E) 45°
3α
3α
3α
α
m
n

28. PROBLEMA 04- Se m // n. Calcule o valor de “x”
A) 10° B) 15° C) 20° D) 25° E) 30°
40°
95°
α
α
2x
m
n

29. PROBLEMA 05- Calcule m ∠ x
A) 99° B) 100° C) 105° D) 110° E) 120°
3α
6α
x

30. α
4θ
4α
θ
X
m
n
PROBLEMA 06- Se m // n. Calcule m ∠ x
A) 22° B) 28° C) 30° D) 36° E) 60°

31. A) 24° B) 25° C) 32° D) 35° E) 45°
PROBLEMA 07- Se. Calcule m ∠ x
88°
24°
x
α
α
θ
θ
m
n

32. PROBLEMA 08- Se m // n. Calcule m ∠ x
20°
30°
X
m
n
A) 50° B) 60° C) 70° D) 80° E) 30°

33. PROBLEMA 09- Se m//n e θ - α = 80°. Calcule m∠x
A) 60° B) 65° C) 70° D) 75° E) 80°
θ
θ
x
α
α
m
n

34. PROBLEMA 10- Se m // n. Calcule m ∠ x
A) 20° B) 30° C) 40° D) 50° E) 60°
x
x
x
m
n

35. PROBLEMA 11- Se m // n. Calcule m ∠ α
A) 46° B) 48° C) 50° D) 55° E) 60°
180°-2α
α
2α
m
n

36. PROBLEMA 12- Se m // n. Calcule m ∠ x
A) 30° B) 36° C) 40° D) 45° E) 50°
α
α
θ
θ
x
80°
m
n

37. PROBLEMA 13- Se m // n. Calcule m ∠ x
A) 30° B) 40° C) 50° D) 60° E) 70°
80°
α
α
β
β
m
n
x

38. REPOSTAS DOS PROBLEMAS PROPOSTOS
1. 20º 8. 50º
2. 30º 9. 80º
3. 45º 10. 30º
4. 10º 11. 60º
5. 120º 12. 40º
6. 36º 13. 50º
7. 32º