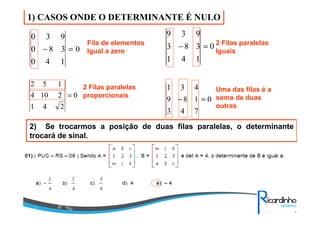
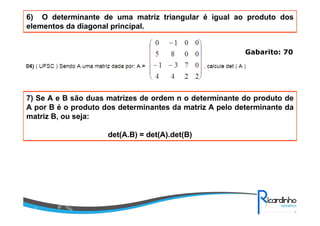
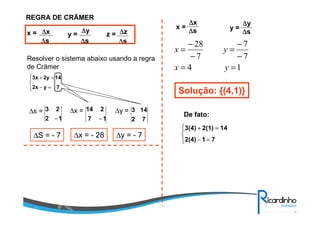
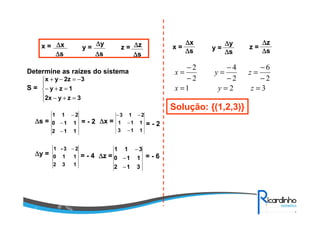
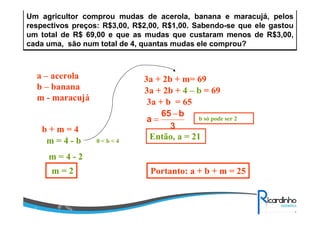
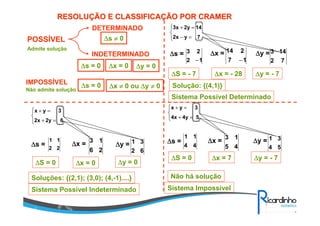
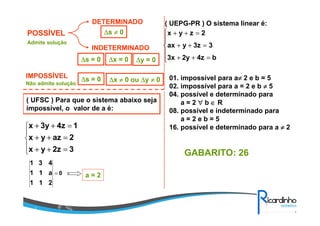
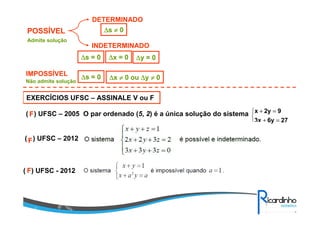
O documento discute sobre matrizes, apresentando:
1) O conceito de matrizes e sua notação;
2) Exemplos de construção de matrizes;
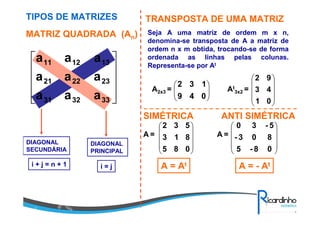
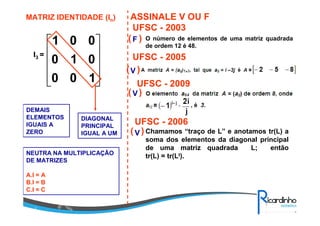
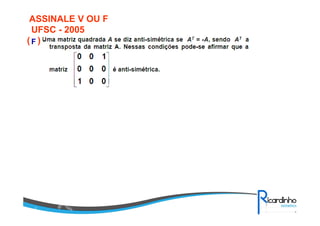
3) Tipos de matrizes como quadrada, diagonal, simétrica etc;
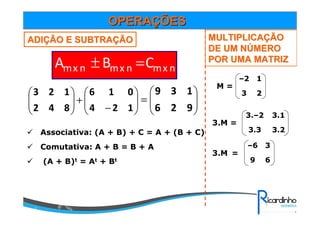
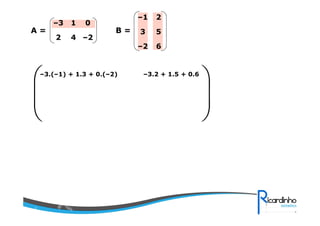
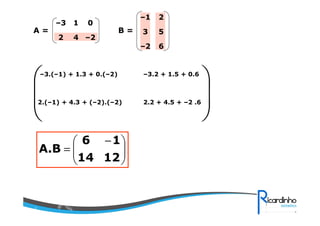
4) Operações com matrizes como soma, subtração, multiplicação e transposta.

![Uma matriz do tipo m x n, é uma tabela formada por m.n
elementos dispostos em m linhas e n colunas. As matrizes
são representadas através de parênteses ( ), colchetes [ ] ou
através de barras duplas || ||
EXEMPLOS
−
−
=
12
36
28
13
02
A
−
−
=
313
524
B
5x2
2x3
A = (aij) mxn](https://image.slidesharecdn.com/matrizes-determinantes-sistemaslineares-140317092721-phpapp02/85/Matrizes-determinantes-sistemaslineares-2-320.jpg)