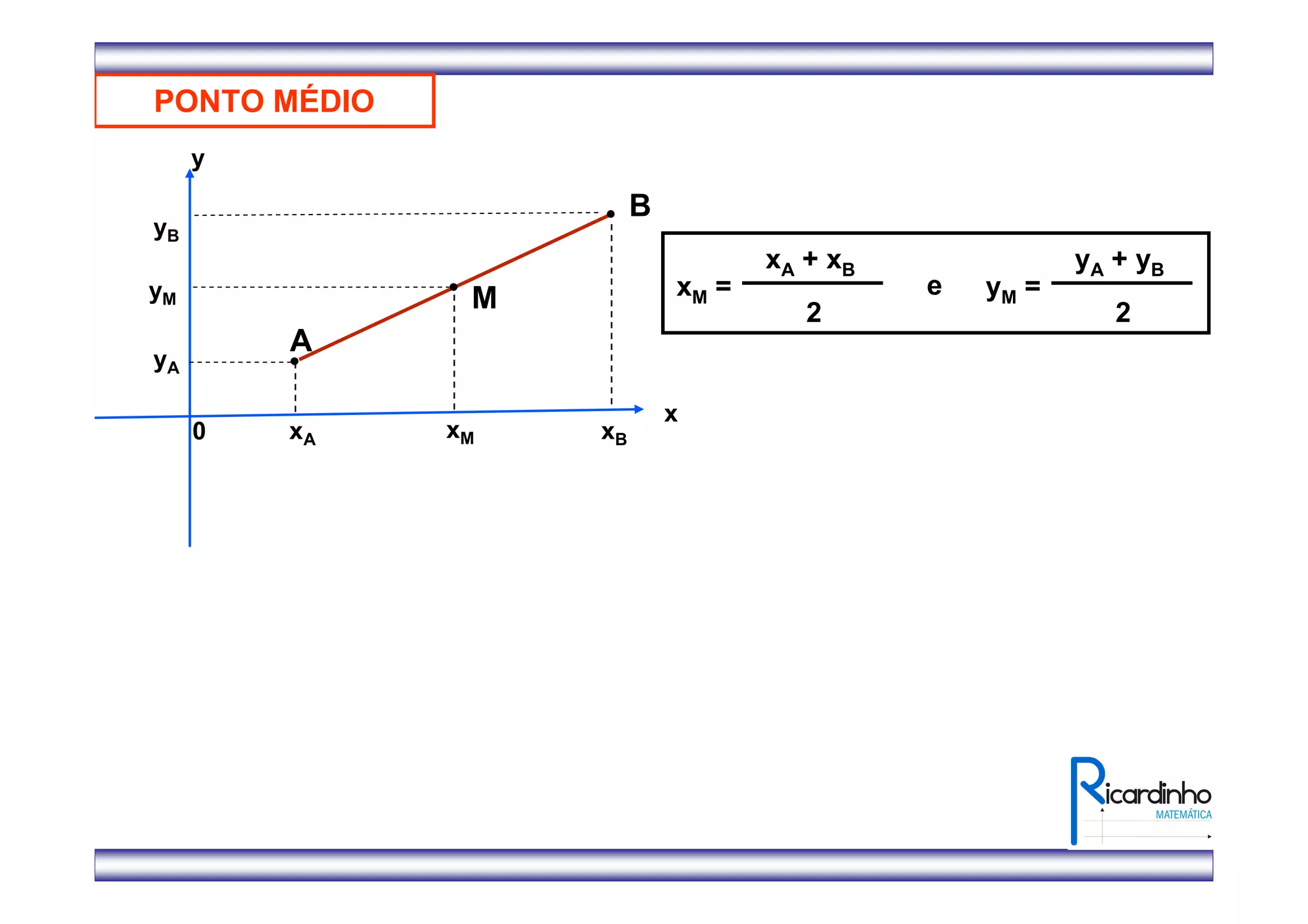
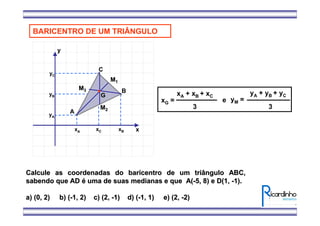
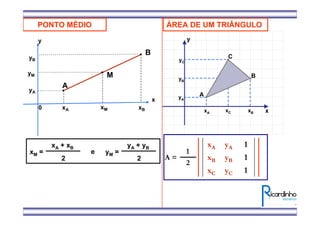
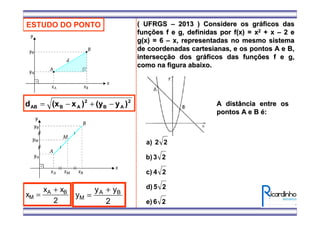
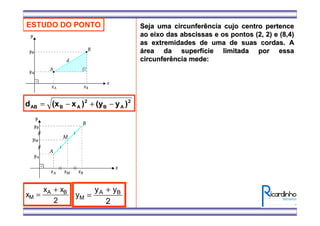
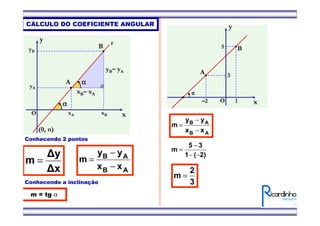
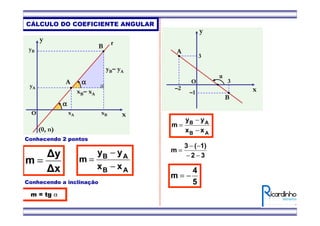
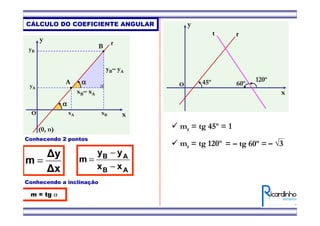
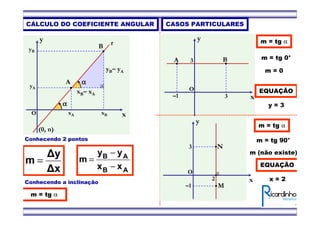
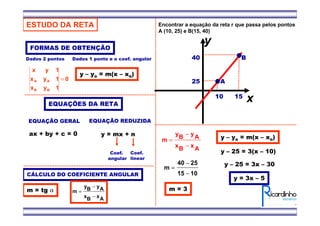
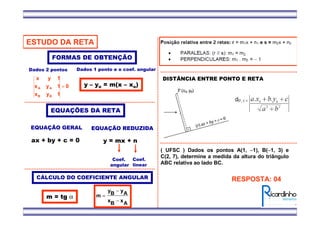
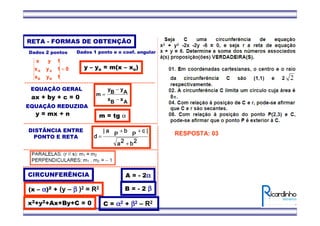
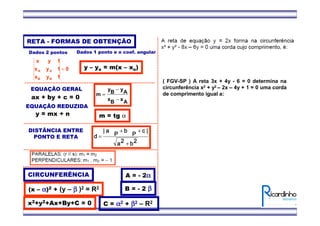
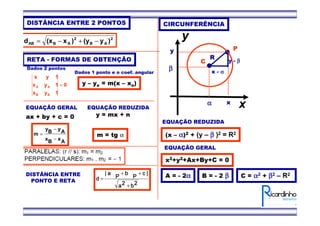
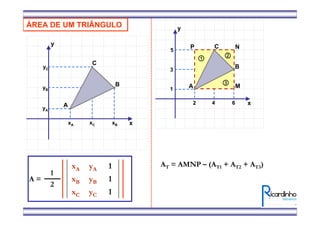
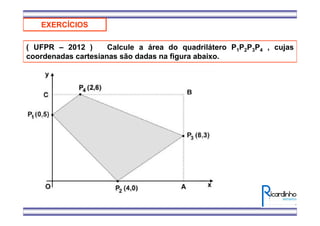
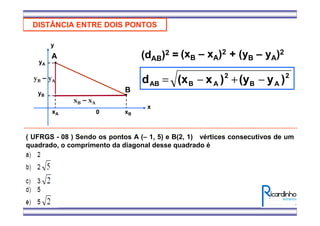
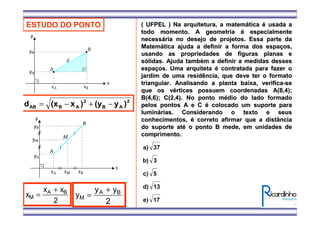
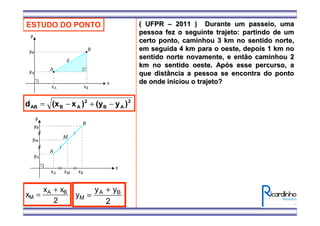
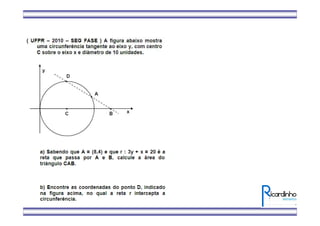
1) O documento apresenta fórmulas para calcular o ponto médio e o baricentro de triângulos a partir das coordenadas de seus vértices. 2) Também mostra como calcular a área de um triângulo a partir das coordenadas de seus vértices. 3) Há um exemplo de exercício que pede para calcular as coordenadas do baricentro de um triângulo ABC, sabendo que AD é uma mediana e as coordenadas de A e D.

1. B
A
M
xBxMxA
yB
yM
yA
x
y
xM =
xA + xB
2
yM =
yA + yB
2
e
0
PONTO MÉDIO

2. x
y
xC
yA
A
B
C
xA xB
yB
yC
BARICENTRO DE UM TRIÂNGULO
MM11
MM22
MM33
GG
xG =
xA + xB + xC
3
yM =
yA + yB + yC
3
e
Calcule as coordenadas do baricentro de um triângulo ABC,Calcule as coordenadas do baricentro de um triângulo ABC,
sabendo que ADsabendo que AD éé uma de suas medianas e que A(uma de suas medianas e que A(--5, 8) e D(1,5, 8) e D(1, --1).1).
a) (0, 2) b) (a) (0, 2) b) (--1, 2) c) (2,1, 2) c) (2, --1) d) (1) d) (--1, 1) e) (2,1, 1) e) (2, --2)2)

3. x
y
xC
yA
A
B
C
xA xB
yB
yC
ÁREA DE UM TRIÂNGULO
1yCxC
1yBxB
1yAxA
A =
1
2
x
y
4
1 A
B
C
2 6
3
5
③③③③
①①①① ②②②②
M
NP
AT = AMNP – (AT1 + AT2 + AT3)

4. EXERCÍCIOS
( UFPR – 2012 ) Calcule a área do quadrilátero P1P2P3P4 , cujas
coordenadas cartesianas são dadas na figura abaixo.

5. ( FURG-RS ) Os pontos (1,3), (2,7) e (4,k) do plano cartesiano estão alinhados se e
somente se:
a) k = 15
b) k = 11
c) k = 14
d) k = 12
e) k = 13

6. B
A
M
xBxMxA
yB
yM
yA
x
y
xM =
xA + xB
2
yM =
yA + yB
2
e
0
PONTO MÉDIO
x
y
xC
yA
A
B
C
xA xB
yB
yC
ÁREA DE UM TRIÂNGULO
1yCxC
1yBxB
1yAxA
A =
1
2

7. DISTÂNCIA ENTRE DOIS PONTOS
A
B
xA xB
yA
yB
x
y
0
(dAB)2 = (xB – xA)2
xB – xA
yB – yA
+ (yB – yA)2
2
AB
2
ABAB )y(y)x(xd −+−=
( UFRGS - 08 ) Sendo os pontos A (– 1, 5) e B(2, 1) vértices consecutivos de um
quadrado, o comprimento da diagonal desse quadrado é

8. ESTUDO DO PONTO
2
AB
2
ABAB )y(y)x(xd −+−=
x
x x
M
A B
=
+
2
y
y y
M
A B
=
+
2
( UFPEL ) Na arquitetura, a matem( UFPEL ) Na arquitetura, a matemááticatica éé usada ausada a
todo momento. A geometriatodo momento. A geometria éé especialmenteespecialmente
necessnecessáária no desejo de projetos. Essa parte daria no desejo de projetos. Essa parte da
MatemMatemáática ajuda a definir a forma dos espatica ajuda a definir a forma dos espaçços,os,
usando as propriedades de figuras planas eusando as propriedades de figuras planas e
ssóólidas. Ajuda tamblidas. Ajuda tambéém a definir a medidas dessesm a definir a medidas desses
espaespaçços. Uma arquitetaos. Uma arquiteta éé contratada para fazer ocontratada para fazer o
jardim de uma residência, que deve ter o formatojardim de uma residência, que deve ter o formato
triangular. Analisando a planta baixa, verificatriangular. Analisando a planta baixa, verifica--sese
que os vque os véértices possuem coordenadasrtices possuem coordenadas A(8,4);A(8,4);
B(4,6); C(2,4). No ponto mB(4,6); C(2,4). No ponto méédio do lado formadodio do lado formado
pelos pontos A e Cpelos pontos A e C éé colocado um suporte paracolocado um suporte para
luminlumináárias. Considerando o texto e seusrias. Considerando o texto e seus
conhecimentos,conhecimentos, éé correto afirmar que a distânciacorreto afirmar que a distância
do suporte atdo suporte atéé o ponto B mede, em unidades deo ponto B mede, em unidades de
comprimento.comprimento.
17e)
13d)
5c)
3b)
37a)

9. ESTUDO DO PONTO
2
AB
2
ABAB )y(y)x(xd −+−=
x
x x
M
A B
=
+
2
y
y y
M
A B
=
+
2
( UFPR( UFPR –– 2011 ) Durante um passeio, uma2011 ) Durante um passeio, uma
pessoa fez o seguinte trajeto: partindo de umpessoa fez o seguinte trajeto: partindo de um
certo ponto, caminhou 3 km no sentido norte,certo ponto, caminhou 3 km no sentido norte,
em seguida 4 km para o oeste, depois 1 km noem seguida 4 km para o oeste, depois 1 km no
sentido norte novamente, e então caminhou 2sentido norte novamente, e então caminhou 2
km no sentido oeste. Apkm no sentido oeste. Apóós esse percurso, as esse percurso, a
que distância a pessoa se encontra do pontoque distância a pessoa se encontra do ponto
de onde iniciou o trajeto?de onde iniciou o trajeto?

10. ESTUDO DO PONTO
2
AB
2
ABAB )y(y)x(xd −+−=
x
x x
M
A B
=
+
2
y
y y
M
A B
=
+
2
( UFRGS( UFRGS –– 2013 ) Considere os gr2013 ) Considere os grááficos dasficos das
funfunçções f e g, definidas por f(x) = xões f e g, definidas por f(x) = x22 + x+ x –– 2 e2 e
g(x) = 6g(x) = 6 –– x, representadas no mesmo sistemax, representadas no mesmo sistema
de coordenadas cartesianas, e os pontos A e B,de coordenadas cartesianas, e os pontos A e B,
intersecintersecçção dos grão dos grááficos das funficos das funçções f e g,ões f e g,
como na figura abaixo.como na figura abaixo.
A distância entre osA distância entre os
pontos A e Bpontos A e B éé::
26e)
25d)
24c)
23b)
22a)

11. ESTUDO DO PONTO
2
AB
2
ABAB )y(y)x(xd −+−=
x
x x
M
A B
=
+
2
y
y y
M
A B
=
+
2
Seja uma circunferência cujo centro pertenceSeja uma circunferência cujo centro pertence
ao eixo das abscissas e os pontos (2, 2) e (8,4)ao eixo das abscissas e os pontos (2, 2) e (8,4)
as extremidades de uma de suas cordas. Aas extremidades de uma de suas cordas. A
áárea da superfrea da superfíície limitada por essacie limitada por essa
circunferência mede:circunferência mede:

12. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
x
y
O 3
1
r
2
3
A
B
P(x, y)
133
121
1yx
= 0
x + 3y + 6 – 3 – 3x – 2y = 0
– 2x + y + 3 = 0 geral
y = 2x – 3 reduzida
Coef.
angular
Coef.
linear

13. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
( UDESC ) A soma do coeficiente angular( UDESC ) A soma do coeficiente angular
com o coeficiente linear da reta quecom o coeficiente linear da reta que
passa pelos pontospassa pelos pontos A(A(1,5) e1,5) e B(B( 4,14)4,14) éé::

14. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
CÁLCULO DO COEFICIENTE ANGULAR
B
x
y
O
yB
yA
xBxA
A
αααα
(0, n)
αααα
yB– yA
xB– xA
r
AB
AB
xx
yy
m
−
−
=
m = tg α
∆x
∆y
m =
Conhecendo 2 pontos
Conhecendo a inclinação

15. CÁLCULO DO COEFICIENTE ANGULAR
B
x
y
O
yB
yA
xBxA
A
αααα
(0, n)
αααα
yB– yA
xB– xA
r
AB
AB
xx
yy
m
−
−
=
m = tg α
∆x
∆y
m =
Conhecendo 2 pontos
Conhecendo a inclinação
x
y
O
α
A
B
–2 1
3
5
2)(1
35
m
−−
−
=
AB
AB
xx
yy
m
−
−
=
3
2
m =

16. CÁLCULO DO COEFICIENTE ANGULAR
B
x
y
O
yB
yA
xBxA
A
αααα
(0, n)
αααα
yB– yA
xB– xA
r
AB
AB
xx
yy
m
−
−
=
m = tg α
∆x
∆y
m =
Conhecendo 2 pontos
Conhecendo a inclinação
x
y
O
α
A
B
–2
3
3
–1
32
1)(3
m
−−
−−
=
AB
AB
xx
yy
m
−
−
=
5
4
m −=

17. CÁLCULO DO COEFICIENTE ANGULAR
B
x
y
O
yB
yA
xBxA
A
αααα
(0, n)
αααα
yB– yA
xB– xA
r
AB
AB
xx
yy
m
−
−
=
m = tg α
∆x
∆y
m =
Conhecendo 2 pontos
Conhecendo a inclinação
x
y
O
120º45º
rt
mr = tg 45º = 1
mt = tg 120º – √3= – tg 60º =
60º

18. CÁLCULO DO COEFICIENTE ANGULAR
B
x
y
O
yB
yA
xBxA
A
αααα
(0, n)
αααα
yB– yA
xB– xA
r
AB
AB
xx
yy
m
−
−
=
m = tg α
∆x
∆y
m =
Conhecendo 2 pontos
Conhecendo a inclinação
CASOS PARTICULARES
x
y
O
A B
–1 3
3
m = tg α
m = tg 0°
m = 0
EQUAÇÃO
y = 3
x
y
O
M
N
–1
2
3
m = tg α
m = tg 90°
m (não existe)
EQUAÇÃO
x = 2

19. ( UFRGS( UFRGS –– 2012 ) As equa2012 ) As equaçções das retas representadas no sistema deões das retas representadas no sistema de
coordenadas cartesianas abaixo são:coordenadas cartesianas abaixo são:
2x + y2x + y –– 3 = 0, 5x3 = 0, 5x –– 4y4y –– 8 = 0 e x8 = 0 e x –– 3y + 3 = 0.3y + 3 = 0.
As equaAs equaçções deões de rr ee ss são, respectivamente,são, respectivamente,
a) 2x + ya) 2x + y –– 3 = 0 e x3 = 0 e x –– 3y + 3 = 0.3y + 3 = 0.
b) 2x + yb) 2x + y –– 3 = 0 e 5x3 = 0 e 5x –– 4y4y –– 8 = 0.8 = 0.
c) 5xc) 5x –– 4y4y –– 8 = 0 e x8 = 0 e x –– 3y + 3 = 0.3y + 3 = 0.
d) xd) x –– 3y + 3 = 0 e 2x + y3y + 3 = 0 e 2x + y –– 3 = 0.3 = 0.
e) xe) x –– 3y + 3 = 0 e 5x3y + 3 = 0 e 5x –– 4y4y –– 8 = 0.8 = 0.

20. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
CÁLCULO DO COEFICIENTE ANGULAR
AxBx
AyBy
m
−
−
=m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
Encontrar a equação da reta r que passa pelos pontos
A (10, 25) e B(15, 40)
AxBx
AyBy
m
−
−
=
1015
2540
m
−
−
=
m = 3
y – yo = m(x – xo)
y – 25 = 3(x – 10)
y – 25 = 3x – 30
y = 3x – 5
x
y
B
15
40
10
25 A

21. ( UFPR ) Sabe-se que a reta r passa pelos pontos A = (−2,0) e P = (0,1) e que a
reta s é paralela ao eixo das ordenadas e passa pelo ponto Q = (4,2). Se B é o
ponto em que a reta s intercepta o eixo das abscissas e C é o ponto de
interseção das retas r e s, então o perímetro do triângulo ABC é:
)3(5e)
)33(3d)
)5(3c)
)33(5b)
)53(3a)
+
+
+
+
+
5
5

22. ( UFSC ) Calcular a área da região limitada pelas retas y = 5, 5x + 2y - 95 = 0, x = 0
e y = 0.
GABARITO: 90

23. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
CÁLCULO DO COEFICIENTE ANGULAR
AxBx
AyBy
m
−
−
=m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
( UFRGS ) Os pontos A(-1,3) e B(5,-1) são
extremidades de uma das diagonais de um
quadrado. A equação da reta suporte da outra
diagonal é:
a) 2x - 3y - 1 = 0
b) 2x + 3y - 7 = 0
c) 3x + 2y - 8 = 0
d) 3x - 2y - 4 = 0

24. ( UFPR – 2011 ) Um balão de ar quente foi lançado de uma rampa inclinada.
Utilizando o plano cartesiano, a figura ao lado descreve a situação de maneira
simplificada. Ao ser lançado, o balão esticou uma corda presa aos pontos P e Q,
mantendo-se fixo no ar. As coordenadas do ponto P, indicado na figura, são,
então:
a) (21,7).
b) (22,8).
c) (24,12).
d) (25,13).
e) (26,15).

25. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
CÁLCULO DO COEFICIENTE ANGULAR
AxBx
AyBy
m
−
−
=m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
DISTÂNCIA ENTRE PONTO E RETA
( UFSC – 2010 ) Em um mapa de um deserto,
localizado sobre um sistema de eixos cartesianos
ortogonal, o faminto Coiote, cuja posição é dada
pelo ponto P(1,2), vai tentar capturar o Papa-léguas,
que se aproxima do Coiote descrevendo uma
trajetória retilínea segundo a equação 3x + 4y = 31. A
menor distância que o Coiote deve percorrer para
capturar o Papa-léguas é de:
RESPOSTA: 04

26. ESTUDO DA RETA
EQUAÇÕES DA RETA
EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
Coef.
angular
Coef.
linear
FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
CÁLCULO DO COEFICIENTE ANGULAR
AxBx
AyBy
m
−
−
=m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
DISTÂNCIA ENTRE PONTO E RETA
( UFSC ) Dados os pontos A(1, −−−−1), B(−−−−1, 3) e
C(2, 7), determine a medida da altura do triângulo
ABC relativa ao lado BC.
RESPOSTA: 04

27. ESTUDO DA CIRCUNFERÊNCIA
x
y
C
αααα x
y P
ββββ x - αααα
y - ββββ
R
EQUAÇÃO DA CIRCUNFERÊNCIA
EQUAÇÃO REDUZIDA
(x – αααα)2 + (y – ββββ )2 = R2
EQUAÇÃO GERAL
x2 + y2 + Ax + By + C = 0
A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2
Determine as coordenadas do centro e o raio das circunferências:
a) x2 + y2 – 4x – 6y - 12 = 0
b) x2 + y2 – 8x – 2y + 1 = 0
a) C (2, 3); R = 5
b) C (4, 1); R = 4

28. EQUAÇÃO DA CIRCUNFERÊNCIA
EQUAÇÃO REDUZIDA
(x – αααα)2 + (y – ββββ )2 = R2
EQUAÇÃO GERAL
x2 + y2 + Ax + By + C = 0
A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2
Resposta: 12

29. EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
RETA - FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
AxBx
AyBy
m
−
−
=
m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
2222bbbb2222aaaa
||||cccc
PPPP
b
.
y
b
.
y
b
.
y
b
.
y
PPPP
a
.
x
a
.
x
a
.
x
a
.
x
||||
dddd
+
++
=
DISTÂNCIA ENTRE
PONTO E RETA
CIRCUNFERÊNCIA
(x – αααα)2 + (y – ββββ )2 = R2
x2+y2+Ax+By+C = 0
A = - 2αααα
B = - 2 ββββ
C = αααα2 + ββββ2 – R2
RESPOSTA: 03

30. EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
RETA - FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
AxBx
AyBy
m
−
−
=
m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
2222bbbb2222aaaa
||||cccc
PPPP
b
.
y
b
.
y
b
.
y
b
.
y
PPPP
a
.
x
a
.
x
a
.
x
a
.
x
||||
dddd
+
++
=
DISTÂNCIA ENTRE
PONTO E RETA
CIRCUNFERÊNCIA
(x – αααα)2 + (y – ββββ )2 = R2
x2+y2+Ax+By+C = 0
A = - 2αααα
B = - 2 ββββ
C = αααα2 + ββββ2 – R2
RESPOSTA: 18

31. EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
RETA - FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
AxBx
AyBy
m
−
−
=
m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
2222bbbb2222aaaa
||||cccc
PPPP
b
.
y
b
.
y
b
.
y
b
.
y
PPPP
a
.
x
a
.
x
a
.
x
a
.
x
||||
dddd
+
++
=
DISTÂNCIA ENTRE
PONTO E RETA
CIRCUNFERÊNCIA
(x – αααα)2 + (y – ββββ )2 = R2
x2+y2+Ax+By+C = 0
A = - 2αααα
B = - 2 ββββ
C = αααα2 + ββββ2 – R2
( FGV-SP ) A reta 3x + 4y - 6 = 0 determina na
circunferência x2 + y2 – 2x – 4y + 1 = 0 uma corda
de comprimento igual a:

37. EQUAÇÃO GERAL
ax + by + c = 0
EQUAÇÃO REDUZIDA
y = mx + n
RETA - FORMAS DE OBTENÇÃO
0
1yx
1yx
1yx
BB
AA =
Dados 2 pontos
AxBx
AyBy
m
−
−
= m = tg α
Dados 1 ponto e o coef. angular
y – yo = m(x – xo)
2222bbbb2222aaaa
||||cccc
PPPP
b
.
y
b
.
y
b
.
y
b
.
y
PPPP
a
.
x
a
.
x
a
.
x
a
.
x
||||
dddd
+
++
=
DISTÂNCIA ENTRE
PONTO E RETA
CIRCUNFERÊNCIA
(x – αααα)2 + (y – ββββ )2 = R2
x2+y2+Ax+By+C = 0
A = - 2αααα B = - 2 ββββ C = αααα2 + ββββ2 – R2
2
AB
2
ABAB )y(y)x(xd −+−=
x
y
C
αααα x
y P
ββββ x - αααα
y - ββββ
R
DISTÂNCIA ENTRE 2 PONTOS
EQUAÇÃO REDUZIDA
EQUAÇÃO GERAL

38. POSIÇÕES RELATIVAS ENTRE DUAS CIRCUNFERÊNCIAS ( R > r)
TANGENTES
C1 C2
C1 C2
R rR
d(C1, C2) = R + r
r
d(C1, C2) = R – r
SECANTES
C1 C2
R
R – r < d(C1, C2) < R + r
r
NÃO SE INTERCEPTAM
C1
C2
d(C1, C2) > R + r
C1
C2
d(C1, C2) < R – r