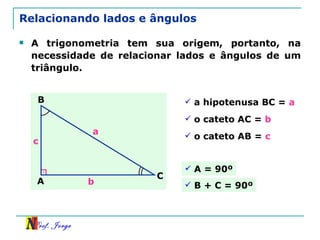
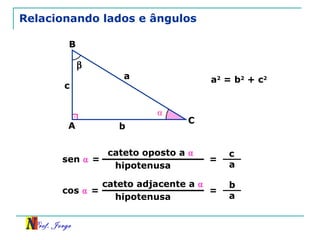
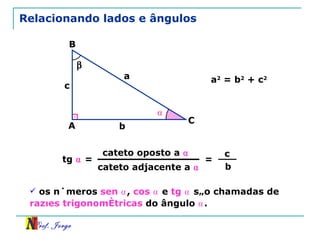
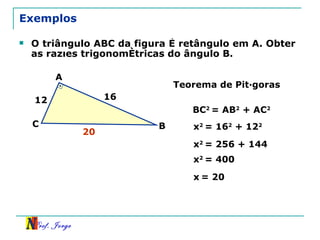
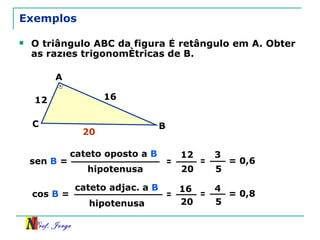
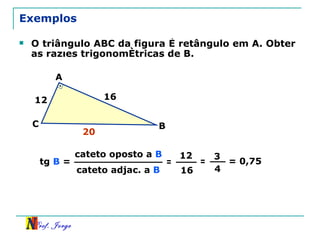
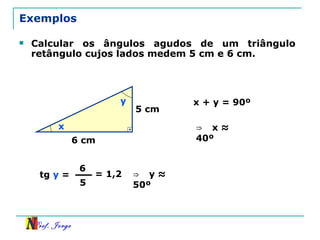
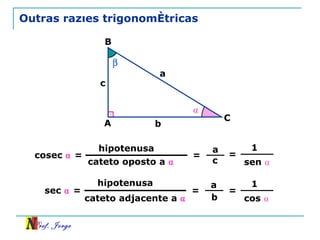
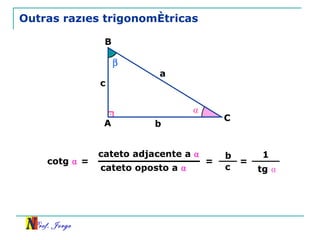
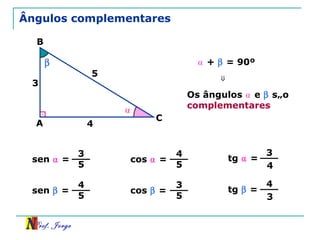
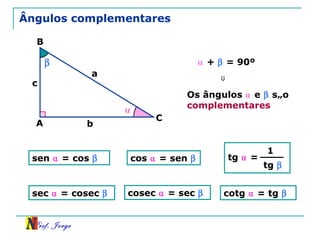
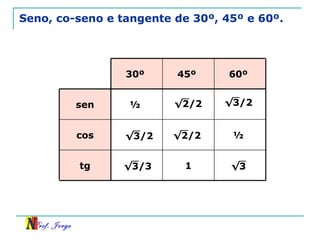
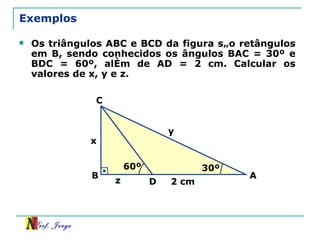
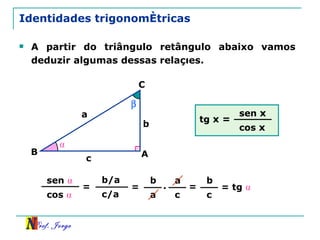
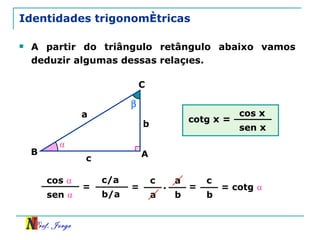
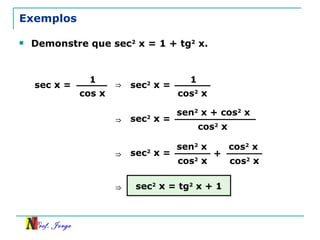
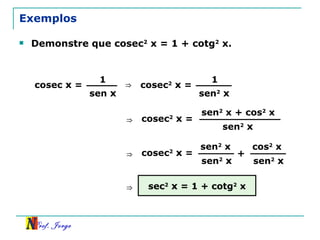
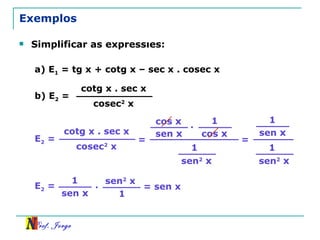
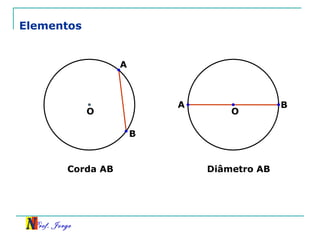
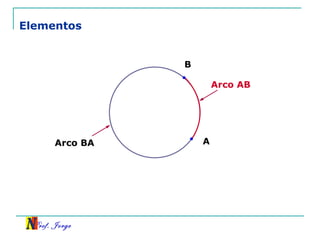
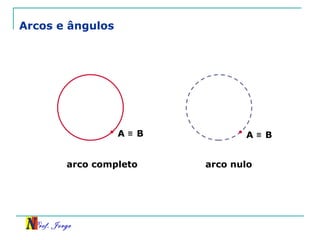
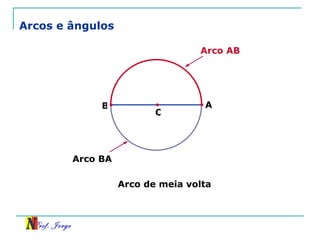
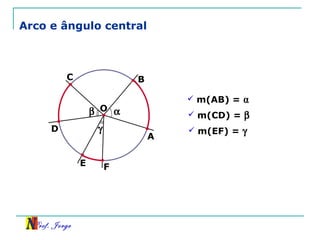
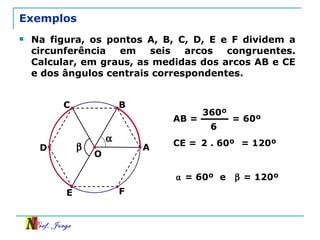
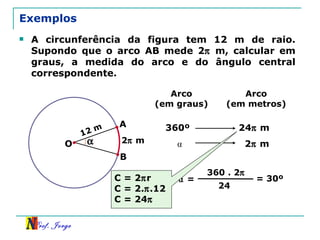
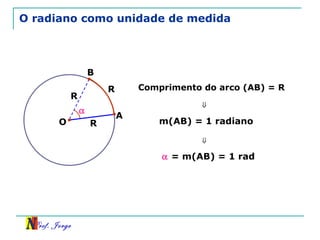
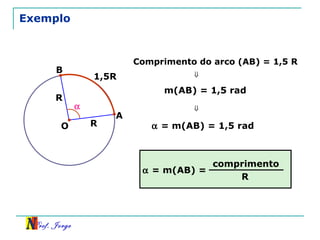
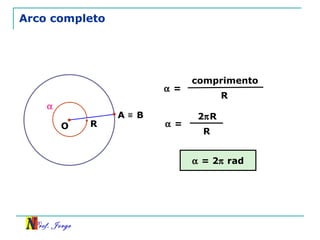
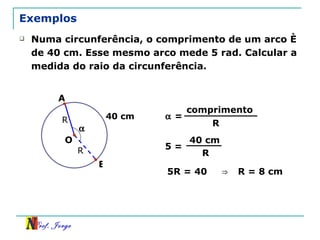
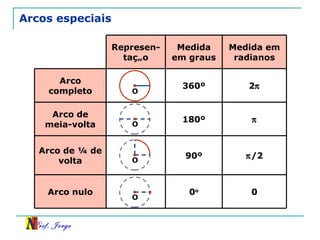
O documento discute trigonometria em triângulos retângulos, relacionando lados e ângulos. Apresenta as definições de seno, cosseno e tangente de um ângulo em termos dos catetos e hipotenusa. Fornece exemplos de cálculo destas razões trigonométricas e introduz outras identidades trigonométricas.

1. Trigonometria no Triângulo Retângulo

2. Relacionando lados e ângulos A trigonometria tem sua origem, portanto, na necessidade de relacionar lados e ângulos de um triângulo. a hipotenusa BC = a A B C a b c o cateto AC = b o cateto AB = c A = 90º B + C = 90º

3. Relacionando lados e ângulos A B C a b c a 2 = b 2 + c 2 ⍺ cateto oposto a ⍺ hipotenusa = sen ⍺ = c a cateto adjacente a ⍺ hipotenusa = cos ⍺ = b a 

4. Relacionando lados e ângulos A B C a b c a 2 = b 2 + c 2 ⍺ cateto oposto a ⍺ = tg ⍺ = c b cateto adjacente a ⍺  os números sen ⍺ , cos ⍺ e tg ⍺ são chamadas de razões trigonométricas do ângulo ⍺ .

5. Exemplos O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas do ângulo B. 12 16 A B C Teorema de Pitágoras BC 2 = AB 2 + AC 2 x 2 = 16 2 + 12 2 x 2 = 256 + 144 x 2 = 400 x = 20 20

6. Exemplos O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B. cateto oposto a B hipotenusa sen B = = 12 20 = 3 5 = 0,6 cateto adjac. a B hipotenusa cos B = = 16 20 = 4 5 = 0,8 12 16 A B C 20

7. Exemplos O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B. cateto oposto a B cateto adjac. a B tg B = = 12 16 = 3 4 = 0,75 12 16 A B C 20

8. Exemplos Calcular os ângulos agudos de um triângulo retângulo cujos lados medem 5 cm e 6 cm. 5 cm 16 6 cm x y tg y = 6 5 = 1,2 ⇒ y ≈ 50º x + y = 90º ⇒ x ≈ 40º

9. Outras razões trigonométricas

10. Outras razões trigonométricas  A B C a b c ⍺ cateto oposto a ⍺ hipotenusa = cosec ⍺ = a c cateto adjacente a ⍺ hipotenusa = sec ⍺ = a b = 1 sen ⍺ = 1 cos ⍺

11. Outras razões trigonométricas  A B C a b c ⍺ cateto oposto a ⍺ = cotg ⍺ = b c cateto adjacente a ⍺ = 1 tg ⍺

12. Seno, co-seno e tangente de ângulos complementares

13. Ângulos complementares  A B C 5 4 3 ⍺ +  = 90º ⍺ tg ⍺ = 3 4 ⇒ Os ângulos ⍺ e  são complementares sen ⍺ = 3 5 cos ⍺ = 4 5 tg  = 4 3 sen  = 4 5 cos  = 3 5

14. Ângulos complementares  A B C a b c ⍺ +  = 90º ⍺ tg ⍺ = 1 tg  ⇒ Os ângulos ⍺ e  são complementares sen ⍺ = cos  cos ⍺ = sen  sec ⍺ = cosec  cosec ⍺ = sec  cotg ⍺ = tg 

15. Exemplo No triângulo retângulo da figura, temos: 1 cm 2 cm t I. sen t = ½ II. sec t = √ 5 2 III. tg t = 2 A(s) afirmativa(s) verdadeira(s) é(são): a) I b) II c) III d) II e III e) I, II e III

16. Seno, co-seno e tangente de 30º, 45º e 60º.

17. Seno, co-seno e tangente de 30º, 45º e 60º. 1 tg ½ cos ½ sen 60º 45º 30º √ 2/2 √ 2/2 √ 3/2 √ 3/2 √ 3/3 √ 3

18. Exemplos A partir dos dados apresentados na figura, determinar as medidas indicadas por x e y. x 16 y 30º sen 30º = x 12 12 cm ⇒ x = 12 . 1/2 ⇒ x = 6 cm cos 30º = y 12 ⇒ x = 12 . √ 3 /2 ⇒ x = 6 √ 3 cm

19. Exemplos Os triângulos ABC e BCD da figura são retângulos em B, sendo conhecidos os ângulos BAC = 30º e BDC = 60º, além de AD = 2 cm. Calcular os valores de x, y e z. 30º A B C D x y z 2 cm 60º

20. Identidades trigonométricas

21. Identidades trigonométricas Ferramentas de grande aplicabilidade sendo utilizadas para: Obter uma razão trigonométrica, para um dado ângulo, a partir de outra razão cujo valor seja conhecido. Simplificar expressões extensas envolvendo várias relações trigonométricas para um mesmo ângulo.

22. Identidades trigonométricas A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações.  A C B a c b ⍺ b 2 + c 2 = a 2 ( : a 2 ) b 2 a 2 + c 2 a 2 = a 2 a 2 b a + c a = 1 2 2 sen ⍺ + cos ⍺ = 1 2 2 ⇒ sen 2 x + cos 2 x = 1

23. Identidades trigonométricas A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações. b/a c/a  A C B a c b ⍺ sen ⍺ cos ⍺ = = b a . a c = b c = tg ⍺ tg x = sen x cos x

24. Identidades trigonométricas A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações. c/a b/a  A C B a c b ⍺ cos ⍺ sen ⍺ = = c a . a b = c b = cotg ⍺ cotg x = cos x sen x

25. Identidades trigonométricas - Resumo 1) sen 2 x + cos 2 x = 1 Relação fundamental 2) tg x = sen x cos x 3) cotg x = cos x sen x (cos x ≠ 0) (sen x ≠ 0) = 1 tg x 4) sec x = 1 cos x 5) cosec x = 1 sen x (cos x ≠ 0) (sen x ≠ 0)

26. Exemplos Demonstre que sec 2 x = 1 + tg 2 x. sec x = 1 cos x ⇒ sec 2 x = 1 cos 2 x ⇒ sec 2 x = sen 2 x + cos 2 x cos 2 x ⇒ sec 2 x = sen 2 x cos 2 x + cos 2 x cos 2 x ⇒ sec 2 x = tg 2 x + 1

27. Exemplos Demonstre que cosec 2 x = 1 + cotg 2 x. cosec x = 1 sen x ⇒ cosec 2 x = 1 sen 2 x ⇒ cosec 2 x = sen 2 x + cos 2 x sen 2 x ⇒ cosec 2 x = sen 2 x sen 2 x + cos 2 x sen 2 x ⇒ sec 2 x = 1 + cotg 2 x

28. Exemplos Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, co-tangente, secante e a co-secante desse ângulo. sen 2 x + cos 2 x ⇒ 3 5 + 2 cos 2 x = 1 ⇒ 9 25 + cos 2 x = 1 ⇒ 9 25 – cos 2 x = 1 = 25 – 9 25 ⇒ cos x = = 16 25 ± 4/5 ⇒ cos x = 4/5

29. Exemplos Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, co-tangente, secante e a co-secante desse ângulo. tg x = sen x cos x = 3 5 4 5 = 3 4 cotg x = 1 tg x = 1 3 4 = 4 3

30. Exemplos Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, co-tangente, secante e a co-secante desse ângulo. sec x = 1 cos x = 1 4 5 = 5 4 cosec x = 1 sen x = 1 3 5 = 5 3

31. Exemplos Simplificar as expressões: a) E 1 = tg x + cotg x – sec x . cosec x b) E 2 = cotg x . sec x cosec 2 x E 1 = tg x + cotg x – sec x . cosec x E 1 = sen x cos x + cos x sen x – 1 cos x 1 sen x . E 1 = sen 2 x sen x . cos x + cos 2 x – 1 = sen x . cos x 1 – 1 = 0

32. Exemplos Simplificar as expressões: cos x sen x 1 cos x 1 sen 2 x a) E 1 = tg x + cotg x – sec x . cosec x b) E 2 = cotg x . sec x cosec 2 x E 2 = cotg x . sec x cosec 2 x = . = 1 sen x 1 sen 2 x E 2 = 1 sen x . sen 2 x 1 = sen x

33. Ângulos e arcos na circunferência

34. Circunferência O A B C D E P r r r r r r

35. Elementos B A B A O O Corda AB Diâmetro AB

36. Elementos A B Arco AB Arco BA

37. Arcos e ângulos A ≡ B A ≡ B arco completo arco nulo

38. Arcos e ângulos A B Arco de meia volta O Arco AB Arco BA

39. Arco e ângulo central A B O C  D E F   m(AB) = ⍺ m(CD) =  m(EF) = 

40. O grau como unidade de medida 0 o 10 o 20 o 30 o 40 o 50 o 60 o 70 o 80 o 90 o 100 o 110 o 120 o 130 o 140 o 150 o 160 o 170 o 180 o 190 o 200 o 210 o 220 o 230 o 240 o 250 o 260 o 270 o 280 o 290 o 300 o 310 o 320 o 330 o 340 o 350 o

41. O grau como unidade de medida 0 o 10 o 20 o 30 o 40 o 50 o 60 o 70 o 80 o 90 o 100 o 110 o 120 o 130 o 140 o 150 o 160 o 170 o 180 o 190 o 200 o 210 o 220 o 230 o 240 o 250 o 260 o 270 o 280 o 290 o 300 o 310 o 320 o 330 o 340 o 350 o

42. O grau como unidade de medida 0 o 10 o 20 o 30 o 40 o 50 o 60 o 70 o 80 o 90 o 100 o 110 o 120 o 130 o 140 o 150 o 160 o 170 o 180 o 190 o 200 o 210 o 220 o 230 o 240 o 250 o 260 o 270 o 280 o 290 o 300 o 310 o 320 o 330 o 340 o 350 o 1 o 1º = 360 1

43. Exemplos Na figura, os pontos A, B, C, D, E e F dividem a circunferência em seis arcos congruentes. Calcular, em graus, as medidas dos arcos AB e CE e dos ângulos centrais correspondentes. A B O C  D E F  AB = 360º 6 = 60º CE = 2 . 60º = 120º ⍺ = 60º e  = 120º

44. Exemplos A circunferência da figura tem 12 m de raio. Supondo que o arco AB mede 2  m, calcular em graus, a medida do arco e do ângulo central correspondente. A B O  2  m 12 m Arco (em graus) 2  m ⍺ = 360 . 2  24 Arco (em metros) 360º 24  m ⍺ = 30º C = 2  r C = 2.  .12 C = 24 

45. O radiano como unidade de medida A R O R  R B Comprimento do arco (AB) = R ⇓ m(AB) = 1 radiano ⇓  = m(AB) = 1 rad

46. Exemplo A R O R  1,5R B Comprimento do arco (AB) = 1,5 R ⇓ m(AB) = 1,5 rad ⇓  = m(AB) = 1,5 rad  = m(AB) = comprimento R

47. Arco completo  = comprimento R  = 2  R R R A ≡ B O   = 2  rad

48. Exemplos A circunferência da figura tem raio igual a 9 cm e o comprimento do arco AB assinalado é 10,8 cm. Calcular, em radianos, a medida de AB. 9 cm B 10,8 cm O A  = comprimento R  = 10,8 cm 9 cm = 1,2 rad

49. Exemplos O arco AB da figura tem medida de 30º e o raio da circunferência é de 4 cm. Calcular, em cm, o comprimento do arco AB. 4 cm B 30º O A ângulo x x = 2  .4.30 360 comprimento 360º 2  R 30º 2  3 = ≈ 2, 1 cm

50. Exemplos Numa circunferência, o comprimento de um arco é de 40 cm. Esse mesmo arco mede 5 rad. Calcular a medida do raio da circunferência. R B 40 cm O A R  = comprimento R 5 = 40 cm R 5R = 40  ⇒ R = 8 cm

51. Arcos especiais 0 0 o Arco nulo  /2 90º Arco de ¼ de volta  180º Arco de meia-volta 2  360º Arco completo Medida em radianos Medida em graus Represen-tação O O O O

52. Transformando unidades As medidas de um arco em graus e radianos são proporcionais. Por isso podemos transformar uma unidade em outra por uma regra de três. 180º correspondem a  rad

53. Exemplos Transformar 72º em radianos. 2  5 180º  rad 72º x x = 72 .  180 = rad

54. Exemplos Exprimir rad em graus. 5. 180  rad equivale a 180º. x = 4 = 225º 5.  4 = 5  4