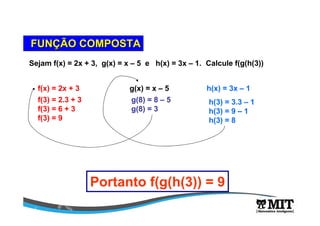
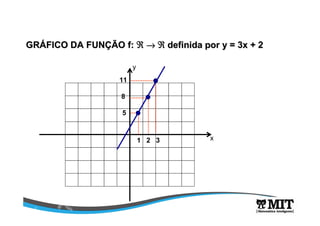
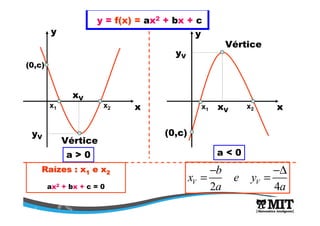
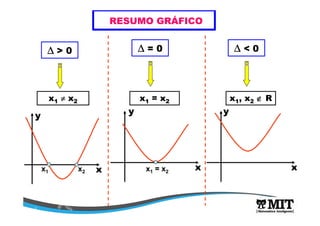
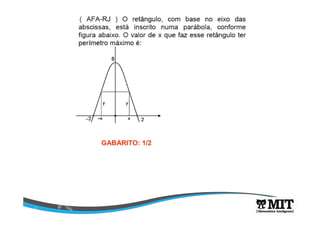
A função que representa a altura do projétil é uma função quadrática da forma y = f(x) = ax2 + bx + c. Sua análise permite determinar que a altura máxima é de 10m quando t = 10s, correspondendo ao vértice da parábola. O domínio da função é [0,20] de acordo com o enunciado.

1. www.ricardinhomatematica.com.brwww.ricardinhomatematica.com.br
FUNFUNÇÇÕESÕES

2. P
x
y
O
y
x
P(x, y)
abscissa do
ponto P
ordenado do
ponto P
No caso, x e y são as
coordenadas de P.

3. xO
y
E
A
F
B
C D
E (x, 0)
A (+, +)
F (0, y)
B (–, +)
C (–, –)
D (+, –)

4. FUNFUNÇÇÃOÃO
DEFINIDEFINIÇÇÃOÃO
Sejam A e B dois conjuntos não vazios e uma relaSejam A e B dois conjuntos não vazios e uma relaçção R de Aão R de A
em B, essa relaem B, essa relaçção serão seráá chamada de funchamada de funçção quandoão quando parapara
todotodo e qualquer elemento de A estiver associado ae qualquer elemento de A estiver associado a umum úúniconico
elemento em B.elemento em B.
A
BA B
NÃONÃO ÉÉ FUNFUNÇÇÃOÃO NÃONÃO ÉÉ FUNFUNÇÇÃOÃO
A B
ÉÉ FUNFUNÇÇÃOÃO

5. FUNFUNÇÇÃOÃO
DEFINIDEFINIÇÇÃOÃO
Sejam A e B dois conjuntos não vazios e uma relaSejam A e B dois conjuntos não vazios e uma relaçção R de Aão R de A
em B, essa relaem B, essa relaçção serão seráá chamada de funchamada de funçção quandoão quando parapara
todotodo e qualquer elemento de A estiver associado ae qualquer elemento de A estiver associado a umum úúniconico
elemento em B.elemento em B.
A relaA relaçção binão bináária h = {(x;y)| x > y}ria h = {(x;y)| x > y}
y>x
A
B
2
4
1
3
5
h: {(2;1), (4;1), (4,3)}h: {(2;1), (4;1), (4,3)}
A relaA relaçção binão bináária g = {(x;y)| y= x + 3}ria g = {(x;y)| y= x + 3}
3xy +=
2
4
1
3
5
g: {(2;5)}g: {(2;5)}
A B
NÃONÃO ÉÉ FUNFUNÇÇÃOÃO NÃONÃO ÉÉ FUNFUNÇÇÃOÃO

6. c) A relac) A relaçção binão bináária f = {(x;y)| y = x + 1}ria f = {(x;y)| y = x + 1}
1+= xy
A B2
4
1
3
5
f: {(2;3), (4;5)}f: {(2;3), (4;5)}
ff éé uma funuma funçção de A em B, poisão de A em B, pois todotodo
elemento de A estelemento de A estáá associado aassociado a umum
úúniconico elemento em Belemento em B
ELEMENTOS DE UMA FUNELEMENTOS DE UMA FUNÇÇÃO: f: AÃO: f: A →→→→→→→→ BB
DOMDOMÍÍNIO: A = {2, 4}NIO: A = {2, 4}
CONTRA DOMCONTRA DOMÍÍNIO: B = {1, 3, 5}NIO: B = {1, 3, 5}
CONJUNTO IMAGEM: Im (f) = {3, 5}CONJUNTO IMAGEM: Im (f) = {3, 5}

7. x
y
0 1 2 3 4
Não é função

8. Não é função

9. x
y
0 1 2 3 4
É função

10. Considere a funConsidere a funçção f: Aão f: A →→→→→→→→ B definida porB definida por y = 3x + 2, podey = 3x + 2, pode--sese
afirmar que o conjunto imagem de fafirmar que o conjunto imagem de f éé::
23 += xy
A B 23 += xy
521.3 =+=y1
2
3
5
8
11
15
17
822.3 =+=y
1123.3 =+=y
23)( += xxf
→
→
→
5)1( =f
8)2( =f
11)3( =f
}11,8,5{)Im( =∴ f

11. GRGRÁÁFICO DA FUNFICO DA FUNÇÇÃO f: AÃO f: A →→→→→→→→ B definida por y = 3x + 2B definida por y = 3x + 2
Pares Ordenados Obtidos: {(1,5); (2,8); (3,11)}Pares Ordenados Obtidos: {(1,5); (2,8); (3,11)}
1 2 3
11
8
5
x
y

12. 1 2 3
11
8
5
x
y
GRGRÁÁFICO DA FUNFICO DA FUNÇÇÃO f:ÃO f: ℜℜℜℜℜℜℜℜ →→→→→→→→ ℜℜℜℜℜℜℜℜ definida por y = 3x + 2definida por y = 3x + 2

13. x
y
0
2
4 10
8
D = [4, 10[
Im = [2, 8[
D = {x ∈ℜ∈ℜ∈ℜ∈ℜ/4 ≤≤≤≤ x < 10}
Im = {y ∈ℜ∈ℜ∈ℜ∈ℜ/2 ≤≤≤≤ y < 8}
Domínio
Imagem

14. Seja o gráfico abaixo da função f, determinar a soma dos números associados às
proposições VERDADEIRAS:
01. O domínio da função f é {x ∈ R | - 3 ≤ x ≤ 3}
02. A imagem da função f é {y ∈ R | - 2 ≤ y ≤ 3}
04. para x = 3, tem-se y = 3
08. para x = 0, tem-se y = 2
16. para x = - 3, tem-se y = 0
32. A função é decrescente em todo seu domínio
V
V
(3,3) ou f(3) = 3
(0,2) ou f(0) = 2
(-3,2) ou f(-3) = 2
V
V
F
F

15. Dado que f(1) = 2 e, para todo x, f(x) = 5 f(x – 1), obtenha:
a) f(2)
b) f(3)
c) f(0)
d) f(– 1)
Resposta: 220000 == bea

16. Resposta: 12

18. www.ricardinhomatematica.com.brwww.ricardinhomatematica.com.br
FUNFUNÇÇÃO POLINOMIAL DO 1ÃO POLINOMIAL DO 1ºº GRAUGRAU

19. y = f(x) = ax + b
a > 0
y
D = ℜℜℜℜ Im = ℜℜℜℜ
FUNÇÃO
CRESCENTE
(0, b)
x
y
(0, b)
x
FUNÇÃO
DECRESCENTE
a < 0
Raiz ou
zero da
função
y = 0

20. y = x – 2
y
(0, -2)
x2 3
1
4
2
5
3
y = 3x – 6 y
(0, -6)
x2 3
3
4
6
5
9
CÁLCULO DO COEFICIENTE ANGULAR – TAXA DE VARIAÇÃO
∆x
∆y
a =

21. Seja f(x) = ax + b. Sabe-se que f(3) = 5 e f(-1) = - 3. Dê o valor de f(8).
f(3) = 5
f(-1) = -3
(3, 5)
(-1, -3)
y = ax + b
5 = a(3) + b
-3 = a(-1) + b



=+
=+
3-ba-
5b3a
a = 2 b = - 1
f(x) = ax + b
f(x) = 2x – 1
Logo: f(8) = 2.8 – 1 f(8) = 15

22. Sabe-se que o valor de um carro novo é R$ 30 000,00 e, com 4 anos de uso, passa
a ser R$ 20 000,00. Considerando o decrescimento linear, obtenha o valor desse
carro depois de 8 anos de uso.
x(anos)
y(reais)
0 4
30 000
20 000
Função do 1º grau:
f(x) = a.x+ b
P1(0,30000)
P2(4,20000)
30000 = a.0 + b
b = 30000
20000 = a. 4 + 30000
a = -2500
f(x) = a.x+ b
f(x) = -2500x+ 30000
f(8) = -2500.8+ 30000
f(8)f(8) == 10 00010 000
Portanto após 8 anos o
valor do carro será R$ 10000,00
y = a.x+ b
y = a.x+ b

23. O valor de uma máquina decresce linearmente com o tempo, devido ao desgaste.
Sabendo-se que hoje ela vale R$800,00, e que daqui a 5 anos valerá R$160,00,
o seu valor, em reais, daqui a três anos será:
x(anos)
y(reais)
0 5
160
800
Função do 1º grau:
f(x) = a.x+ b
P1(0,800)
P2(5,160)
800 = a.0 + b
b = 800
160 = a. 5 + 800
-640 = 5a
a = -128
f(x) = a.x+ b
f(x) = -128.x+ 800
f(3) = -128.3+ 800
f(3)f(3) == 416416
Portanto após 3 anos a
Máquina valerá R$ 416,00

24. A semi-reta representada no gráfico seguinte expressa o custo de produção C,
em reais, de n quilos de certo produto.
C(reais)
x(quilogramas)0 20
80
180
Se o fabricante vender esse
produto a R$ 102,00 o quilo,
a sua porcentagem de lucro
em cada venda será?
Função do 1º grau:
f(x) = a.x+ b
P1(0,80)
P2(20,180)
80 = a.0 + b
b = 80
180 = a. 20 + 80
20a = 100
a = 5
f(x) = a.x+ b
f(x) = 5.x+ 80
f(1) = 5.1+ 80 ⇒⇒ f(1) = 85f(1) = 85
R$ 85 ⇔ 100%
R$102 ⇔ x
x = 120%
LUCRO DE 20%

26. Um camponês adquire um moinho ao preço de R$860,00. Com o passar do tempo,
ocorre uma depreciação linear no preço desse equipamento. Considere que, em 6
anos, o preço do moinho será de R$ 500,00. Com base nessas informações, é correto
afirmar:
x(anos)
y(reais)
0 6
500
860
Função do 1º grau:
f(x) = a.x+ b
A(0,860)
B(6,500)
860 = a.0 + b
b = 860
500 = a. 6 + 860
-360 = 6a
a = -60
f(x) = a.x+ b
f(x) = -60.x+ 860
a) f(3) = -60.3+ 860
f(3) = 680
A
B
F
b) f(9) = -60.9+ 860
f(9) = 320
F
c) f(7) = -60.7+ 860
f(7) = 440
F
d) - 60x + 860 < 200
-60x < -660
x > 11anos
F
e) f(13) = -60.13+ 860
f(13) = 440
f(13) = 80
V

27. Em um termômetro de mercúrio, a temperatura é uma função afim (função do 1o
grau) da altura do mercúrio. Sabendo que as temperaturas 0oC e 100oC
correspondem, respectivamente, às alturas 20 ml e 270 ml do mercúrio, então a
temperatura correspondente a 112,5 ml é
ml
temperatura0 100
20
270
Função do 1º grau:
f(x) = a.x+ b
P1(0,20)
P2(100,270)
20 = a.0 + b
b = 20
270 = a. 100 + 20
100a = 250
a = 2,5
f(x) = a.x+ b
f(x) = 2,5.x+ 20
y = 2,5x + 20
112,5 = 2,5x + 20
92,5=2,5x
37°C = x

28. www.ricardinhomatematica.com.brwww.ricardinhomatematica.com.br
FUNFUNÇÇÃO POLINOMIAL DO 2ÃO POLINOMIAL DO 2ºº GRAUGRAU

29. y = f(x) = ax2 + bx + c
Vértice
(0,c)
xV
yV
x1 x2
Vértice
(0,c)
xV
yV
x1 x2
y
x x
y
a > 0 a < 0
RaRaíízeszes : x: x11 ee xx22
ax2 + bx + c = 0 2 4
V V
b
x e y
a a
− −∆
= =

30. RESUMO GRÁFICO
∆∆∆∆ > 0
x1 ≠≠≠≠ x2
x1 x2
y
x
∆∆∆∆ = 0
x1 = x2
x1 = x2
x
y
∆∆∆∆ < 0
x1, x2 ∉∉∉∉ R
x
y

31. DE OLHO NO VESTIBULARDE OLHO NO VESTIBULAR

32. Após o lançamento de um projétil, sua
altura h, em metros, t segundos após o
seu lançamento é dada por
h(t) = – t2 + 20t. Em relação a este
lançamento, analise as afirmações a
seguir.
l. A altura máxima atingida pelo projétil
foi de 10m.
ll. O projétil atingiu a altura máxima
quando t=10s.
lll. A altura do projétil é representada por
uma função polinomial quadrática cujo
domínio é [0,20].
lV. Quando t = 11, o projétil ainda não
atingiu sua altura máxima.
Todas as afirmações corretas estão em:
a) I – III b) I – II – IV c) II – III d) III – IV
ACAFE – SC PUC – PR
O lucro de uma determinada
empresa é dado pela lei
L(x) =L(x) = -- xx22 + 8+ 8xx -- 77, em que x é a
quantidade vendida (em milhares de
unidades) e L é o lucro (em reais). A
quantidade que se deve vender para
que o lucro seja máximo bem como
o valor desse lucro são,
respectivamente:
A) 3.000 unidades e R$ 6.000,00
B) 4.000 unidades e R$ 9.000,00
C) 4.000 unidades e R$ 8.000,00
D) 5.000 unidades e R$ 12.000,00
E) 4.500 unidades e R$ 9.000,00

33. UFSC – SC
Se o lucro de uma empresa é dado por
L(x) = 4(3 – x)(x – 2), onde x é a
quantidade vendida, então o lucro da
empresa é máximo quando x é igual a:
UFSC – SC
O lucro, em reais, para a comercialização
de x unidades de um determinado
produto é dado por
L(x) = - 1120 + 148x – x2. Então, para que
se tenha lucro máximo, deve-se vender
quantos produtos?
UFSC - SC
Tem-se uma folha de cartolina
com forma retangular, cujos lados
medem 56cm e 32cm e deseja-
se cortar as quinas, conforme
ilustração a seguir. Quanto
deve medir x, em centímetros,
para que a área da região
hachurada seja a maior possível?
GABARITO: 11

34. UFSC – SC

35. GABARITO: 1/2

36. www.ricardinhomatematica.com.brwww.ricardinhomatematica.com.br
PARIDADE DE FUNPARIDADE DE FUNÇÇÕESÕES

37. FUNFUNÇÇÃO PAR OUÃO PAR OU ÍÍMPARMPAR
FUNÇÃO PAR
VALORES SIMÉTRICOS DE X
IMAGENS IGUAIS
f(x) = x2 – 4
f(-3) = (-3)2 – 4 =
f(3) = (3)2 – 4 =
5
5
FUNÇÃO ÍMPAR
VALORES SIMÉTRICOS DE X
IMAGENS SIMÉTRICAS
f(x) = x3
f(-4) = (-4)3 =
f(4) = 43 =
- 64
64
f(-x) = f(x) f(-x) = - f(x)

38. FUNÇÃO PAR
VALORES SIMÉTRICOS DE X
IMAGENS IGUAIS
FUNÇÃO ÍMPAR
VALORES SIMÉTRICOS DE X
IMAGENS SIMÉTRICAS
f(-x) = f(x)
f(-x) = - f(x)
FUNFUNÇÇÃO PAR OUÃO PAR OU ÍÍMPAR?MPAR?
1) f(x) = 4x3 + x
GRÁFICO SIMÉTRICO AO EIXO Y
GRÁFICO SIMÉTRICO EM RELAÇÃO
A ORIGEM
2) f(x) = 3x4 + 5x2
3) f(x) = 5x4 + 2x3
4) f(x) = sen x
5) f(x) = cos x
6) f(x) = tg x
ÍÍMPARMPAR f(-x) = - f(x)
f(-2) = - f(2)
PARPAR f(-x) = f(x)
f(-3) = f(3)
SEMSEM
PARIDADEPARIDADE
ÍÍMPARMPAR sen(-x) = - sen(x)
sen(-30°) = - sen(30°)
PARPAR
cos(-x) = cos(x)
cos(-30°) = cos(30°)
ÍÍMPARMPAR tg(-x) = - tg(x)
tg(-30°) = - tg(30°)

39. DE OLHO NO VESTIBULARDE OLHO NO VESTIBULAR

40. UFSC 2013UFSC 2013
ff éé uma funuma funççãoão ÍÍMPAR?MPAR?
NÃO, POIS f(NÃO, POIS f(--2)2) ≠≠ --f(2)f(2)

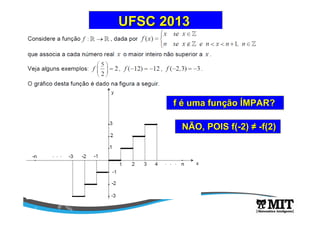
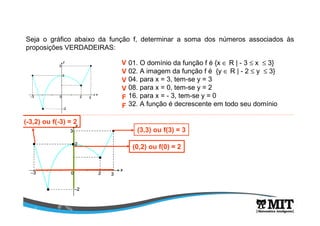
41. Observe o gráfico da função cujo domínio é o conjunto
D={x∈∈∈∈ R/- 2 < x < 4} e analise as afirmações a seguir.
ACAFE 2013.1ACAFE 2013.1
l. A função é par.
ll. A função possui 3 raízes reais.
lll. No intervalo A=[1,3] a função é
decrescente.
IV. A função pode ser representada por
y = x³ - 3x² - x +3, sendo
D={x∈∈∈∈ R/- 2 < x < 4}
Todas as afirmações corretas estão em:
a) I - II - III
b) II - IV
c) II - III - IV
d) III - IV

42. www.ricardinhomatematica.com.brwww.ricardinhomatematica.com.br
FUNFUNÇÇÃO COMPOSTAÃO COMPOSTA

43. ( ) 34xxg −= ( ) 12xxf +=
A B C
FUNFUNÇÇÃO COMPOSTAÃO COMPOSTA
f(g(x)) = fog (x)
g(f(x)) = gof (x)
f(f(x)) = fof(x)
g(g(x)) = gog(x)
NOTANOTAÇÇÕESÕES
2 5 11
( ) 5-8xg(x)f =
f(x) = 2x + 1
f(…) = 2(…) + 1
f(g(x)) = 2g(x) + 1
f(g(x)) = 2(4x – 3) + 1
CCÁÁLCULO de f(g(x))LCULO de f(g(x))
f(g(x)) = 8x – 5

44. FUNFUNÇÇÃO COMPOSTAÃO COMPOSTA
Sejam f(x) = 2x + 3, g(x) = x – 5 e h(x) = 3x – 1. Calcule f(g(h(3))
f(x) = 2x + 3 g(x) = x – 5 h(x) = 3x – 1
h(3) = 3.3 – 1
h(3) = 9 – 1
h(3) = 8
g(8) = 8 – 5
g(8) = 3
f(3) = 2.3 + 3
f(3) = 6 + 3
f(3) = 9
Portanto f(g(h(3)) = 9

45. DE OLHO NO VESTIBULARDE OLHO NO VESTIBULAR

46. O número N de caminhões produzidos em uma montadora durante um dia,
após t horas de operação, é dado por N(t) = 20t – t2, sendo que 0 ≤ t ≤ 10.
Suponha que o custo C (em milhares de reais) para se produzir N
caminhões seja dado por C(N) = 50 + 30N.
a) Escreva o custo C como uma função do tempo t de operação da
montadora.
b) Em que instante t, de um dia de produção, o custo alcançará o valor de
2300 milhares de reais?
UFPRUFPR –– 20132013 –– SEGUNDA FASESEGUNDA FASE

47. UFSCUFSC –– VERDADEIRO OU FALSOVERDADEIRO OU FALSO
Sejam f e g funções reais definidas por f(x) = sen x e g(x) = x2 + 1.
Então (fog)(x) = (fog)(– x) para todo x real.
UFSC 2012UFSC 2012
VV
Sejam h e k, duas funções, dadas por h(x) = 2x - 1 e k(x) = 3x + 2.
Então h(k(1)) é igual a 9.
UFSC 2002UFSC 2002
VV
UFSC 2006UFSC 2006
UFSCUFSC –– QUESTÃO ABERTAQUESTÃO ABERTA

48. www.ricardinhomatematica.com.brwww.ricardinhomatematica.com.br
FUNFUNÇÇÃO INJETORA SOBREJETORAÃO INJETORA SOBREJETORA
E BIJETORAE BIJETORA

49. FUNFUNÇÇÃO INJETORAÃO INJETORA
GRÁFICO ESTRITAMENTE CRESCENTE OU ESTRITAMENTE DECRESCENTE
FUNFUNÇÇÃO SOBREJETORAÃO SOBREJETORA
FUNFUNÇÇÃO BIJETORAÃO BIJETORA

50. DE OLHO NO VESTIBULARDE OLHO NO VESTIBULAR

51. UFSC 2013UFSC 2013
ff éé uma funuma funçção INJETORA?ão INJETORA?
NÃO, POIS f(2,3) =NÃO, POIS f(2,3) = f(2,7)f(2,7)

52. FUNFUNÇÇÃO INVERSAÃO INVERSA
3x
1-2x
f(x)
−
=
Encontre a inversa da função
3x
1-2x
f(x)
−
=
x =
3
12
−
−
y
y
x(y – 3) = 2y – 1
xy – 3x = 2y – 1
xy – 2y = 3x – 1
xy – 2y = 3x – 1
y(x – 2) = 3x – 1
y =
2
13
−
−
x
x
2x
13x
(x)f 1
−
−
=−
GABARITO: 27