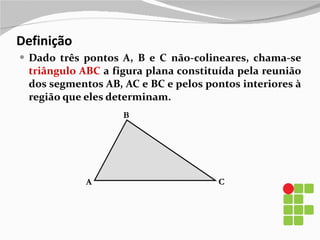
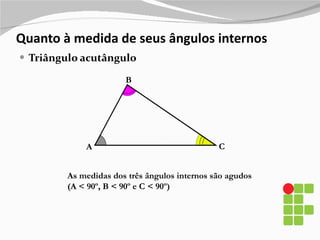
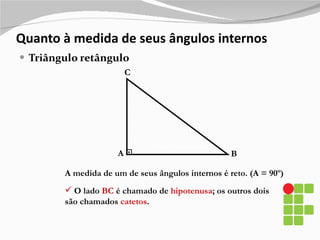
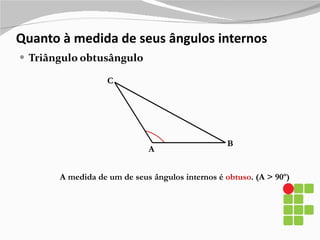
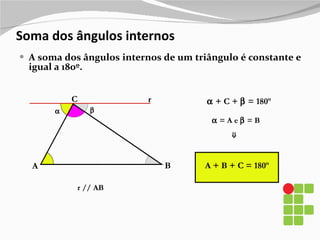
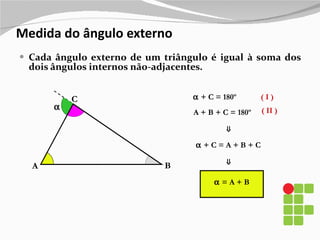
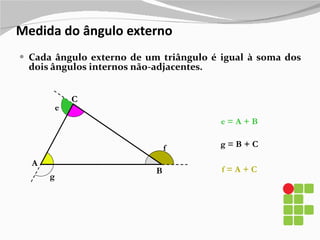
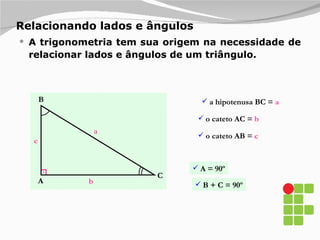
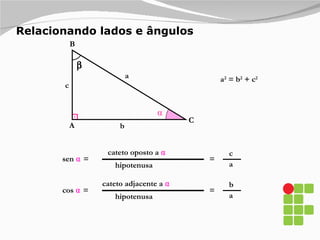
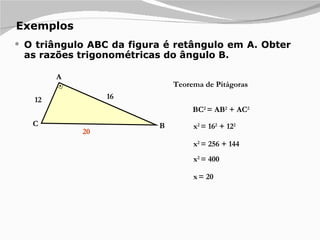
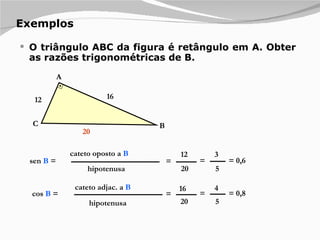
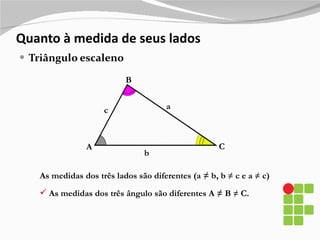
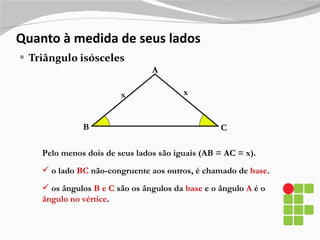
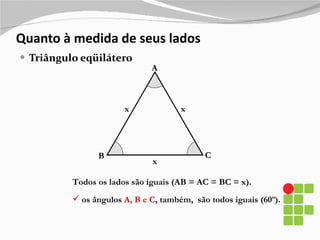
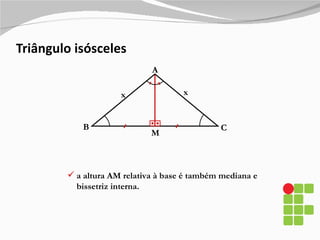
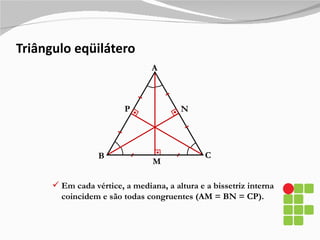
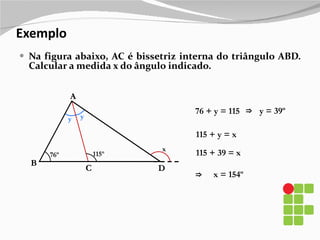
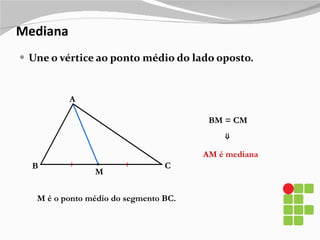
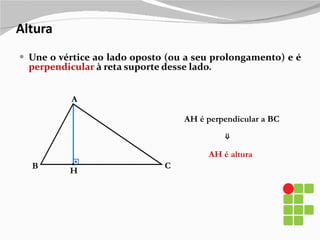
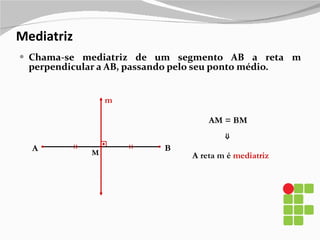
1) O documento apresenta os diferentes tipos de triângulos classificados de acordo com a medida de seus lados e ângulos internos. 2) São descritos os triângulos escaleno, isósceles, equilátero, agudo, retângulo e obtusângulo. 3) Também são explicados elementos como mediânas, alturas, bissetrizes e suas propriedades nos diferentes tipos de triângulos.

2. Definição Dado três pontos A, B e C não-colineares, chama-se triângulo ABC a figura plana constituída pela reunião dos segmentos AB, AC e BC e pelos pontos interiores à região que eles determinam. A B C

3. Elementos principais A figura mostra o triângulo ABC. Nele, destacamos A B C a b c os vértices A, B e C os lados e suas medidas: AB = c, AC = b e BC = a os ângulos internos A, B e C.  ângulo externo (  )

5. Quanto à medida de seus lados Triângulo escaleno A B C a b c As medidas dos três lados são diferentes (a ≠ b, b ≠ c e a ≠ c) As medidas dos três ângulo são diferentes A ≠ B ≠ C.

6. Quanto à medida de seus lados Triângulo isósceles A B C x x Pelo menos dois de seus lados são iguais (AB = AC = x). o lado BC não-congruente aos outros, é chamado de base . os ângulos B e C são os ângulos da base e o ângulo A é o ângulo no vértice .

7. Quanto à medida de seus lados Triângulo eqüilátero A B C x x Todos os lados são iguais (AB = AC = BC = x). os ângulos A, B e C , também, são todos iguais (60º). x

8. Quanto à medida de seus ângulos internos Triângulo acutângulo A B C As medidas dos três ângulos internos são agudos (A < 90º, B < 90º e C < 90º)

9. Quanto à medida de seus ângulos internos Triângulo retângulo A B C A medida de um de seus ângulos internos é reto. (A = 90º) O lado BC é chamado de hipotenusa ; os outros dois são chamados catetos .

10. Quanto à medida de seus ângulos internos Triângulo obtusângulo A B C A medida de um de seus ângulos internos é obtuso . (A > 90º)

12. Soma dos ângulos internos A soma dos ângulos internos de um triângulo é constante e igual a 180º. A C B  r  A + B + C = 180º  + C +  = 180º  = A e  = B ⇒ r // AB

13. Medida do ângulo externo Cada ângulo externo de um triângulo é igual à soma dos dois ângulos internos não-adjacentes.  A C B  + C = 180º A + B + C = 180º ( I ) ( II ) ⇒  + C = A + B + C ⇒  = A + B

14. Medida do ângulo externo Cada ângulo externo de um triângulo é igual à soma dos dois ângulos internos não-adjacentes. f A C B e = A + B g e f = A + C g = B + C

15. Exemplo Na figura abaixo, AC é bissetriz interna do triângulo ABD. Calcular a medida x do ângulo indicado. B A D 76º 115º C x y y 76 + y = 115 y = 39º ⇒ 115 + y = x 115 + 39 = x x = 154º ⇒

17. Mediana Une o vértice ao ponto médio do lado oposto. B A C M AM é mediana BM = CM ⇒ M é o ponto médio do segmento BC.

18. Altura Une o vértice ao lado oposto (ou a seu prolongamento) e é perpendicular à reta suporte desse lado. B A C H AH é altura AH é perpendicular a BC ⇒

19. Bissetriz interna Une o vértice ao lado oposto, dividindo o ângulo desse vértice em dois ângulos congruentes . B A C S AS é bissetriz

20. Mediatriz Chama-se mediatriz de um segmento AB a reta m perpendicular a AB, passando pelo seu ponto médio. A m B M A reta m é mediatriz AM = BM ⇒

21. Triângulo isósceles A B C x x a altura AM relativa à base é também mediana e bissetriz interna. M

22. Triângulo eqüilátero A B C N P Em cada vértice, a mediana, a altura e a bissetriz interna coincidem e são todas congruentes (AM = BN = CP). M

24. Relacionando lados e ângulos A trigonometria tem sua origem na necessidade de relacionar lados e ângulos de um triângulo. a hipotenusa BC = a A B C a b c o cateto AC = b o cateto AB = c A = 90º B + C = 90º

25. Relacionando lados e ângulos A B C a b c a 2 = b 2 + c 2 ⍺ cateto oposto a ⍺ hipotenusa = sen ⍺ = c a cateto adjacente a ⍺ hipotenusa = cos ⍺ = b a 

26. Relacionando lados e ângulos A B C a b c a 2 = b 2 + c 2 ⍺ cateto oposto a ⍺ = tg ⍺ = c b cateto adjacente a ⍺  os números sen ⍺ , cos ⍺ e tg ⍺ são chamadas de razões trigonométricas do ângulo ⍺ .

27. Exemplos O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas do ângulo B. 12 16 A B C Teorema de Pitágoras BC 2 = AB 2 + AC 2 x 2 = 16 2 + 12 2 x 2 = 256 + 144 x 2 = 400 x = 20 20

28. Exemplos O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B. cateto oposto a B hipotenusa sen B = = 12 20 = 3 5 = 0,6 cateto adjac. a B hipotenusa cos B = = 16 20 = 4 5 = 0,8 12 16 A B C 20

29. Exemplos O triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B. cateto oposto a B cateto adjac. a B tg B = = 12 16 = 3 4 = 0,75 12 16 A B C 20

30. Exemplos Calcular os ângulos agudos de um triângulo retângulo cujos lados medem 5 cm e 6 cm. 5 cm 16 6 cm x y tg y = 6 5 = 1,2 ⇒ y ≈ 50º x + y = 90º ⇒ x ≈ 40º

32. Ângulos complementares  A B C 5 4 3 ⍺ +  = 90º ⍺ tg ⍺ = 3 4 ⇒ Os ângulos ⍺ e  são complementares sen ⍺ = 3 5 cos ⍺ = 4 5 tg  = 4 3 sen  = 4 5 cos  = 3 5

33. Ângulos complementares  A B C a b c ⍺ +  = 90º ⍺ tg ⍺ = 1 tg  ⇒ Os ângulos ⍺ e  são complementares sen ⍺ = cos  cos ⍺ = sen 

35. Seno, co-seno e tangente de 30º, 45º e 60º. 1 tg ½ cos ½ sen 60º 45º 30º √ 2/2 √ 2/2 √ 3/2 √ 3/2 √ 3/3 √ 3

36. Exemplos A partir dos dados apresentados na figura, determinar as medidas indicadas por x e y. x 16 y 30º sen 30º = x 12 12 cm ⇒ x = 12 . 1/2 ⇒ x = 6 cm cos 30º = y 12 ⇒ x = 12 . √ 3 /2 ⇒ x = 6 √ 3 cm

37. Exemplos Os triângulos ABC e BCD da figura são retângulos em B, sendo conhecidos os ângulos BAC = 30º e BDC = 60º, além de AD = 2 cm. Calcular os valores de x, y e z. 30º A B C D x y z 2 cm 60º

38. Identidades trigonométricas A partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações. b/a c/a  A C B a c b ⍺ sen ⍺ cos ⍺ = = b a . a c = b c = tg ⍺ tg x = sen x cos x

39. Exemplos Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno e a tangente desse ângulo. sen 2 x + cos 2 x ⇒ 3 5 + 2 cos 2 x = 1 ⇒ 9 25 + cos 2 x = 1 ⇒ 9 25 – cos 2 x = 1 = 25 – 9 25 ⇒ cos x = = 16 25 ± 4/5 ⇒ cos x = 4/5

40. Exemplos Sabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, co-tangente, secante e a co-secante desse ângulo. tg x = sen x cos x = 3 5 4 5 = 3 4