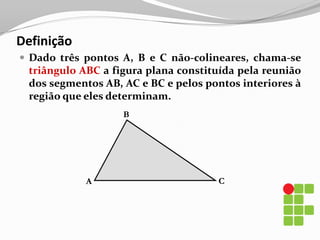
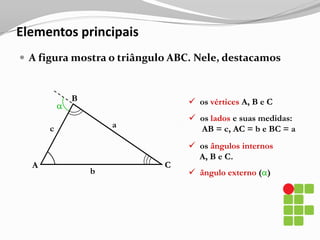
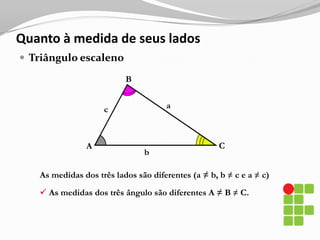
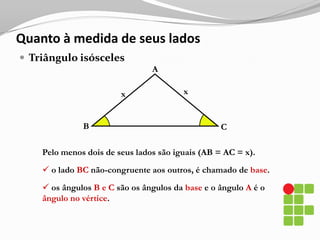
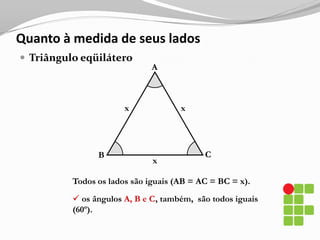
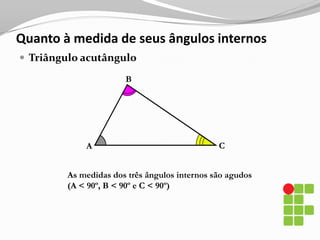
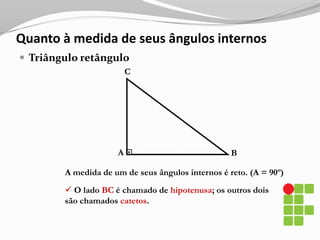
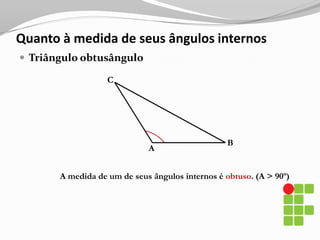
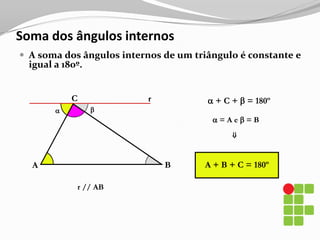
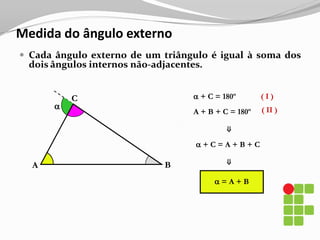
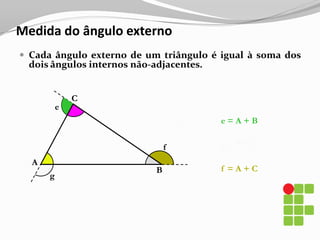
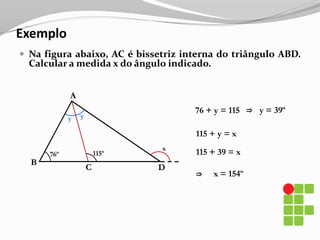
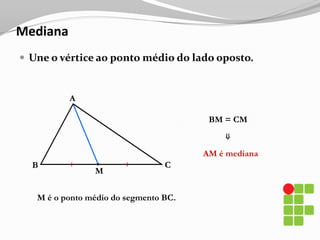
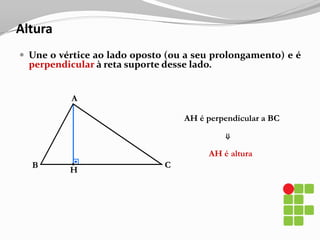
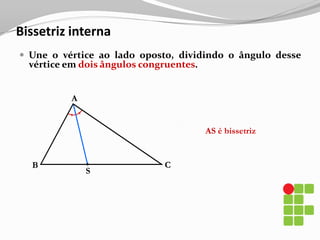
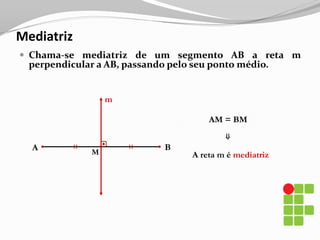
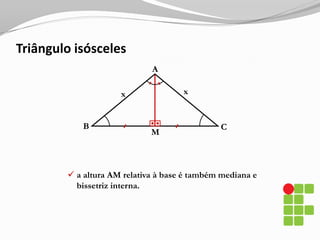
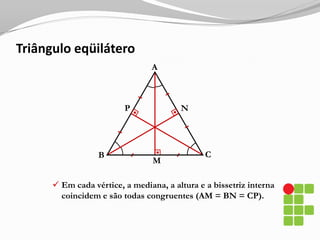
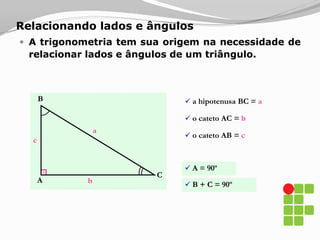
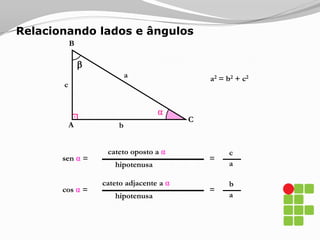
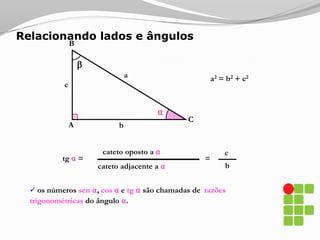
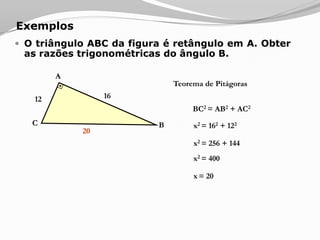
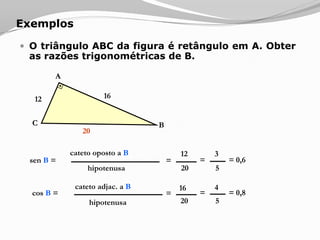
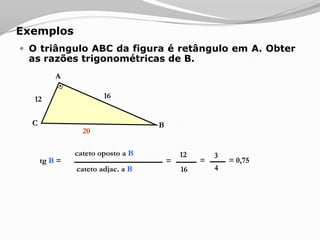
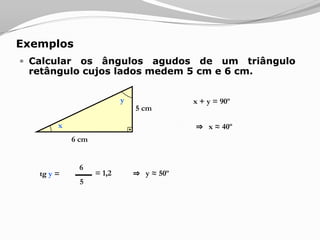
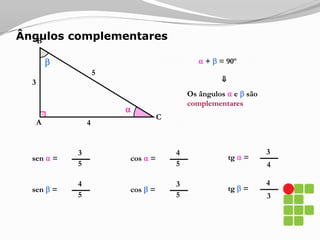
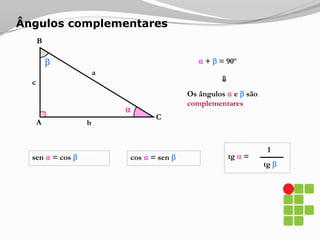
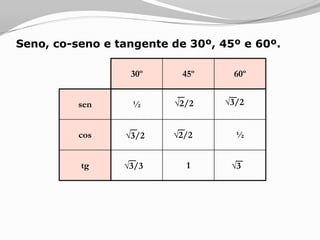
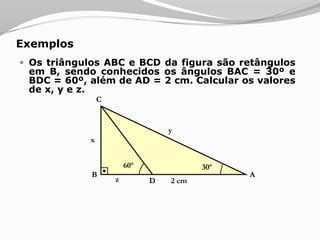
O documento apresenta os conceitos básicos sobre triângulos, incluindo definição, elementos, classificação de acordo com medidas de lados e ângulos, relações entre ângulos e segmentos notáveis. É introduzida a trigonometria no triângulo retângulo, relacionando lados e ângulos por meio de razões trigonométricas.

1. Estudo dos triângulos

2. DefiniçãoDado três pontos A, B e C não-colineares, chama-se triângulo ABC a figura plana constituída pela reunião dos segmentos AB, AC e BC e pelos pontos interiores à região que eles determinam.BCA

3. Elementos principaisA figura mostra o triângulo ABC. Nele, destacamosB os vértices A, B e C os lados e suas medidas: AB = c, AC = b e BC = aac os ângulos internos A, B e C.CAbângulo externo ()Classificação dos triângulos

4. Quanto à medida de seus ladosTriângulo escalenoBacCAbAs medidas dos três lados são diferentes (a ≠ b, b ≠ c e a ≠ c) As medidas dos três ângulo são diferentes A ≠ B ≠ C. Quanto à medida de seus ladosTriângulo isóscelesAxxBCPelo menos dois de seus lados são iguais (AB = AC = x). o lado BC não-congruente aos outros, é chamado de base.

5. os ângulos B e C são os ângulos da base e o ângulo A é o ângulo no vértice. Quanto à medida de seus ladosTriângulo eqüiláteroAxxCBxTodos os lados são iguais (AB = AC = BC = x). os ângulos A, B e C, também, são todos iguais (60º).Quanto à medida de seus ângulos internosTriângulo acutânguloBCAAs medidas dos três ângulos internos são agudos(A < 90º, B < 90º e C < 90º)

6. Quanto à medida de seus ângulos internosTriângulo retânguloCABA medida de um de seus ângulos internos é reto. (A = 90º) O lado BC é chamado de hipotenusa; os outros dois são chamados catetos.Quanto à medida de seus ângulos internosTriângulo obtusânguloCBAA medida de um de seus ângulos internos é obtuso. (A > 90º)

7. Ângulos no triângulo

8. Soma dos ângulos internosA soma dos ângulos internos de um triângulo é constante e igual a 180º.Cr + C +  = 180º = A e  = B⇒A + B + C = 180ºBAr // AB

9. Medida do ângulo externoCada ângulo externo de um triângulo é igual à soma dos dois ângulos internos não-adjacentes. + C = 180º( I )C( II )A + B + C = 180º⇒ + C = A + B + C⇒BA = A + B

10. Medida do ângulo externoCada ângulo externo de um triângulo é igual à soma dos dois ângulos internos não-adjacentes.Cee = A + Bg = B + CfAf = A + CBg

11. ExemploNa figura abaixo, AC é bissetriz interna do triângulo ABD. Calcular a medida x do ângulo indicado.A⇒y = 39º76 + y = 115yy115 + y = xx115 + 39 = x115º76ºBCD⇒x = 154º

12. Segmentos notáveis no triângulo

13. MedianaUne o vértice ao ponto médio do lado oposto.ABM = CM⇒AM é medianaCBMM é o ponto médio do segmento BC.

14. AlturaUne o vértice ao lado oposto (ou a seu prolongamento) e é perpendicular à reta suporte desse lado.AAH é perpendicular a BC⇒AH é alturaCBH

15. Bissetriz internaUne o vértice ao lado oposto, dividindo o ângulo desse vértice em dois ângulos congruentes.AAS é bissetrizCBS

16. MediatrizChama-se mediatriz de um segmento AB a reta m perpendicular a AB, passando pelo seu ponto médio.mAM = BM⇒BAMA reta m é mediatriz

17. Triângulo isóscelesAxxBCMa altura AM relativa à base é também mediana e bissetriz interna. Triângulo eqüiláteroANPCBMEm cada vértice, a mediana, a altura e a bissetriz interna coincidem e são todas congruentes (AM = BN = CP).Trigonometria no Triângulo Retângulo

18. Relacionando lados e ângulosA trigonometria tem sua origem na necessidade de relacionar lados e ângulos de um triângulo.B a hipotenusa BC = a

19. o cateto AC = ba o cateto AB = cc A = 90ºCAb B + C = 90ºRelacionando lados e ângulosBaa2 = b2 + c2c⍺CAbcateto oposto a ⍺c=sen ⍺ =ahipotenusacateto adjacente a ⍺b=cos ⍺ =ahipotenusa

20. Relacionando lados e ângulosBaa2 = b2 + c2c⍺CAbcateto oposto a ⍺ctg ⍺ ==bcateto adjacente a ⍺ os números sen⍺,cos⍺etg⍺são chamadas de razões trigonométricas do ângulo ⍺. ExemplosO triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas do ângulo B.ATeorema de Pitágoras1612BC2 = AB2 + AC2CBx2 = 162 + 12220x2 = 256 + 144x2 = 400x= 20

21. ExemplosO triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B.A1612CB20cateto oposto a B123== 0,6sen B ==205hipotenusacateto adjac. a B416== 0,8cos B ==205hipotenusa

22. ExemplosO triângulo ABC da figura é retângulo em A. Obter as razões trigonométricas de B.A1612CB20cateto oposto a B123== 0,75tg B ==4cateto adjac. a B16

23. ExemplosCalcular os ângulos agudos de um triângulo retângulo cujos lados medem 5 cm e 6 cm.yx + y = 90º165 cmx⇒ x ≈ 40º6 cm6= 1,2⇒ y ≈ 50ºtg y =5

24. Seno, Cosseno e Tangente de Ângulos Complementares

25. Ângulos complementaresB⍺ +  = 90º5⇒3Os ângulos ⍺ e  são complementares⍺CA4334tg ⍺ =sen ⍺ =cos ⍺ =554443tg  =sen  =cos  =553

26. Ângulos complementaresB⍺ +  = 90ºa⇒cOs ângulos ⍺ e  são complementares⍺CAb1tg ⍺ =sen ⍺ = cos cos ⍺ = sen tg 

27. Seno, Cosseno e Tangente de Ângulos Notáveis

28. Seno, co-seno e tangente de 30º, 45º e 60º.60º 45º 30º ½ sen√3/2√2/2½ cos√2/2√3/21tg√3/3√3

29. ExemplosA partir dos dados apresentados na figura, determinar as medidas indicadas por x e y.12 cm16x30ºyx⇒ x = 12 . 1/2⇒ x = 6 cmsen 30º =12y⇒ x = 12 . √3/2⇒ x = 6 √3 cmcos 30º =12

30. ExemplosOs triângulos ABC e BCD da figura são retângulos em B, sendo conhecidos os ângulos BAC = 30º e BDC = 60º, além de AD = 2 cm. Calcular os valores de x, y e z.Cyx60º30ºABzD2 cm

31. Identidades trigonométricasA partir do triângulo retângulo abaixo vamos deduzir algumas dessas relações.Csen xatg x =bcos x⍺BAcb/asen ⍺bab.=== tg ⍺=c/acos ⍺acc

32. ExemplosSabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno e a tangente desse ângulo. sen2 x + cos2 x23⇒cos2 x = 1+59⇒cos2 x = 1+2525 – 9916⇒cos2 x = 1==–252525⇒⇒cos x =± 4/5cos x = 4/5

33. ExemplosSabendo-se que o seno de um ângulo agudo é igual a 3/5, determine o co-seno, tangente, co-tangente, secante e a co-secante desse ângulo. 3sen x35tg x ===4cos x45