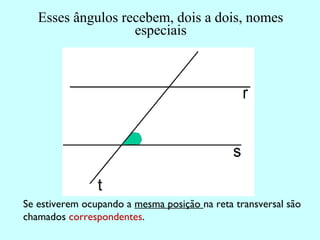
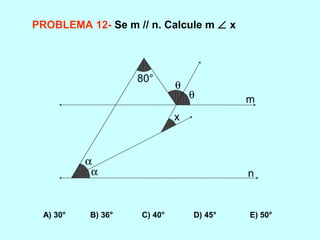
1) O documento apresenta os conceitos básicos de ângulos, incluindo classificação segundo medida, soma, posição e propriedades formadas por duas retas paralelas cortadas por uma transversal. 2) São mostrados exemplos de problemas envolvendo ângulos e suas propriedades, com resoluções detalhadas. 3) O documento termina com uma lista de exercícios sobre ângulos para fixação dos conceitos apresentados.

1. Profº: Antônio SoaresAntônio Soares
MATEMÁTICAMATEMÁTICA
Série: 8º anoSérie: 8º ano
Aula: – ÂNGULOSAula: – ÂNGULOS

2. β αO
A
B
ELEMENTOS DE UM ÂNGULO:
IntroduçãoIntrodução
Denomina-se ângulo a união de duas semirretas que
têm a mesma origem com uma das regiões do plano por
elas limitada.
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

3. α
0º < α < 180º0º < α < 180º
0º < β < 90º0º < β < 90ºβ
CLASSIFICAÇÃO SEGUNDO A SUA MEDIDA
a) ÂNGULO CONVEXO
a.1) ÂNGULO AGUDO
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

4. θ = 90ºθ = 90º
α
90º < α < 180º90º < α < 180º
θ
a.2) ÂNGULO RETO
a.3) ÂNGULO OBTUSO
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

5. α + β = 90ºα + β = 90º
θ + δ = 180ºθ + δ = 180º
δθ
α
β
CLASSIFICAÇÃO SEGUNDO A SOMA
a) ÂNGULOS COMPLEMENTARES
b) ÂNGULOS SUPLEMENTARES
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

6. α
β
δ ε
φ
α α
CLASSIFICAÇÃO SEGUNDO A SUA POSIÇÃO
a) ÂNGULOS ADJACENTES b) ÂNGULOS CONSECUTIVOS
ÂNGULOS OPOSTOS PELO VÉRTICE
são congruentes
Pode formar mais ângulosUn lado comum
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

7. Quantos ângulos temos aqui?
Isso mesmo, temos oito ângulos!

8. Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois,
nomes especiais

9. Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais

10. Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais

11. Se estiverem ocupando a mesma posição na reta transversal são
chamados correspondentes.
Esses ângulos recebem, dois a dois, nomes
especiais

12. Ângulos alternos internos

13. Ângulos alternos internos

14. Ângulos alternos externos

15. Ângulos alternos externos
Duas retas paralelas, cortadas por uma transversal determinam
ângulos alternos internos ou externos congruentes.

16. Exercício
Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 2x + 10º = x + 30º, cujo resultado é x
= 20º.

17. Ângulos colaterais internos

18. Ângulos colaterais internos

19. Ângulos colaterais externos

20. Ângulos colaterais externos
Duas retas paralelas, cortadas por uma transversal determinam
ângulos colaterais internos ou externos suplementares.

21. Exercício
Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação x + 20º = 180º, cujo resultado é
x = 160º.

22. Exercício
Qual a medida dos ângulos indicados?
Eles estão em que posição em relação à reta transversal?
O que podemos afirmar em relação às suas medidas?
Assim, precisamos resolver a equação 2x + x = 180º, cujo resultado é
x = 60º.

23. Exercício
Qual a medida dos ângulos indicados?
Os ângulos são concorrentes,
logo são ângulos iguais.
3b - 11° = 2b + 6°
3b - 2b = 6° + 11°
b = 17°
Os ângulos são suplementares, logo a soma entre eles é igual a 180°.
a + (2b + 6°) = 180°
a + 2b + 6° = 180°
a + 2(17°) + 6° = 180°(substituímos b por 17°)
a + 34° + 6° = 180°
a + 40° = 180°
a = 180° - 40°
a = 140°

24. 01. Ângulos alternos internos:
m ∠3 = m ∠5; m ∠4 = m ∠6
02. Ângulos alternos externos:
m ∠1 = m ∠7; m ∠2 = m
∠8
03. Ângulos conjugados internos:
m ∠3+m ∠6=m ∠4+m ∠5=180°
04. Ângulos conjugados externos:
m ∠1+m ∠8=m ∠2+m ∠7=180°
05. Ângulos correspondentes:
m ∠1 = m ∠5; m ∠4 = m ∠8
m ∠2 = m ∠6; m ∠3 = m ∠7
ÂNGULOS FORMADOS POR DUAS RETAS PARALELAS
E UMA TRANSVERSAL
1 2
34
5 6
78
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

25. α + β + θ = x + yα + β + θ = x + y
α
β
θ
x
y
01- Ângulos que se formam por uma linha poligonal entre
duas retas paralelas.
PROPRIEDADES DOS ÂNGULOS
GEOMETRIA: ÂNGULOSGEOMETRIA: ÂNGULOS
Série: 8º anoSérie: 8º ano

26. α
β
θ
δ
ε
α + β + θ + δ + ε = 180°α + β + θ + δ + ε = 180°
02- ÂNGULOS ENTRE DUAS RETAS PARALELAS

27. α + β = 180°α + β = 180°
α β
03- ÂNGULOS DE LADOS PERPENDICULARES

29. O complemento da diferença entre o suplemento e o
complemento de um ângulo “X” é igual ao dobro
do complemento do ângulo “X”. Calcule a medida do
ângulo “X”.
90 - { ( ) - ( ) } = ( )180° - X 90° - X 90° - X2
90° - { 180° - X - 90° + X } = 180° - 2X
90° - 90° = 180° - 2X
2X = 180° X = 90°X = 90°
RESOLUÇÃO
Problema Nº 01
A estrutura segundo o enunciado:
Desenvolvendo se obtem:
Logo se reduz a:

30. A soma das medidas dos ângulos é 80° e o
complemento do primeiro ângulo é o dobro da
medida do segundo ângulo. Calcule a diferença
das medidas desses ângulos.
Sejam os ângulos: α e β
α + β = 80°Dado: β = 80° - α ( 1 )
( 90° - α ) = 2β ( 2 )
Substituindo (1) em (2):
( 90° - α ) = 2 ( 80° - α )
90° - α = 160° -2α
β = 10°
α = 70°
α - β = 70°-10°
= 60°
Problema Nº 02
RESOLUÇÃO
Dado:
Diferença das medidas
Resolvendo

31. A soma de seus complementos dos ângulos é 130°
e a diferença de seus suplementos dos mesmos
ângulos é 10°. Calcule a medida destes ângulos.
Sejam os ângulos: α e β
( 90° - α ) ( 90° - β ) = 130°+
β + α = 50° ( 1 )
( 180° - α ) ( 180° - β ) = 10°-
β - α = 10° ( 2 )
Resolvendo: (1) e (2)
β + α = 50°
β - α = 10°
(+)
2β = 60°
β = 30°
α = 20°
Problema Nº 03
RESOLUÇÃO
Do enunciado:
Do enunciado:

32. Se têm ângulos adjacentes AOB e BOC
(AOB<BOC), se traça a bissetriz OM dol ângulo
AOC; se os ângulos BOC e BOM medem 60° e 20°
respectivamente. Calcule a medida do ângulo AOB.
A B
O
C
M
α
α
60°
20°X
Da figura:
α = 60° - 20°
Logo:
X = 40° - 20°
α = 40°
X = 20°X = 20°
Problema Nº 04
RESOLUÇÃO

33. A diferença das medidas dos ângulos adjacentes
AOB e BOC é 30°. Calcule a medida do ângulo
formado pela bissetriz do ângulo AOC com o lado
OB.
A
O
B
C
θ
θ
X
(θ- X)
( θ + X) (θ - X)= 30º
2X=30º
X = 15°X = 15°
Problema Nº 05
RESOLUÇÃO
M
Construção do gráfico segundo o
enunciado
Do enunciado:
AOB - OBC = 30°
-
Logo se substitui pelo que
se observa no gráfico

34. Se têm os ângulos consecutivos AOB, BOC e COD
tal que a m∠AOC = m∠BOD = 90°. Calcule a
medida do ângulo formado pelas bissetrizes dos
ângulos AOB e COD.
A
C
B
D
M
N
αα
β
β
θ
X
Da figura:
2α + θ = 90°
θ + 2β = 90°
( + )
2α + 2θ + 2β = 180°
α + θ + β = 90°
X = α + θ + βX = α + θ + β
X = 90°X = 90°
Problema Nº 06
RESOLUÇÃO
Construção do gráfico segundo o enunciado

35. Se m // n . Calcule a medida do ângulo “X”
80°
30°
α
α
θ
θ
X
m
n
Problema Nº 07

36. 2α + 2θ = 80° + 30°
Pela propriedade
Propriedade do quadrilátero
côncavo
α + θ = 55° (1)
80° = α + θ + X (2)
Substituindo (1) em (2)
80° = 55° + X
X = 25°X = 25°
80°
30°
α
α
θ
θ
X
m
n
RESOLUÇÃO

37. Se m // n . Calcular a medida do ângulo “X”
5α
4α 65°
X
m
n
Problema Nº 08

38. 5α
4α 65°
X
m
n
Pela propiedad:
4α + 5α = 90°
α = 10°α = 10°
Ângulo exterior do triângulo
40° 65°
X = 40° + 65°
X = 105°X = 105°
RESOLUÇÃO

39. Se m // n . Calcule a medida do ângulo ”X”
α
2α
x
m
n
θ
2θ
Problema Nº 09

40. 3α + 3θ = 180°
α + θ = 60°α + θ = 60°
Ângulos entre línhas poligonais
X = α + θ X = 60°X = 60°
RESOLUÇÃO
α
2α
x
m
n
θ
2θ
x
Ângulos conjugados
internos

42. PROBLEMA 01- Se L1 // L2 . Calcule a m ∠ x
A) 10° B) 20° C) 30° D) 40° E) 50°
x
α
α
β
β
4x
3x
L1
L2

43. m
n
30°
X
PROBLEMA 02- Se m // n. Calcule a m ∠ x
A) 18° B) 20° C) 30° D) 36° E) 48°

44. PROBLEMA 03- Se m // n. Calcule a m ∠ α
A) 15° B) 22° C) 27° D) 38° E) 45°
3α
3α
3α
α
m
n

45. PROBLEMA 04- Se m // n. Calcule o valor de “x”
A) 10° B) 15° C) 20° D) 25° E) 30°
40°
95°
α
α
2x
m
n

46. PROBLEMA 05- Calcule m ∠ x
A) 99° B) 100° C) 105° D) 110° E) 120°
3α
6α
x

47. α
4θ
4α
θ
X
m
n
PROBLEMA 06- Se m // n. Calcule m ∠ x
A) 22° B) 28° C) 30° D) 36° E) 60°

48. A) 24° B) 25° C) 32° D) 35° E) 45°
PROBLEMA 07- Se. Calcule m ∠ x
88°
24°
x
α
α
θ
θ
m
n

49. PROBLEMA 08- Se m // n. Calcule m ∠ x
20°
30°
X
m
n
A) 50° B) 60° C) 70° D) 80° E) 30°

50. PROBLEMA 09- Se m//n e θ - α = 80°. Calcule m∠x
A) 60° B) 65° C) 70° D) 75° E) 80°
θ
θ
x
α
α
m
n

51. PROBLEMA 10- Se m // n. Calcule m ∠ x
A) 20° B) 30° C) 40° D) 50° E) 60°
x
x
x
m
n

52. PROBLEMA 11- Se m // n. Calcule m ∠ α
A) 46° B) 48° C) 50° D) 55° E) 60°
180°-2α
α
2α
m
n

53. PROBLEMA 12- Se m // n. Calcule m ∠ x
A) 30° B) 36° C) 40° D) 45° E) 50°
α
α
θ
θ
x
80°
m
n

54. PROBLEMA 13- Se m // n. Calcule m ∠ x
A) 30° B) 40° C) 50° D) 60° E) 70°
80°
α
α
β
β
m
n
x

55. REPOSTAS DOS PROBLEMAS PROPOSTOS
1. 20º 8. 50º
2. 30º 9. 80º
3. 45º 10. 30º
4. 10º 11. 60º
5. 120º 12. 40º
6. 36º 13. 50º
7. 32º