Baixado 384 vezes
Carregado porHerlan Ribeiro de Souza
Geometria plana
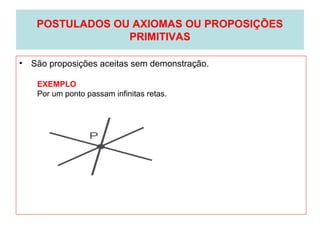
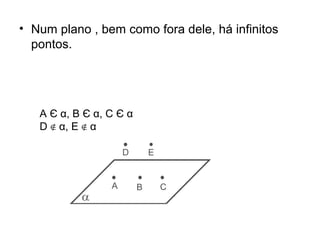
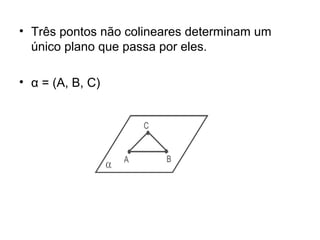
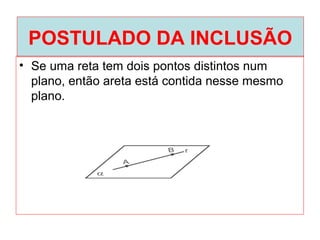
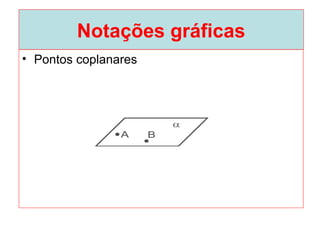
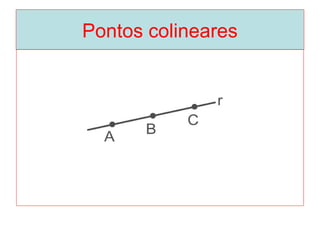
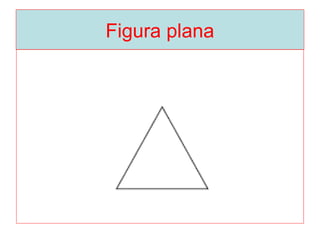
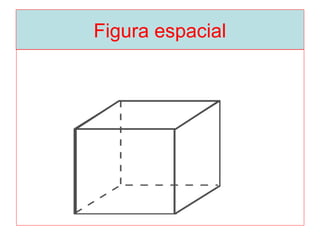
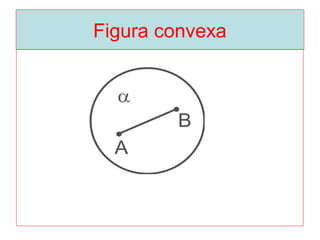
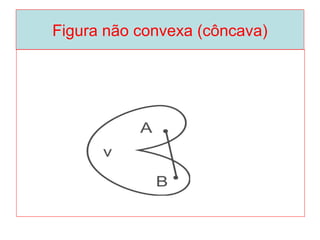
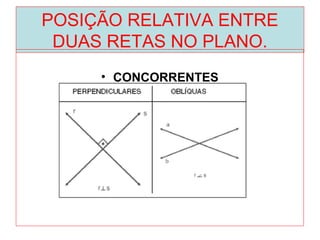
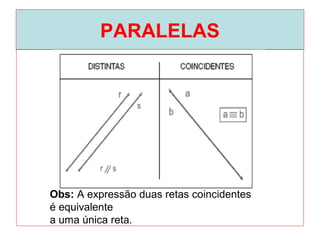
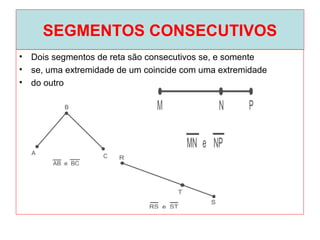
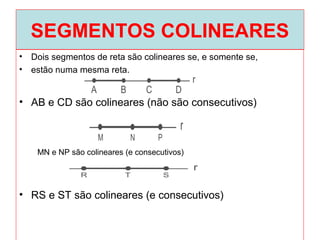
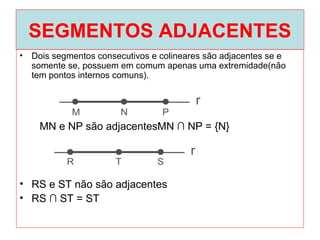
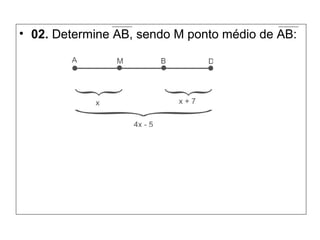
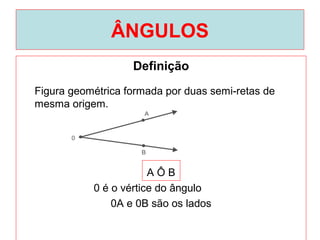
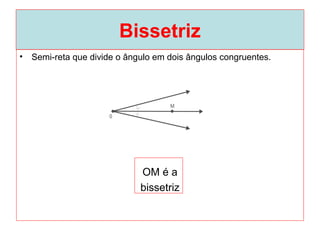
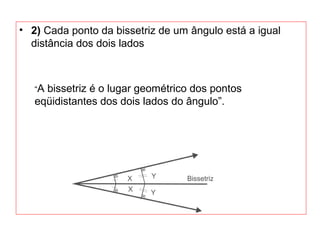
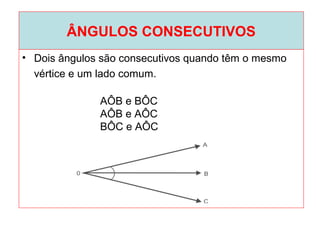
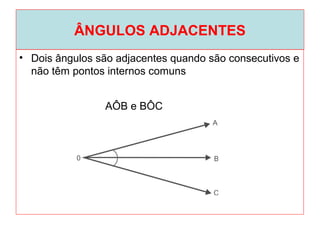
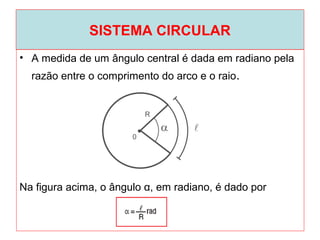
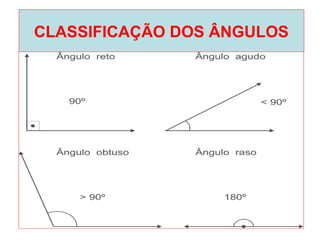
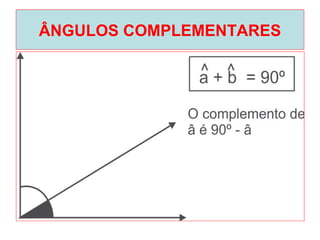
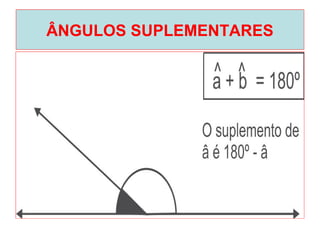
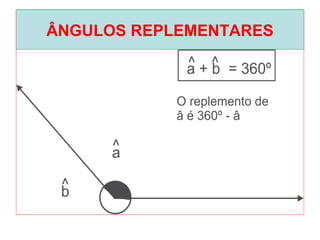
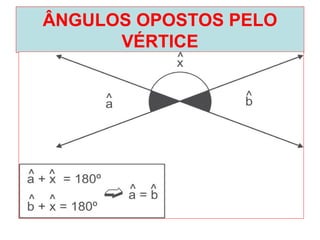
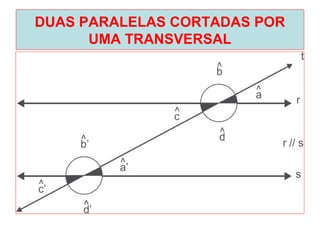
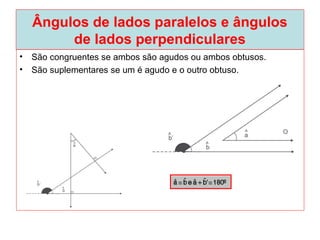
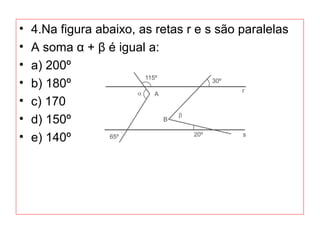
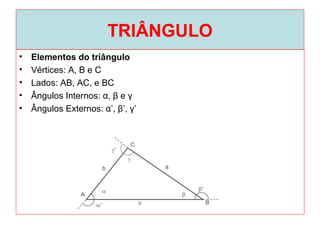
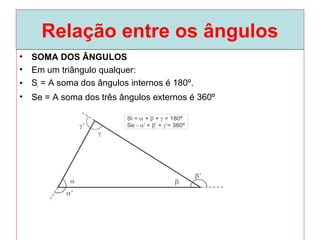
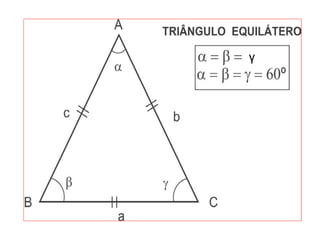
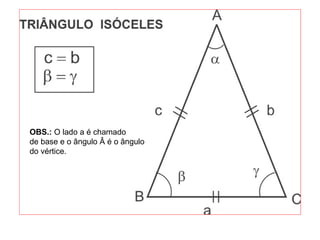
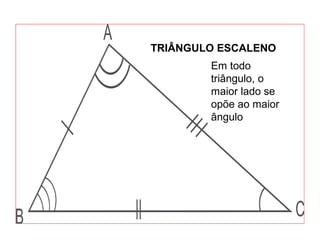
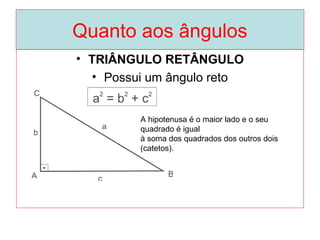
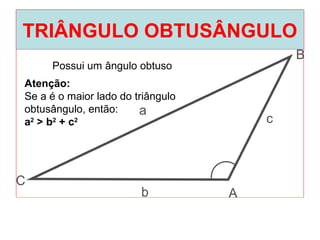
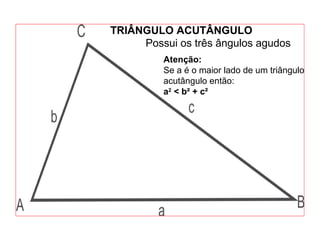
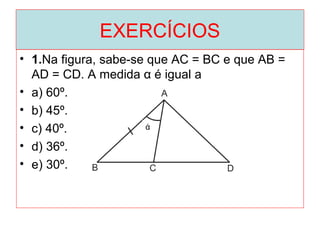
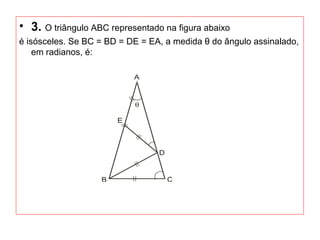
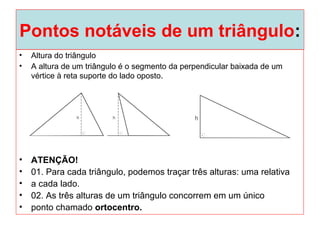
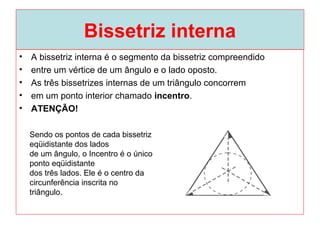
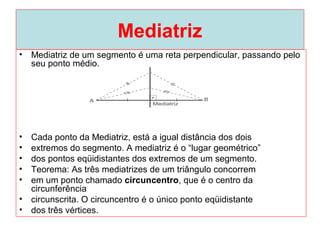
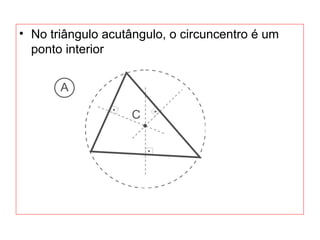
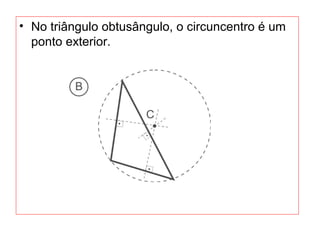
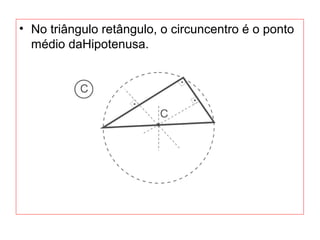
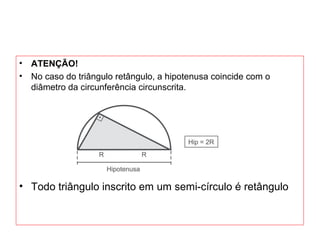
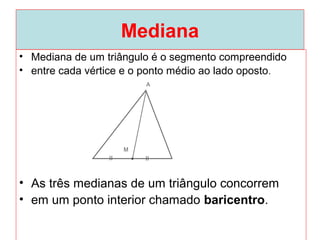
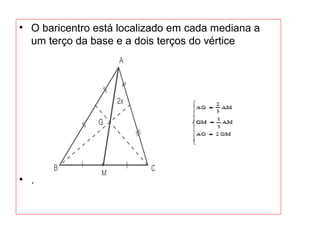
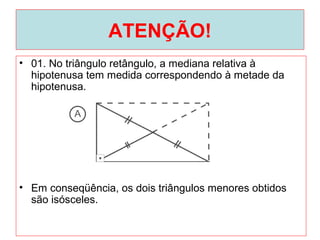
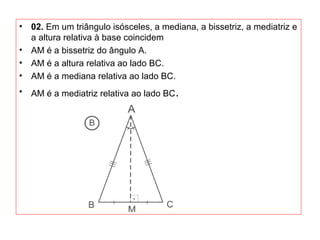
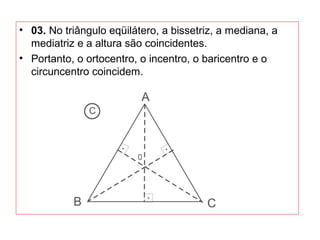
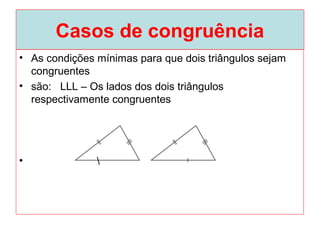
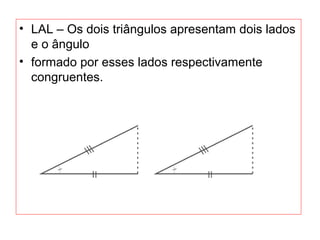
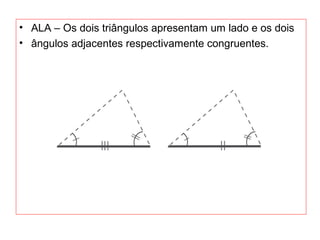
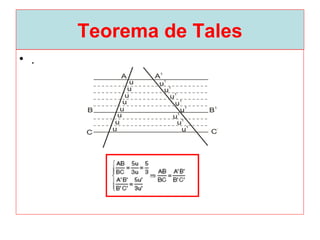
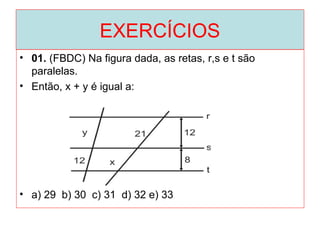
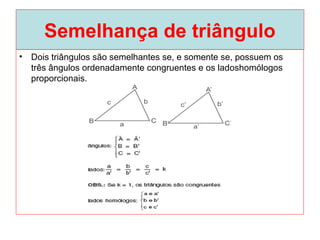
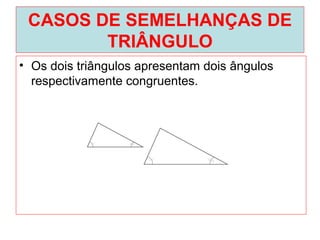
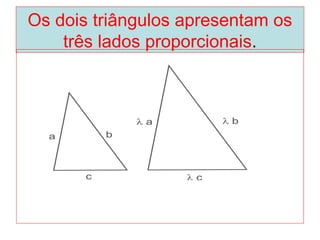
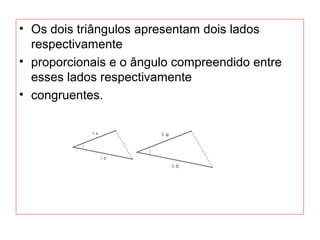
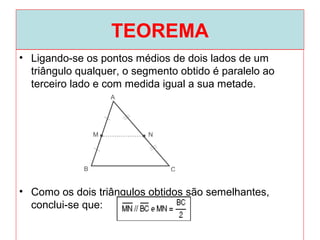
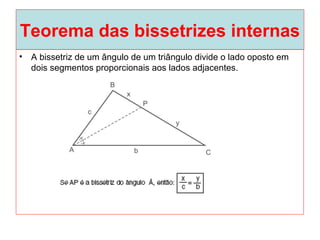
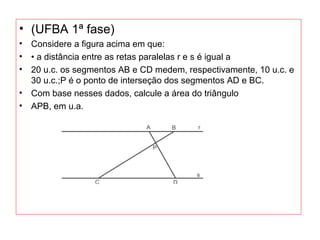
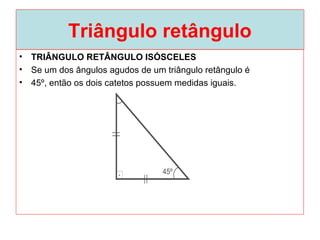
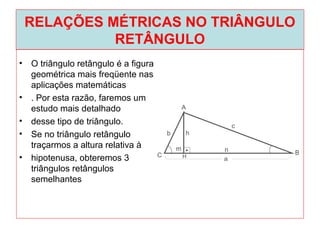
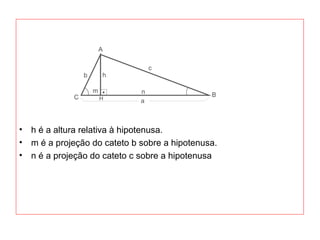
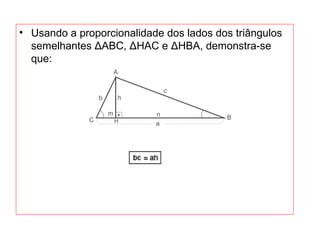
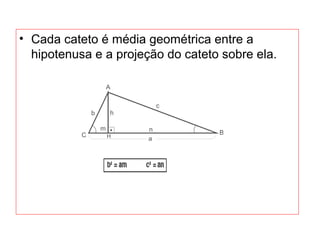
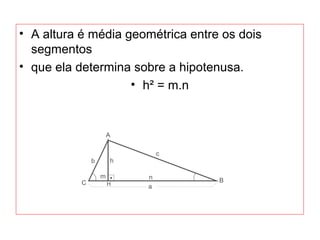
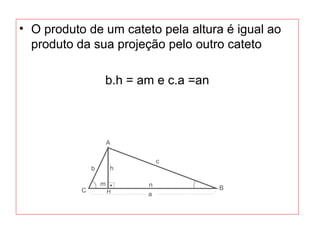
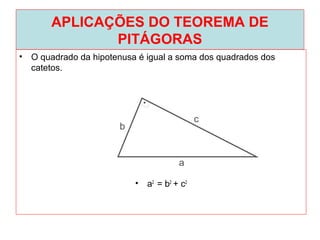
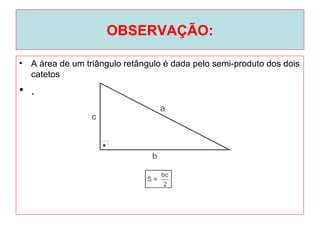
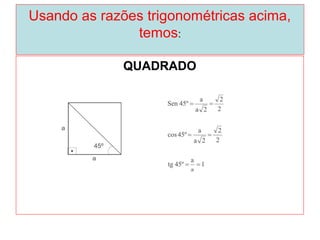
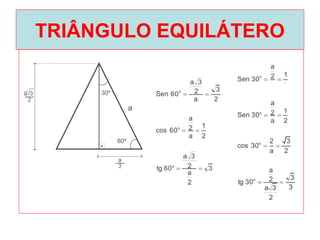
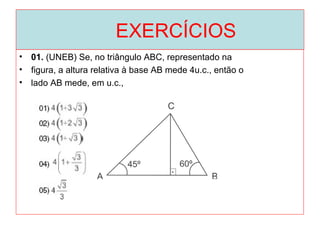
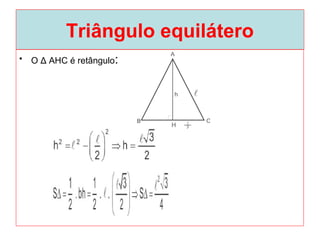
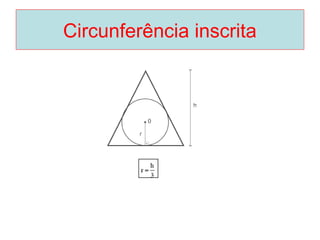
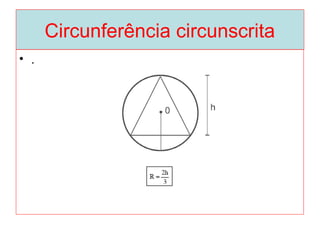
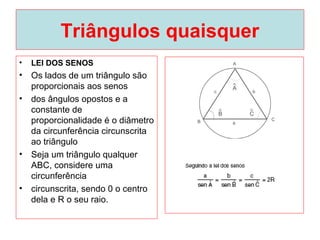
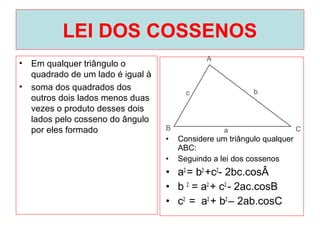
O documento introduz os conceitos básicos de geometria plana, incluindo: (1) os elementos primitivos de ponto, reta e plano; (2) as noções de figuras geométricas como triângulos e ângulos; (3) as propriedades e classificações de triângulos e ângulos.
Mais conteúdo relacionado
Geometria plana
- 1. GEOMETRIA PLANA Introdução Você vaiiniciar, agora, o estudo de uma das ciências mais belas criadas pelo homem: a Geometria. Nascida da necessidade de medir terras, encontra-se hoje presente, em todos os momentos do nosso dia-a-dia, nos tamanhos e formas dos objetos que nos cercam Na Geometria admitimos a existência de três elementos intuitivos, isto é, sem definição: ponto, reta e plano. A partir desses três elementos são construídas todas as demais figuras geométricas. A bem da verdade, esses três elementos existem apenas em nossa imaginação. Tentaremos criar algumas imagens concretas para representar o ponto, a reta e o plano, com a finalidade de ajudar um pouco nossa intuição Um pingo d’água, a cabeça de um alfinete, um grão de areia, a marca deixada por um lápis num papel são concretizações aproximadas da idéia de ponto; são aproximadas, pois o ponto geométrico não tem “tamanho”, isto é, não tem dimensão. Pense, agora, num barbante bem esticado: a figura obtida assemelha-se a um “pedaço” de reta; “pedaço”, pois a reta tem que ser entendida como infinitamente “comprida” em ambos os sentidos. Da mesma forma, você pode visualizar um plano imaginando uma folha de papel bem esticada:
- 2. NOÇÕES PRIMITIVAS • Asnoções primitivas são aceitas sem definição. • Adotaremos sem definir as noções de ponto, reta e plano. • PONTO • A . ou B . • Obs: As noções (conceitos, termos, entes) geométricos • são estabelecidas por meio de definição. RETA PLANO r
- 3. POSTULADOS OU AXIOMASOU PROPOSIÇÕES PRIMITIVAS • São proposições aceitas sem demonstração. EXEMPLO Por um ponto passam infinitas retas.
- 4. • POSTULADO DAEXISTÊNCIA • Numa reta, bem como fora dela, há infinitos pontos, A є r , B є r , C є r D r, E r, F r, G r∉ ∉ ∉ ∉
- 5. • Num plano, bem como fora dele, há infinitos pontos. A Є α, B Є α, C Є α D α, E α∉ ∉
- 6. • POSTULADO DADETERMINAÇÃO • Dois pontos distintos determinam uma única reta que passa • por eles. • r = AB obs .expressão duas retas coincidentes é equivalente a uma única reta.
- 7. • Três pontosnão colineares determinam um único plano que passa por eles. • α = (A, B, C)
- 8. POSTULADO DA INCLUSÃO •Se uma reta tem dois pontos distintos num plano, então areta está contida nesse mesmo plano.
- 9. É ESSENCIAL SABERQUE: • Pontos coplanares são pontos que pertencem a um • mesmo plano. • Pontos colineares são pontos que pertencem a uma • mesma reta. • Figura é qualquer conjunto de pontos. • Figura plana é uma figura que tem todos os seus pontos num mesmo plano. • Figura espacial é uma figura em que nem todos os • seus pontos estão em um mesmo plano. • Uma figura é convexa quando dois de seus pontos definem sempre um segmento inteiramente contido nela
- 10. Notações gráficas • Pontoscoplanares
- 11.
- 12.
- 13.
- 14.
- 15. Figura não convexa(côncava)
- 16. POSIÇÃO RELATIVA ENTRE DUASRETAS NO PLANO. • CONCORRENTES
- 17. PARALELAS Obs: A expressãoduas retas coincidentes é equivalente a uma única reta.
- 18. RETA,SEMI - RETAE SEGMENTO DE RETA • Considerando dois pontos distintos A e B, temos: • A reta AB • O segmento AB • A semi-reta AB • A semi-reta BA
- 19. SEGMENTOS CONSECUTIVOS • Doissegmentos de reta são consecutivos se, e somente • se, uma extremidade de um coincide com uma extremidade • do outro
- 20. SEGMENTOS COLINEARES • Doissegmentos de reta são colineares se, e somente se, • estão numa mesma reta. • AB e CD são colineares (não são consecutivos) • RS e ST são colineares (e consecutivos) MN e NP são colineares (e consecutivos)
- 21. SEGMENTOS ADJACENTES • Doissegmentos consecutivos e colineares são adjacentes se e somente se, possuem em comum apenas uma extremidade(não tem pontos internos comuns). • RS e ST não são adjacentes • RS ∩ ST = ST MN e NP são adjacentesMN ∩ NP = {N}
- 22. EXERCÍCIOS • 01. Assinaleas proposições verdadeiras: • (01) Por um ponto passam infinitas retas. • (02) Por três pontos dados passam uma só reta. • (04) Se dois pontos distintos de uma reta pertencem a • um plano, então a reta está contida nesse plano. • (08) Por dois pontos distintos passa uma reta. • (16) Três pontos distintos são sempre colineares. • (32) Duas retas distintas que têm um ponto comum são • concorrentes. • (64) Quatro pontos distintos são sempre coplanares.
- 23. • 02. DetermineAB, sendo M ponto médio de AB:
- 24. ÂNGULOS Definição A Ô B 0é o vértice do ângulo 0A e 0B são os lados Figura geométrica formada por duas semi-retas de mesma origem.
- 25. Bissetriz • Semi-reta quedivide o ângulo em dois ângulos congruentes. OM é a bissetriz
- 26. OBSERVAÇÕES: • 1) Adistância de um ponto P a uma reta r é dada pela medida do segmento da perpendicular que vai de P à reta r.
- 27. • 2) Cadaponto da bissetriz de um ângulo está a igual distância dos dois lados “A bissetriz é o lugar geométrico dos pontos eqüidistantes dos dois lados do ângulo”.
- 28. ÂNGULOS CONSECUTIVOS • Doisângulos são consecutivos quando têm o mesmo vértice e um lado comum. AÔB e BÔC AÔB e AÔC BÔC e AÔC
- 29. ÂNGULOS ADJACENTES • Doisângulos são adjacentes quando são consecutivos e não têm pontos internos comuns AÔB e BÔC
- 30. Medidas Angulares SISTEMA SEXAGESIMAL Oângulo reto se divide em 90º (noventa graus), cada grau em 60 (sessenta minutos) e cada minuto em 60’’ ’ (sessenta segundos). 1 reto = 90º 1º = 60’ 1’= 60’’.
- 31. SISTEMA CIRCULAR • Amedida de um ângulo central é dada em radiano pela razão entre o comprimento do arco e o raio. Na figura acima, o ângulo α, em radiano, é dado por
- 32. • Quando ocomprimento do arco é igual ao raio temos um radiano • . Tendo em vista que o comprimento da circunferência é C = 2πR, então a circunferência tem 2π rd. • Se 2π rd corresponde a 360o, então: • π rad corresponde a 180o • Os problemas da conversão de medidas de um sistema • para outro serão tratados em Trigonometria.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38. DUAS PARALELAS CORTADASPOR UMA TRANSVERSAL
- 39. Ângulos de ladosparalelos e ângulos de lados perpendiculares • São congruentes se ambos são agudos ou ambos obtusos. • São suplementares se um é agudo e o outro obtuso.
- 40. EXERCÍCIOS 1. Na figura, tem-sedois círculos concêntricos de raios 5 u. c. e 3 u.c., respectivamente. Sendo s1 o comprimento do arco AB e s2, o comprimento do arco A’B’, então o valor de s2 – s1, em unidade de comprimento, é aproximadamente igual a: 01) 0,52 02) 1,05 03) 1,57 04) 3,14 05) 4,71
- 41. • 2. Calculea medida do complemento e do suplemento do ângulo que mede: • a) 70º45’ • b) 85º50’’
- 42. • 03. Odobro do complemento de um ângulo,aumentado de 40º é igual a terça parte do suplemento do ângulo. Calcule o suplemento do ângulo.
- 43. • 4.Na figuraabaixo, as retas r e s são paralelas • A soma α + β é igual a: • a) 200º • b) 180º • c) 170 • d) 150º • e) 140º
- 44. TRIÂNGULO • Elementos dotriângulo • Vértices: A, B e C • Lados: AB, AC, e BC • Ângulos Internos: α, β e γ • Ângulos Externos: α’, β’, γ’
- 45. Relação entre asmedidas dos lados • Cada lado de um triângulo é maior do que o módulo da • diferença e menor do que a soma dos outros dois. • | b – c | < a < b + c • Ex.: Se 3 e 8 são as medidas de dois lados, o 3º lado é 5 < a < 11
- 46. Relação entre osângulos • SOMA DOS ÂNGULOS • Em um triângulo qualquer: • Si = A soma dos ângulos internos é 180º. • Se = A soma dos três ângulos externos é 360º
- 47. ÂNGULO EXTERNO • -Um ângulo externo e o interno consecutivos são • suplementares. α’+ α = 180º e α + β + γ = 180º→ α’= β + γ • Um ângulo externo vale a soma dos internos não adjacentes
- 48. Classificação dos triângulos •Quanto aos lados: • * Eqüilátero: três lados com medidas iguais. • * Isósceles: dois lados com medidas iguais (havendo um • lado diferente, ele é considerado a “base” do triângulo). • * Escaleno: não possui lados com medidas iguais. • OBS: Todo triângulo eqüilátero é também triângulo isósceles
- 49.
- 50. OBS.: O ladoa é chamado de base e o ângulo  é o ângulo do vértice.
- 51. TRIÂNGULO ESCALENO Em todo triângulo,o maior lado se opõe ao maior ângulo
- 52. Quanto aos ângulos •TRIÂNGULO RETÂNGULO • Possui um ângulo reto A hipotenusa é o maior lado e o seu quadrado é igual à soma dos quadrados dos outros dois (catetos).
- 53. TRIÂNGULO OBTUSÂNGULO Possui umângulo obtuso Atenção: Se a é o maior lado do triângulo obtusângulo, então: a2 > b2 + c2
- 54. TRIÂNGULO ACUTÂNGULO Possui ostrês ângulos agudos Atenção: Se a é o maior lado de um triângulo acutângulo então: a2 < b² + c²
- 55. EXERCÍCIOS • 1.Na figura,sabe-se que AC = BC e que AB = AD = CD. A medida α é igual a • a) 60º. • b) 45º. • c) 40º. • d) 36º. • e) 30º. ά
- 56. • 2. Combase no estudo dos triângulos, é correto • afirmar: a) Se o triângulo é isósceles, então é eqüilátero. b) É possível construir um triângulo com lados medindo 8u.c., 5u.c, e 18u.c. c) É possível construir um triângulo com ângulos medindo 30º , 40ºe 50º. d) Se um triângulo é retângulo e isósceles, então possui um ângulo de 45º. e) É possível construir um triângulo retângulo com lados medindo 1u.c., 1u.c. e 2u.c.
- 57. • 3. Otriângulo ABC representado na figura abaixo é isósceles. Se BC = BD = DE = EA, a medida θ do ângulo assinalado, em radianos, é:
- 58. Pontos notáveis deum triângulo: • Altura do triângulo • A altura de um triângulo é o segmento da perpendicular baixada de um vértice à reta suporte do lado oposto. • ATENÇÃO! • 01. Para cada triângulo, podemos traçar três alturas: uma relativa • a cada lado. • 02. As três alturas de um triângulo concorrem em um único • ponto chamado ortocentro.
- 59. Bissetriz interna • Abissetriz interna é o segmento da bissetriz compreendido • entre um vértice de um ângulo e o lado oposto. • As três bissetrizes internas de um triângulo concorrem • em um ponto interior chamado incentro. • ATENÇÃO! Sendo os pontos de cada bissetriz eqüidistante dos lados de um ângulo, o Incentro é o único ponto eqüidistante dos três lados. Ele é o centro da circunferência inscrita no triângulo.
- 60. Mediatriz • Mediatriz deum segmento é uma reta perpendicular, passando pelo seu ponto médio. • Cada ponto da Mediatriz, está a igual distância dos dois • extremos do segmento. A mediatriz é o “lugar geométrico” • dos pontos eqüidistantes dos extremos de um segmento. • Teorema: As três mediatrizes de um triângulo concorrem • em um ponto chamado circuncentro, que é o centro da circunferência • circunscrita. O circuncentro é o único ponto eqüidistante • dos três vértices.
- 61. • No triânguloacutângulo, o circuncentro é um ponto interior
- 62. • No triânguloobtusângulo, o circuncentro é um ponto exterior.
- 63. • No triânguloretângulo, o circuncentro é o ponto médio daHipotenusa.
- 64. • ATENÇÃO! • Nocaso do triângulo retângulo, a hipotenusa coincide com o diâmetro da circunferência circunscrita. • Todo triângulo inscrito em um semi-círculo é retângulo
- 65. Mediana • Mediana deum triângulo é o segmento compreendido • entre cada vértice e o ponto médio ao lado oposto. • As três medianas de um triângulo concorrem • em um ponto interior chamado baricentro.
- 66. • O baricentroestá localizado em cada mediana a um terço da base e a dois terços do vértice • .
- 67. ATENÇÃO! • 01. Notriângulo retângulo, a mediana relativa à hipotenusa tem medida correspondendo à metade da hipotenusa. • Em conseqüência, os dois triângulos menores obtidos são isósceles.
- 68. • 02. Emum triângulo isósceles, a mediana, a bissetriz, a mediatriz e a altura relativa à base coincidem • AM é a bissetriz do ângulo A. • AM é a altura relativa ao lado BC. • AM é a mediana relativa ao lado BC. • AM é a mediatriz relativa ao lado BC.
- 69. • 03. Notriângulo eqüilátero, a bissetriz, a mediana, a mediatriz e a altura são coincidentes. • Portanto, o ortocentro, o incentro, o baricentro e o circuncentro coincidem.
- 70. Casos de congruência •As condições mínimas para que dois triângulos sejam congruentes • são: LLL – Os lados dos dois triângulos respectivamente congruentes •
- 71. • LAL –Os dois triângulos apresentam dois lados e o ângulo • formado por esses lados respectivamente congruentes.
- 72. • ALA –Os dois triângulos apresentam um lado e os dois • ângulos adjacentes respectivamente congruentes.
- 73.
- 74. EXERCÍCIOS • 01. (FBDC)Na figura dada, as retas, r,s e t são paralelas. • Então, x + y é igual a: • a) 29 b) 30 c) 31 d) 32 e) 33
- 75. • 02. Notriângulo ABC, o lado AC mede 32 cm e o lado BC, 36cm. Por um ponto M situado sobre AC, a 10 cm dovértice C, traçamos a paralela ao lado AB, a qual divide BC em dois segmentos BN e CN. • Determine a medida de CN. • Matematica
- 76. Semelhança de triângulo •Dois triângulos são semelhantes se, e somente se, possuem os três ângulos ordenadamente congruentes e os ladoshomólogos proporcionais.
- 77. Teorema fundamental • Seuma reta é paralela a um dos lados de um triângulo e intercepta os outros dois em pontos distintos, então o triânguloque ela determina é semelhante ao primeiro
- 78. CASOS DE SEMELHANÇASDE TRIÂNGULO • Os dois triângulos apresentam dois ângulos respectivamente congruentes.
- 79. Os dois triângulosapresentam os três lados proporcionais.
- 80. • Os doistriângulos apresentam dois lados respectivamente • proporcionais e o ângulo compreendido entre esses lados respectivamente • congruentes.
- 81. TEOREMA • Ligando-se ospontos médios de dois lados de um triângulo qualquer, o segmento obtido é paralelo ao terceiro lado e com medida igual a sua metade. • Como os dois triângulos obtidos são semelhantes, conclui-se que:
- 82. Teorema das bissetrizesinternas • A bissetriz de um ângulo de um triângulo divide o lado oposto em dois segmentos proporcionais aos lados adjacentes.
- 83. EXERCÍCIOS • 01. (FJA/2006)Considerando-se as informações contidas na figura abaixo, pode-se concluir que o segmento CF mede:
- 84. • Na figura,está representada uma escada AB, de • comprimento c, apoiada em um muro. • Considerando-se essa informação, pode-se concluir que • o valor de c é igual, em metros
- 85. • (UFBA 1ªfase) • Considere a figura acima em que: • • a distância entre as retas paralelas r e s é igual a • 20 u.c. os segmentos AB e CD medem, respectivamente, 10 u.c. e 30 u.c.;P é o ponto de interseção dos segmentos AD e BC. • Com base nesses dados, calcule a área do triângulo • APB, em u.a.
- 86. Triângulo retângulo • TRIÂNGULORETÂNGULO ISÓSCELES • Se um dos ângulos agudos de um triângulo retângulo é • 45º, então os dois catetos possuem medidas iguais.
- 87. TRIÂNGULO RETÂNGULO COM ÂNGULODE 30º • A altura AH divide o triângulo equilátero ABC em dois triângulos retângulos que apresentam um ângulo de 30º. • Observando o triângulo AHC, concluímos: • Se o cateto se opõe a um ângulo de 30º, a sua medida é • igual a metade da hipotenusa.
- 88. RELAÇÕES MÉTRICAS NOTRIÂNGULO RETÂNGULO • O triângulo retângulo é a figura geométrica mais freqüente nas aplicações matemáticas • . Por esta razão, faremos um estudo mais detalhado • desse tipo de triângulo. • Se no triângulo retângulo traçarmos a altura relativa à • hipotenusa, obteremos 3 triângulos retângulos semelhantes
- 89. • h éa altura relativa à hipotenusa. • m é a projeção do cateto b sobre a hipotenusa. • n é a projeção do cateto c sobre a hipotenusa
- 90. • Usando aproporcionalidade dos lados dos triângulos semelhantes ΔABC, ΔHAC e ΔHBA, demonstra-se que:
- 91. • Cada catetoé média geométrica entre a hipotenusa e a projeção do cateto sobre ela.
- 92. • A alturaé média geométrica entre os dois segmentos • que ela determina sobre a hipotenusa. • h² = m.n
- 93. • O produtode um cateto pela altura é igual ao produto da sua projeção pelo outro cateto b.h = am e c.a =an
- 94. APLICAÇÕES DO TEOREMADE PITÁGORAS • O quadrado da hipotenusa é igual a soma dos quadrados dos catetos. • a2 = b2 + c2
- 95. OBSERVAÇÃO: • A áreade um triângulo retângulo é dada pelo semi-produto dos dois catetos • .
- 96. RAZÕES TRIGONOMÉTRICAS NO TRIÂNGULORETÂNGULO • Sendo α a medida de um dos ângulos agudos de um triângulo retângulo, temos:
- 97. Usando as razõestrigonométricas acima, temos: QUADRADO
- 98.
- 99. EXERCÍCIOS • 01. (UNEB)Se, no triângulo ABC, representado na • figura, a altura relativa à base AB mede 4u.c., então o • lado AB mede, em u.c.,
- 100. • 02. (FRB)Um observador, ao nível do chão, avista a • base da janela J1 segundo um ângulo α = 30º e a J2, • segundo um ângulo β = 45º, como mostra a figura. • Sendo a distância entre as bases das duas janelas igual • a 3m, pode-se afirmar que a distância h, do chão à base • de J1, mede, em metros,
- 101. Triângulo equilátero • OΔ AHC é retângulo:
- 102.
- 103.
- 104. Triângulos quaisquer • LEIDOS SENOS • Os lados de um triângulo são proporcionais aos senos • dos ângulos opostos e a constante de proporcionalidade é o diâmetro da circunferência circunscrita ao triângulo • Seja um triângulo qualquer ABC, considere uma circunferência • circunscrita, sendo 0 o centro dela e R o seu raio.
- 105. LEI DOS COSSENOS •Em qualquer triângulo o quadrado de um lado é igual à • soma dos quadrados dos outros dois lados menos duas vezes o produto desses dois lados pelo cosseno do ângulo por eles formado • Considere um triângulo qualquer ABC: • Seguindo a lei dos cossenos • a2 = b2 +c2 - 2bc.cos • b 2 = a2 + c2 - 2ac.cosB • c2 = a2 + b2 – 2ab.cosC
Notas do Editor
- #4 EXEMPLO Por um ponto passam infinitas retas.
- #25 DefiniçãoFigura geométrica formada por duas semi-retas de mesma origem. 0 é o vértice do ângulo 0A e 0B são os lados
- #26 OM é a bissetriz
- #32 Na figura acima, o ângulo α, em radiano, é dado por
- #48 - Um ângulo externo e o interno consecutivos são suplementares. α’+ α = 180o
- #53 A hipotenusa é o maior lado e o seu quadrado é igual à soma dos quadrados dos outros dois (catetos).