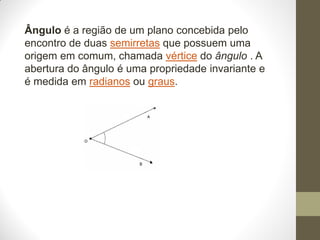
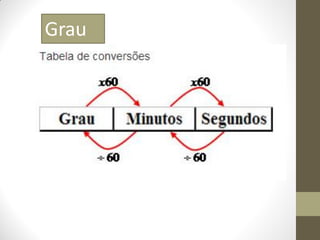
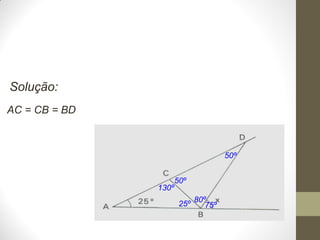
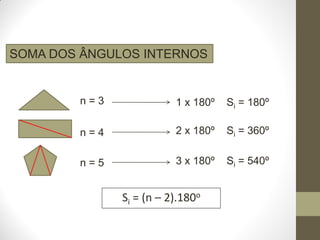
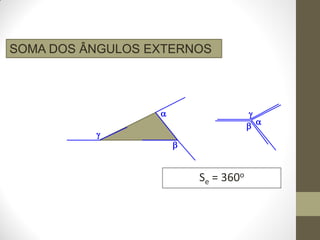
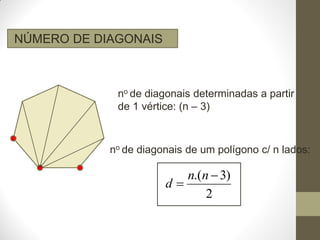
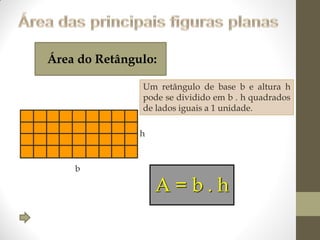
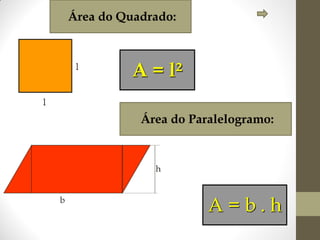
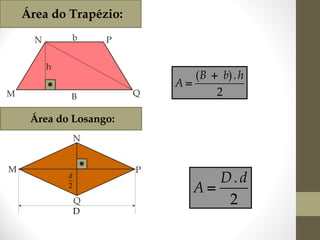
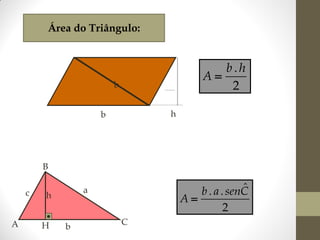
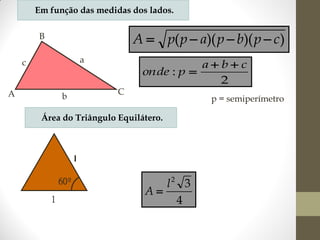
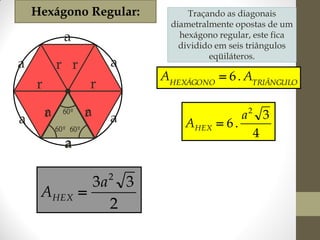
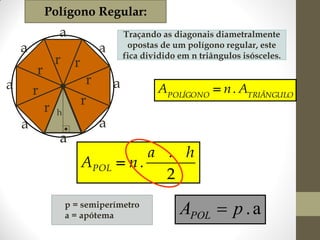
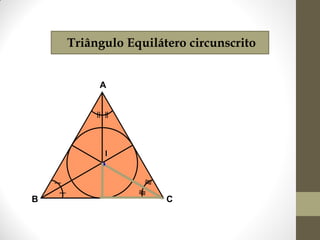
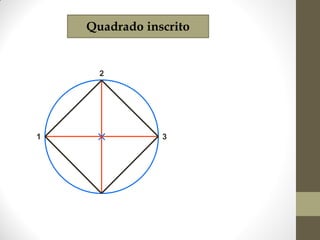
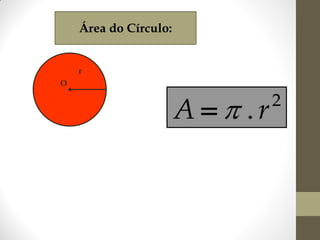
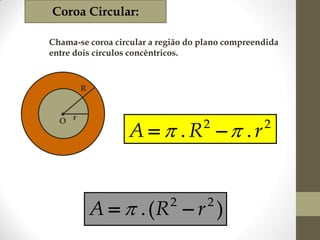
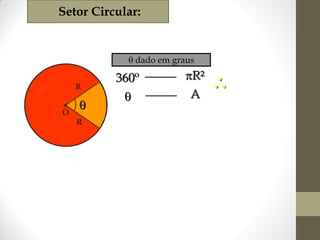
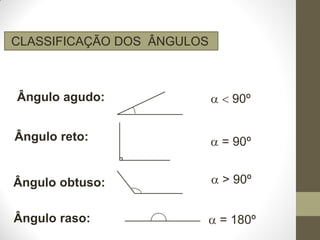
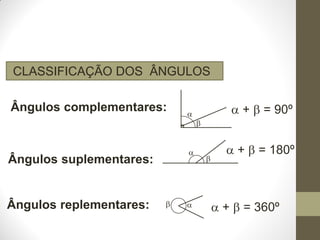
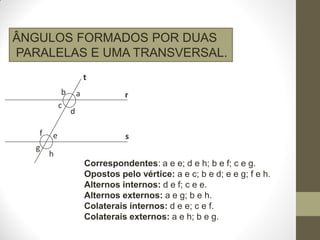
1) O documento discute ângulos, suas classificações e propriedades. É apresentada a definição de ângulo e as unidades de medida. 2) São listados os diferentes tipos de ângulos como agudo, reto e obtuso. 3) São explicados conceitos como ângulos adjacentes, complementares e suplementares.

1. PROFESSORA ROSANA QUIRINO

2. Ângulo é a região de um plano concebida pelo
encontro de duas semirretas que possuem uma
origem em comum, chamada vértice do ângulo . A
abertura do ângulo é uma propriedade invariante e
é medida em radianos ou graus.

3. Grau

4. Radiano
0
𝜋𝑟𝑎𝑑 = 180
0
1𝑟𝑎𝑑 ≅ 57

5. CLASSIFICAÇÃO DOS ÂNGULOS
Ângulo agudo:
  90º
Ângulo reto:
 = 90º
Ângulo obtuso:
 > 90º
Ângulo raso:
 = 180º

6. Ângulo nulo:
(lados coincidentes)
Ângulo de 1 volta:
Ângulos adjacentes:
Ângulos consecutivos:
 = 0o
 = 360o

7. CLASSIFICAÇÃO DOS ÂNGULOS
Ângulos complementares:

Ângulos suplementares:
Ângulos replementares:



 +  = 90º


 +  = 180º
 +  = 360º

8. ÂNGULOS FORMADOS POR DUAS
PARALELAS E UMA TRANSVERSAL.
t
b
c
f
g
e
a
r
d
s
h
Correspondentes: a e e; d e h; b e f; c e g.
Opostos pelo vértice: a e c; b e d; e e g; f e h.
Alternos internos: d e f; c e e.
Alternos externos: a e g; b e h.
Colaterais internos: d e e; c e f.
Colaterais externos: a e h; b e g.

9. (UFES) O triplo do complemento de um ângulo é igual à
terça parte do suplemento deste ângulo. Este ângulo mede:
a) 45o
b) 48o 30’
c) 56o 15’
d) 60o
e) 78o 45’
1
3.(90  x)  .(180  x)
3
1
270  3 x  .(180  x)
3
810  9 x  180  x
8 x  630
x  78o 45'

10. Se as retas r e s da figura abaixo são paralelas então 3 + 
vale:
a) 225o
b) 195o
c) 215o
d) 1750
e) 1850

11. Solução:
= 45º
 = 60º
15º
30º
3    3.45  60
3    195o
30º
60º
60º

12. Na figura, AC = CB = BD e A = 25o. O ângulo x mede:
a) 50o
b) 60o
c) 70o
d) 75o
e) 80o

13. Solução:
AC = CB = BD
50º
130º
50º
25º
80º
75º

14. POLÍGONOS CONVEXOS E NÃO-CONVEXOS
CONVEXO
NÃO-CONVEXO

15. SOMA DOS ÂNGULOS INTERNOS
n=3
1 x 180º
Si = 180º
n=4
2 x 180º
Si = 360º
n=5
3 x 180º
Si = 540º
Si = (n – 2).180o

16. SOMA DOS ÂNGULOS EXTERNOS



 

Se = 360o

17. NÚMERO DE DIAGONAIS
no de diagonais determinadas a partir
de 1 vértice: (n – 3)
no de diagonais de um polígono c/ n lados:
n.(n  3)
d
2

18. Áreas de
Figuras Planas

19. Área do Retângulo:
Um retângulo de base b e altura h
pode se dividido em b . h quadrados
de lados iguais a 1 unidade.
h
b
A=b.h

20. Área do Quadrado:
l
A = l²
l
Área do Paralelogramo:
h
b
A=b.h

21. Área do Trapézio:
b
N
P
h
M
B
Q
( B  b) . h
A
2
Área do Losango:
N
M
d
2
P
d
2
Q
D
D. d
A
2

22. Área do Triângulo:
b.h
A
2
b
h
b
B
c
A
h
H
ˆ
b . a . senC
A
2
a
b
C

23. Em função das medidas dos lados.
A  p( p  a)( p  b)( p  c )
B
a
c
A
C
b
abc
onde : p 
2
p = semiperímetro
Área do Triângulo Equilátero.
l
60º
l
l2 3
A
4

24. Hexágono Regular:
a
a
a
r r
a
AHEXÁGONO  6 . ATRIÂNGULO
r
r
a
r
60º
a
r
a
60º 60º
AHEX
a
AHEX 
3a
2
2
Traçando as diagonais
diametralmente opostas de um
hexágono regular, este fica
dividido em seis triângulos
eqüiláteros.
3
a2 3
 6.
4

25. Polígono Regular:
a
a
a
a
a
r r
r
r
r
h
r
a
Traçando as diagonais diametralmente
opostas de um polígono regular, este
fica dividido em n triângulos isósceles.
r
r
a
APOLÍGONO  n . ATRIÂNGULO
a
APOL
a . h
 n.
2
p = semiperímetro
a = apótema
APOL  p . a

26. Triângulo Equilátero circunscrito
A
.
I
B
C

27. Quadrado inscrito
2
1
3

28. Área do Círculo:
r
O
A   .r
2

29. Coroa Circular:
Chama-se coroa circular a região do plano compreendida
entre dois círculos concêntricos.
R
O r
A   . R  .r
2
A   . (R  r )
2
2
2

30. Setor Circular:
 dado em graus
R
O

R
360º

R²
A


31. Segmento Circular:
 < 180º
A
R
O
A = ASETOR - ATRIÂNGULO

R
B
 > 180º
A = ASETOR + ATRIÂNGULO