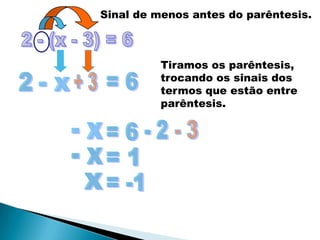
Este documento fornece instruções sobre expressões e equações algébricas em 3 passos: (1) explica como adicionar termos semelhantes em expressões algébricas; (2) define equações e suas soluções; (3) lista etapas para resolver equações com parênteses e denominadores.

1. Ano Letivo 2011/2012
Lorena Monteiro, 8º1

2.  Uma expressão algébrica é  Exemplo: 3x – 5a – 3 + 8a - 10x
uma expressão matemática
que normalmente contém uma  3x; –5a; –3; 8a e -10x são os
ou mais letras termos da expressão algébrica.
 No termo 3x, 3 é o coeficiente e
 Dois termos de uma x é a parte literal.
expressão algébrica  Os termos 3x e -10x têm a
dizem-se semelhantes se mesma parte literal, assim como
os termos -5a e 8a.
tiverem a mesma parte
literal.  ASSIM:
3x-10x = (3-10)x=-7x e
 Para adicionar termos
-5a+8a=(-5+8)a=3a .
semelhantes, adicionam-se os
coeficientes mantêm-se a
LOGO: 3x-5a-3+8a-10x = -7x+3a-3.
parte literal.

3. -0,5x - (5x-4) = -0,5x - 5x + 4 = -5,5x + 4 .
-2(x - y)= -2x + 2y.
3x - 3(-y + 2) + (3x - y) = 3x + 3y – 6 + 3x – y = 6x + 2y - 6

4.  Uma equação é uma igualdade onde podem figurar letras
designadas por incógnitas.
 Solução de uma equação com uma incógnita é um número que
quando colocado no lugar da incógnita a transforma numa
igualdade numérica verdadeira.
 Equações Equivalentes são equações que têm o mesmo conjunto-
solução.

5.  Equações com parênteses
Usamos a propriedade distributiva da multiplicação em relação à adição
nas equações com parênteses.
-2(x+3) = 4  -2x-6=4
 Princípio de equivalência da adição
Se adicionarmos (subtrairmos) a mesma quantidade a ambos os membros
de uma equação obtemos uma equação equivalente.
Regra da Adição
numa equação, podemos mudar um termo de um membro para o outro se
lhe trocarmos o sinal.
x+6 = 4  x+6-6 = 4-6  x=-2
 Princípio de equivalência da multiplicação
Se multiplicarmos (dividirmos) ambos os membros de uma equação pelo
mesmo número, diferente de zero, obtemos uma equação equivalente.
-3x = 6  -3x/-3 = 6/-3  x = -2

6. Desembaraçar de
parêntesis, aplicando a
propriedade distributiva da
multiplicação.

7. Sinal de menos antes do parêntesis.
Tiramos os parêntesis,
trocando os sinais dos
termos que estão entre
parêntesis.

8. Equações com Denominadores
2x 1 x 2
•Identificar qual vai ser o
3 2 3 denominador comum a
todos os termos
2x 1 x 2
3 ( 2) 2 ( 3) 3 ( 2) •Reduzimos todos os
termos ao mesmo
denominador.
4x 3 2x 4
6 6 6 •Eliminar os
denominadores
4x 3 2x 4
4x 3 2x 4
4x 2x 4 3
2x 7
7
x
2

9.  1º- Desenvolver os parênteses de acordo com as
operações em causa.
 2º- Determinar o m.m.c dos números que estão no
denominador.
 3º- Simplificar as expressões nos dois membros da
equação.
 4º- Resolver a equação sem parênteses e sem
denominadores aplicando os princípios anteriores.