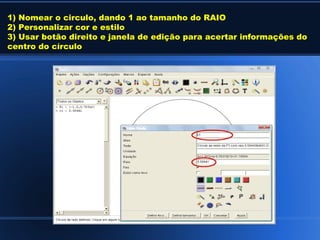
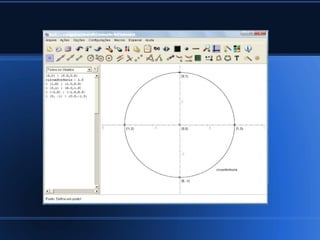
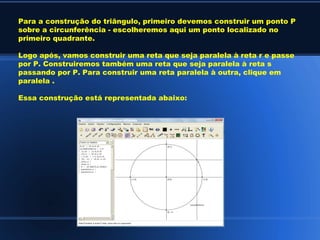
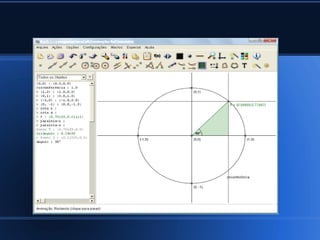
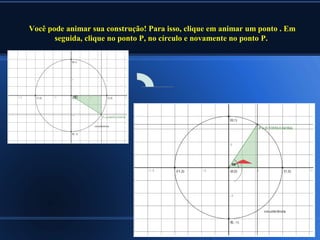
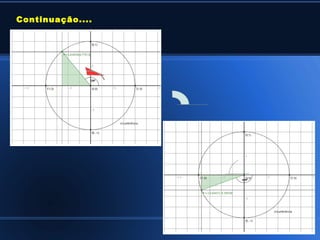
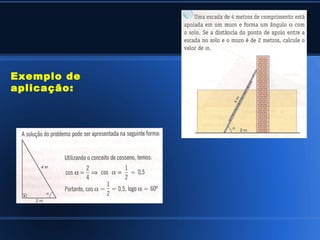
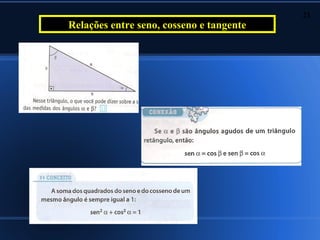
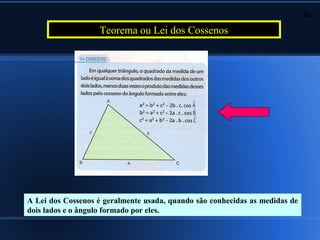
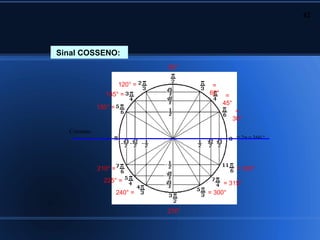
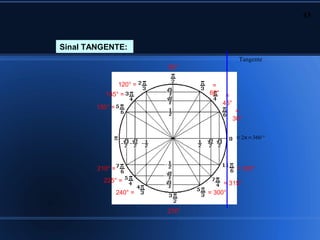
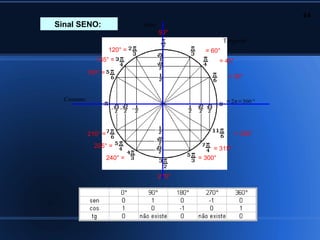
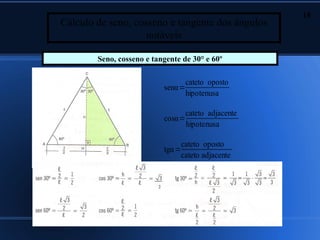
O documento discute conceitos básicos de trigonometria, incluindo: 1) A definição de trigonometria e seu significado; 2) Aplicações da trigonometria em triângulos retângulos e a relação entre seno, cosseno e tangente; 3) Cálculo de seno, cosseno e tangente de ângulos notáveis.

1. 26/10/2012

2. 2
Trigonometria
O significado da palavra trigonometria, vem do
grego e resulta da conjunção de três palavras:
Tri – três
Gonos – ângulo
Metrein - medir
Trigonometria significa, o estudo das medidas
dos triângulos.

3. 3

4. 4
Aplicações da Trigonometria

5. 5

6. 7
Triângulo retângulo
Triângulo retângulo é todo triângulo que apresenta um
ângulo reto, ou seja, um ângulo de 90°.
cateto hipotenu
cateto
cateto sa
cateto
hipotenu
sa
A hipotenusa é sempre o maior lado do triângulo retângulo;
Em qualquer triângulo, a soma dos ângulos internos é sempre 180°;
Como num triângulo retângulo um dos ângulos é reto, a soma dos outros
dois ângulos agudos (menores que 90º) é sempre 90°;
Quando a soma de dois ângulos internos é igual a 90°, dizemos que esses
ângulos são complementares.

7. 8
Teorema de Pitágoras
Em todo triângulo retângulo, o quadrado da medida da hipotenusa é
igual a soma dos quadrados das medidas dos catetos.
a=5
b=3 a 2 =b 2 +c 2
52 =3 2+ 4 2
25=9+ 16
25=25
c=4

8. 12
Relações Trigonométricas num triângulo retângulo
Seno Cosseno
Tangente

9. 13
Exemplo de aplicação:

10. 15
Exemplo de
aplicação:

11. 17
Exemplo de aplicação:

12. 18
Cálculo de seno, cosseno e tangente dos ângulos
notáveis
Seno, cosseno e tangente de 30° e 60º
cateto oposto
senα=
hipotenusa
cateto adjacente
cosα=
hipotenusa
cateto oposto
tgα =
cateto adjacente
2

13. 19
Seno, cosseno e tangente de 45°
cateto oposto
senα=
hipotenusa
cateto adjacente
cosα=
hipotenusa
cateto oposto
tgα=
cateto adjacente

14. 20
Construção da Tabela
Trigonométrica

15. 21
Relações entre seno, cosseno e tangente

16. 22

17. 23
Observe a situação a seguir:
Um fio elétrico será instalado entre um poste P e uma casa, separados
por um lago em um terreno plano. Como calcular o comprimento do
fio necessário para a instalação?
Pela necessidade de solucionar
problemas relacionados a triângulos
que não são retângulos, se
desenvolveram formas de trabalhar
com senos e cossenos de ângulos
obtusos ( maiores que 90°).

18. 24
Teorema ou Lei dos Senos
A lei dos senos pode ser utilizada em
qualquer triângulo. No caso de
triângulos retângulos, basta considerar
sen 90° = 1.

19. 25
Aplicação da Lei dos Senos
A Lei dos Senos é geralmente usada, quando são conhecidos 2 ângulos internos
e a medida do cateto oposto a um desses ângulos.

20. 26
Teorema ou Lei dos Cossenos
A Lei dos Cossenos é geralmente usada, quando são conhecidas as medidas de
dois lados e o ângulo formado por eles.

21. 27
Exemplo:

22. 28
Área de um triângulo

23. 29
Existem problemas em que se deseja calcular a área de um triângulo
e não são conhecidas as medidas da base e altura. Nesses casos,
a área pode ser calculada de duas maneiras diferentes:
1ª maneira: Área de um triângulo em função da medidas de
dois lados e do ângulo compreendido entre eles.

24. 30
2ª maneira: Fórmula de Heron

25. 31

26. 38
CIRCUNFERÊNCIA TRIGONOMÉTRICA

27. CIRCUNFERÊNCIA TRIGONOMÉTRICA:
Arcos Simétricos
π
90°=
2
IIQ :180 ° −α IQ : α
π−α
180°= π
360°=2π
IIIQ :180°+ α
IV :360 °−α
π+α
2 π-α
3π
270°=
2

28. 42
Sinal COSSENO:
90°
120° = =
135° = 60° =
45°
150° =
=
30°
Cosseno
=2π=360 °
210° = = 330°
225° = = 315°
240° = = 300°
270°

29. 43
Sinal TANGENTE:
Tangente
90°
120° = =
135° = 60° =
45°
150° =
=
30°
=2π=360 °
210° = = 330°
225° = = 315°
240° = = 300°
270°

30. 44
Sinal SENO: Seno
90°
Tangente
120° = = 60°
135° = = 45°
150° =
= 30°
Cosseno =2π=360 °
210° = = 330°
225° = = 315°
240° = = 300°
270°

31. 45
OUTRAS RAZÕES TRIGONOMÉTRICAS
1
Secante: o sinal da secante é o mesmo do cosseno sec x=
cos x
Cossecante: o sinal da cossecante é o mesmo do
1
cossec x=
seno sen x
Cotangente: o sinal da cotangente é o mesmo da
cos x
cot gx=
tangente. sen x

32. Para iniciar desenhando a circunferência clique em
"círculo de raio fixo", como mostra a figura abaixo.

33. 1) Nomear o circulo, dando 1 ao tamanho do RAIO
2) Personalizar cor e estilo
3) Usar botão direito e janela de edição para acertar informações do
centro do círculo

34. Por uma questão de conveniência, o centro de nossa circunferência será
a origem. Para determinar o centro como o ponto (0,0) basta alterar os
valores de x e y para 0, na janela de edição desse ponto.
Para uma visualização com os eixos coordenados basta clicar na opção
exibir grade ,no menu de comandos do software.
Localizaremos tambémos pontos (1,0), (0,1), (-1,0) e (0,-1). Para localizá-
los, clique na opção ponto , no menu de comandos. Para editá-los, basta
clicar com o botão direito do mouse e digitar a coordenada do ponto em
"nome".
Caso o nome do ponto - ou de qualquer outro objeto - não esteja
aparecendo, clique em exibir nomes dos objetos , na janela de edição do
próprio objeto.
Veja figura a seguir:

36. Desenharemos agora retas que "passam em cima" dos eixos
coordenados (essa construção será feita para auxiliar futuramente
na construção do triângulo, onde estudaremos as funções seno e
cosseno).
Assim, para construir essas retas basta clicar em reta . Clique no
ponto (-1, 0) e logo após em (1, 0) para construir a reta r que "passa
em cima" do eixo das abscissas - ou primeiro em (1, 0) e depois em (-
1, 0).
Para construir a reta s, que "passa em cima" do eixo das ordenadas,
basta selecionar a opção perpendicular . Clique então sobre a reta
construída anteriormente e logo após clique no ponto (0, 1) - ou no
ponto (0, -1). (Poderíamos também construir essa segunda reta da
mesma maneira como construímos a primeira)
Obs: Para visualizar se as retas foram de fato construídas, selecione
exibir grade duas vezes, para que os eixos coordenados sejam
ocultos.
Veja figura a seguir:

38. Para a construção do triângulo, primeiro devemos construir um ponto P
sobre a circunferência - escolheremos aqui um ponto localizado no
primeiro quadrante.
Logo após, vamos construir uma reta que seja paralela à reta r e passe
por P. Construiremos também uma reta que seja paralela à reta s
passando por P. Para construir uma reta paralela à outra, clique em
paralela .
Essa construção está representada abaixo:

39. Para a construção do triângulo, selecione a opção polígono . Clique na
origem, no ponto P, na interseção das retas s e paralela-s e finalize o
triângulo clicando novamente na origem.
Você pode editar o triângulo clicando com o botão direito do mouse
sobre ele.
Você pode também determinar o ângulo compreendido entre P, a
origem e o eixo das abscissas. Para tanto, basta, primeiramente,
desenhar um ponto Q sobre o eixo x perto da origem. Clique em ângulo
e selecione esses três vértices que irão compreender esse ângulo.
Você pode editar também o ângulo, selecionando nele com o botão
direito do mouse sobre ele. Para permitir uma visão do ângulo menos
"poluída", você pode ocultar esse ponto Q, editando-o.

41. Você pode animar sua construção! Para isso, clique em animar um ponto . Em
seguida, clique no ponto P, no círculo e novamente no ponto P.

42. Continuação....

43. EXEMPLO DE APLICAÇÃO
I) Seno e Cosseno de um arco
1. Utilizando a opção mover ponto no menu de comandos,
você pode mover o ponto P e observar o que ocorre com
suas coordenadas.
a) Mova o ponto P até que o ângulo formado seja de 45º (o
ângulo é formado por P, origem e eixo das abscissas).
Tente estimar o valor do seno deste ângulo, através das
relações no triângulo retângulo (lembre-se de que o raio da
circunferência mede 1). Tente estimar também o valor do
cosseno de 45º.
b) De modo semelhante, estime o valor do seno e do
cosseno de 30º.
2. Quando consideramos uma circunferência de raio igual a
1, a que conclusão podemos chegar sobre as coordenadas
do ponto P, ou seja, qual o significado da coordenada x do
ponto P? Qual o significado da coordenada y desse ponto?

44. EXEMPLO DE APLICAÇÃO...
3. Considere agora o primeiro quadrante (ângulos entre 0 e 90º) do
círculo. Os valores para o seno de um arco (arco é o "pedacinho"
da circunferência de extremos (1,0) e P, como se fosse a borda de
uma fatia de pizza) nesse quadrante são positivos ou negativos?
Quanto aos valores do cosseno, são positivos ou negativos?
4. Considere agora o segundo quadrante (ângulos entre 90º e 180º).
Observe que os quadrantes do círculo trigonométrico são
deteminados no sentido anti-horário. Os valores para o seno de um
arco nesse quadrante são positivos ou negativos? Quanto aos
valores do cosseno, são positivos ou negativos?
5. Considere agora o terceiro quadrante (ângulos entre 180º e
270º). Os valores para o seno de um arco nesse quadrante são
positivos ou negativos? Quanto aos valores do cosseno, são
positivos ou negativos?

45. EXEMPLO DE APLICAÇÃO...
6. Considere agora o quarto quadrante (ângulos entre 270º e
360º). Os valores para o seno de um arco nesse quadrante são
positivos ou negativos? Quanto aos valores do cosseno, são
positivos ou negativos?
7. Para determinar o sinal do seno de um arco, basta olharmos
até que quadrante um arco está desenhado. O valor do seno de
um arco é medido através de qual eixo coordenado? Em quais
quadrantes o valor do seno será positivo? Onde ele será
negativo? Por quê?
8. Para determinar o sinal do cosseno de um arco, basta olharmos
até que quadrante um arco está desenhado. O valor do cosseno
de um arco é medido através de qual eixo coordenado? Em quais
quadrantes o valor do cosseno será positivo? Onde ele será
negativo? Por quê?

46. EXEMPLO DE APLICAÇÃO...
9. Utilizando a construção feita no Régua e Compasso,
determine o valor máximo do seno de um arco. Detemine
também o valor mínimo. Com relação ao cosseno, qual seu
valor máximo e mínimo?
10. Determine o seno e o cosseno dos seguintes ângulos:
a) 0º b) 90º c) 180º d) 270º e) 360º
11. Disponha em ordem crescente o seno e o cosseno dos
seguintes ângulos: 20º, 170º, 260º, 300º.
12. Disponha em ordem crescente os seguintes números reais:
a) sen 50º, sen 100º, sen 200º, sen 300º
b) cos 50º, cos 100º, cos 200º, cos 300º

47. REDUÇÃO AO PRIMEIRO QUADRANTE
Podemos obter valores de senos e cossenos de arcos dos 2º, 3º e 4º
quadrantes, usando os valores do 1º quadrante. Assim, observe as
figuras abaixo e determine:
a) os ângulos que estão faltando (aqueles que possuem um ponto de
interrogação)
b) o valor do seno e do cosseno dos quatro ângulos de cada figura

48. Considerações Finais
Este trabalho não foi montado com ideias exclusivamente
minhas. Fiz diversas pesquisas na INTERNET buscando
situações semelhantes àquelas que tinham relação com o meu
planejamento original.
Este trabalho não é uma cópia, mas estão aqui presentes
diversos elementos idênticos aos utilizados pelos seus
criadores.
Uma vez disponível na REDE, o material encontrado está
destinado ao aprendizado do conteúdo.
Numa eventual aula, com recursos digitais, não está
descartada a hipótese de substituir este trabalho pelo acesso
direto a alguns links citados nas referências.
JULIO CESAR FACINA NETTO

49. Referências
http://pt.wikipedia.org/wiki/Projeto_de_aprendizagem
http://programaamigodevalor.ning.com/?
utm_source=google&utm_medium=cpc&utm_term=educacao&utm_campaign=amigo_valor
http://www2.mat.ufrgs.br/~mat01074/20072/grupos/quefren_queops/lista_rec.htm
http://stg2.novoser.com.br/SER_PP'%20CDConvSim/000895/trigonometria4.swf
http://www2.mat.ufrgs.br/~mat01074/20072/grupos/quefren_queops/tutorial_rec.htm
http://www.serprofessoruniversitario.pro.br/m%C3%B3dulos/metodologia-da-
pesquisa/instrumentos-de-coleta-de-dados-em-pesquisas-educacionais#.UHm5N2-jatZ
http://www.google.com.br/url?
sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0CCEQFjAA&url=http%3A%2F
%2Fwww.pmerechim.rs.gov.br%2Fuploads%2Ffiles%2FRevis%25C3%25A3