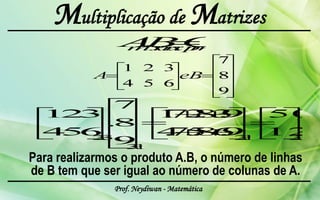
O documento apresenta os principais conceitos e notações relacionados a matrizes, incluindo: definição de matriz, tipos de matrizes (linha, coluna, quadrada, diagonal, identidade, transposta), igualdade e operações entre matrizes (adição, subtração, multiplicação por número e entre matrizes), propriedades de matrizes e inversão de matrizes.

2. Definição e Notação
a11
a21
Chamamos de Matriz a todo conjunto de “valores”, .
dispostos em linhas e colunas. Representamos .
matrizes com letras maiúsculas do nosso alfabeto. .
Prof. Neydiwan - Matemática am1

3. Matriz Linha
A 4 2 1 0
É toda matriz que possui apenas uma linha.
Prof. Neydiwan - Matemática

4. Matriz Coluna
5
B 4
10
É toda matriz que possui apenas uma coluna.
Prof. Neydiwan - Matemática

5. Matriz Quadrada
1 2 0
C 5 2 6
5 0 2
É toda matriz onde o número de linhas é igual
ao número de colunas.
Prof. Neydiwan - Matemática

6. Matriz Diagonal
5 0 0
D 0 4 0
0 0 1
É toda matriz quadrada onde os termos que não
estão na diagonal principal são nulos.
Prof. Neydiwan - Matemática

7. Matriz Identidade
1 0 0
D 0 1 0
0 0 1
É toda matriz quadrada onde os termos que estão na
diagonal principal são iguais a 1 e os outros são
nulos.
Prof. Neydiwan - Matemática

8. Matriz Transposta
É toda matriz onde os termos que estão na posição
de linha são transpostos para a posição de coluna.
Prof. Neydiwan - Matemática

9. Igualdade de Matrizes
Duas matrizes são iguais quando todos os elementos
correspondentes são iguais.
Prof. Neydiwan - Matemática

10. Adição e Subtração de Matrizes
Para realizarmos estas operações entre matrizes,
precisamos ter matrizes de mesma ordem e realizar
as respectivas operações com os elementos
correspondentes.
Prof. Neydiwan - Matemática

11. Multiplicação de Matriz Por Um Número
Para realizarmos o produto de uma constante por
uma matriz, basta multiplicarmos todos os elementos
pela constante dada.
Prof. Neydiwan - Matemática

12. Multiplicação de Matrizes
Para realizarmos o produto A.B, o número de linhas
de B tem que ser igual ao número de colunas de A.
Prof. Neydiwan - Matemática

13. Propriedades de Matrizes
1 A B C A B C
2 A B B A
3 A M A
4 A A' 0
Prof. Neydiwan - Matemática

14. Propriedades de Matrizes
1 a. b. A a.b . A
2 a. A B a. A a.B
3 a b . A a. A b. A
4 1. A A
Prof. Neydiwan - Matemática

15. Propriedades de Matrizes
1 A.B .C A B.C
2 A B .C C. A B C. A C.B
3 k. A .B A. k.B k. A.B
Prof. Neydiwan - Matemática

16. Propriedades de Matrizes
t t
1 A A
t t t
2 A B A B
t t
3 k.A k.A
t t t
4 A.B B .A
Prof. Neydiwan - Matemática

17. Inversão de Matrizes
Seja A uma matriz quadrada. Dizemos que A é matriz
inversível se existir uma matriz B tal que A.B = B.A = I.
1
A. A In
Calcule a inversa da matriz A =
Resolvendo os sistemas temos a matriz inversa de A.
Prof. Neydiwan - Matemática

18. Resolução de Exercícios
Prof. Neydiwan - Matemática