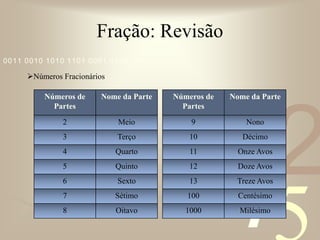
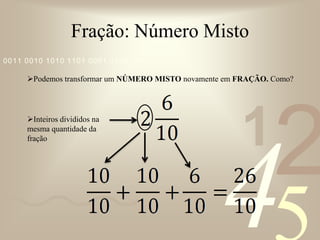
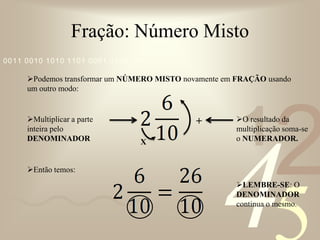
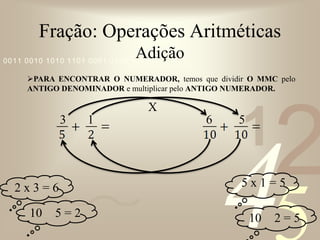
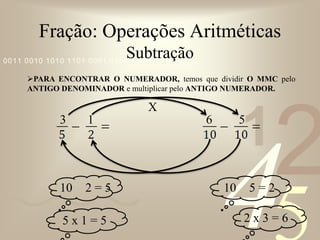
O documento discute conceitos básicos de frações, incluindo: (1) exemplos do uso de frações no dia-a-dia, como dividir pizza ou bolo; (2) os termos numerador e denominador; (3) tipos de frações como própria, imprópria e aparente; (4) frações equivalentes; (5) número misto; (6) simplificação de frações; e (7) operações com frações como adição, subtração, multiplicação e divisão.

1. FraçãoParte ou pedaço de um inteiro.Exemplos do Uso da Fração no Dia-a-Dia Ao dividir uma pizza;Exemplos do Uso da Fração no Dia-a-DiaAo dividir um bolo;Exemplos do Uso da Fração no Dia-a-DiaNa contagem das raças de um país;Fração: RevisãoNúmeros FracionáriosFração: RevisãoATENÇÃO: A partir do número ONZE, dizemos o número em cardinal seguido da palavra AVOS, exemplos:Três Quinze AvosOito Trinta e Dois Avos

2. Fração: RevisãoATENÇÃO: O número que está embaixo – números de divisões – é chamado de DENOMINADOR.

3. O número que está em cima – número de partes escolhidas – é chamado de numerador.numeradorDENOMINADOR

4. Fração: Revisãofração própria: O numerador é menor que o denominador;

5. fração imprópria: O numerador é maior que o denominador;

6. fração aparente: O numerador é múltiplo do denominador;Fração: Revisãofrações Equivalentes: Quando 2 ou mais frações tem a mesma quantidade “pegas” de um mesmo todos.

7. Se comemos de pizza é o mesmo que comermos ou de pizza.Fração: Número MistoComo representar DUAS PIZZAS faltando pedaços em uma FRAÇÃO?

8. RESPOSTA: Utilizando o NÚMERO MISTO – Um número formado por um número inteiro junto de uma fração.Fração: Número MistoUm bolo inteiro mais um pedaço do bolo do mesmo tamanho, podemos dizer que temos: de bolo de fubá

9. Fração: Número MistoParte InteiraParte Fracionária ou Fração

10. Fração: Número MistoPodemos transformar um NÚMERO MISTO novamente em FRAÇÃO. Como?

11. Inteiros divididos na mesma quantidade da fraçãoFração: Número MistoPodemos transformar um NÚMERO MISTO novamente em FRAÇÃO usando um outro modo:

12. Multiplicar a parte inteira pelo DENOMINADOR

13. O resultado da multiplicação soma-se o NUMERADOR.+XEntão temos:

14. LEMBRE-SE: O DENOMINADOR continua o mesmo.Fração: Simplificação da FraçãoO que é mais fácil? Repartir uma multidão em OITO GRUPOS e escolher DOIS?Fração: Simplificação da FraçãoOu repartir uma multidão em QUATRO GRUPOS e escolher UM?Fração: Simplificação da FraçãoSe o divisor é menor possível, a divisão fica mais fácil!!! Então é melhor simplificar a fração.

15. Quando temos a fração quando numeradores e denominadores GRANDES, o melhor a fazer são simplificá-los. COMO? OU Basta escolher um número que DIVIDE O NUMERADOR E O DENOMINADOR AO MESMO TEMPO.

16. Quanto MENOR a fração MELHOR a simplificação.: 2: 4: 2: 4

17. Fração: Simplificação da FraçãoSe não temos como simplificar mais a fração ou não conseguimos simplificá-la de início. OUTemos uma FRAÇÃO IRREDUTÍVEL, que não se pode mais SIMPLIFICAR.: 2: 4: 2: 4

18. Fração: Operações AritméticasAdiçãoCarlos comprou uma barra de chocolate e comeu dois pedaços. Maria comprou uma barra de chocolate igual a de Carlos, mas ela só comeu um pedaço. Eles decidiram juntar a duas barras. Quantos pedaços eles tem? E quantas frações eles tem? Carlos Maria

19. Fração: Operações AritméticasAdiçãoCarlos comprou uma barra de chocolate e comeu dois pedaços. Maria comprou uma barra de chocolate igual a de Carlos, mas ela só comeu um pedaço. Eles decidiram juntar a duas barras. Quantos pedaços eles tem? E quantas frações eles tem? Carlos Maria

20. Fração: Operações AritméticasAdiçãoMaria tem da barra de chocolate.

21. Carlos tem da barra de chocolate. Carlos Maria

22. Fração: Operações AritméticasAdiçãoJunto eles tem: 9 PEDAÇOS OUFração: Operações AritméticasAdiçãoQuando os DENOMINADORES SÃO IGUAIS, BASTA SOMAR OS NUMERADORES.Fração: Operações AritméticasAdiçãoQuando os DENOMINADORES SÃO DIFERENTES, TEMOS SEGUINTES REGRAS A SEGUIR.Fração: Operações AritméticasAdiçãoPRIMEIRO, DEVE ENCONTRA O MÍNIMO MÚLTIPLO COMUM DOS DENOMINADORES. 5 , 2 2 5 , 1 5 1 , 1 10O VALOR DO M.M.C. (10) SUBSTITUIRÁ OS DENOMINADORES ANTIGOS (5 E 2).Fração: Operações AritméticasAdiçãoPARA ENCONTRAR O NUMERADOR, temos que dividir O MMC pelo ANTIGO DENOMINADOR e multiplicar pelo ANTIGO NUMERADOR.X3165÷5 x 1 = 52 x 3 = 610 ÷ 5 = 210 ÷ 2 = 5

23. Fração: Operações AritméticasAdiçãoPOR FIM, SOMA-SE OS “NOVOS” NUMERADORES, repetindo o DENOMINADOR.Fração: Operações AritméticasSubtraçãoQuando os DENOMINADORES SÃO DIFERENTES, TEMOS QUE SEGUIR AS MESMAS REGRAS DA ADIÇÃO.Fração: Operações AritméticasSubtraçãoPRIMEIRO, DEVE ENCONTRA O MÍNIMO MÚLTIPLO COMUM DOS DENOMINADORES. 5 , 2 2 5 , 1 5 1 , 1 10O VALOR DO M.M.C. (10) SUBSTITUIRÁ OS DENOMINADORES ANTIGOS (5 E 2).Fração: Operações AritméticasSubtraçãoPARA ENCONTRAR O NUMERADOR, temos que dividir O MMC pelo ANTIGO DENOMINADOR e multiplicar pelo ANTIGO NUMERADOR.X3165÷10 ÷ 5 = 210 ÷ 2 = 52 x 3 = 65 x 1 = 5

24. Fração: Operações AritméticasSubtraçãoPOR FIM, SOMA-SE OS “NOVOS” NUMERADORES, repetindo o DENOMINADOR.Fração: Operações AritméticasMultiplicaçãoCoralina comprou um terreno onde DOIS TERÇOS do terreno foi construído a casa. Em UM QUINTO do restante foi construído um jardim e em QUATRO QUINTOS uma piscina. Em relação ao terreno todo quanto foi ocupado pelo jardim? Quanto foi ocupado pela piscina?Fração: Operações AritméticasMultiplicaçãoO que restou para o jardim e para piscina foi apenas um terço. Quando REPARTIMOS uma fração estamos MULTIPLICANDO OS ESPAÇOS.Fração: Operações AritméticasMultiplicaçãoO que restou para o jardim e para piscina foi apenas um terço. Quando REPARTIMOS uma fração estamos MULTIPLICANDO OS ESPAÇOS.JARDIMCASAPISCINA

25. Fração: Operações AritméticasMultiplicaçãoComo descobrir qual parte caberá ao jardim e qual caberá à piscina??????????????JARDIM???CASA??PISCINA??????

26. Fração: Operações AritméticasMultiplicaçãoBasta multiplicar o que restou para o jardim pelo o pedaço que o jardim vai ocupar. NUMERADOR VEZES NUMERADOR e DENOMINADOR VEZES DENOMINADOR.

27. Basta multiplicar o que restou para a piscina pelo o pedaço que a piscina vai ocupar. NUMERADOR VEZES NUMERADOR e DENOMINADOR VEZES DENOMINADOR.Fração: Operações AritméticasDivisãoJoaquim comprou uma caixa DIVIDIDA EM 4 PARTES para guardar carrinhos de brinquedo. Cada carrinho tem UM OITAVO DO TAMANHO DA CAIXA, então quantos carrinhos de brinquedo cabem em cada parte da caixa?Fração: Operações AritméticasDivisãoComo dividir UM QUARTO da caixa pelo UM OITAVO (tamanho do carrinho de brinquedo??

28. Fração: Operações AritméticasDivisãoSOLUÇÃO: Temos uma regra: Repete a primeira fração;Inverta a segunda fração (denominador vai para o lugar do numerador e o numerador vai para o lugar do denominador);E por fim, multiplique as frações. =X

29. Fração: Operações AritméticasDivisãoComo saber quanto a FRAÇÃO RESULTANTE (O RESULTADO) representa em questão de espaço?

30. SOLUÇÃO: Basta dividir o NUMERADOR PELO DENOMINADOR!

31. Então, cabem 2 carrinhos de brinquedo em cada parte da caixa.

32. ATENÇÃO: Se não der para dividir apenas simplifique a fração resultante.2?

33. Fração: Operações AritméticasDivisãoEm cada parte cabem 2 carrinhos de brinquedos.