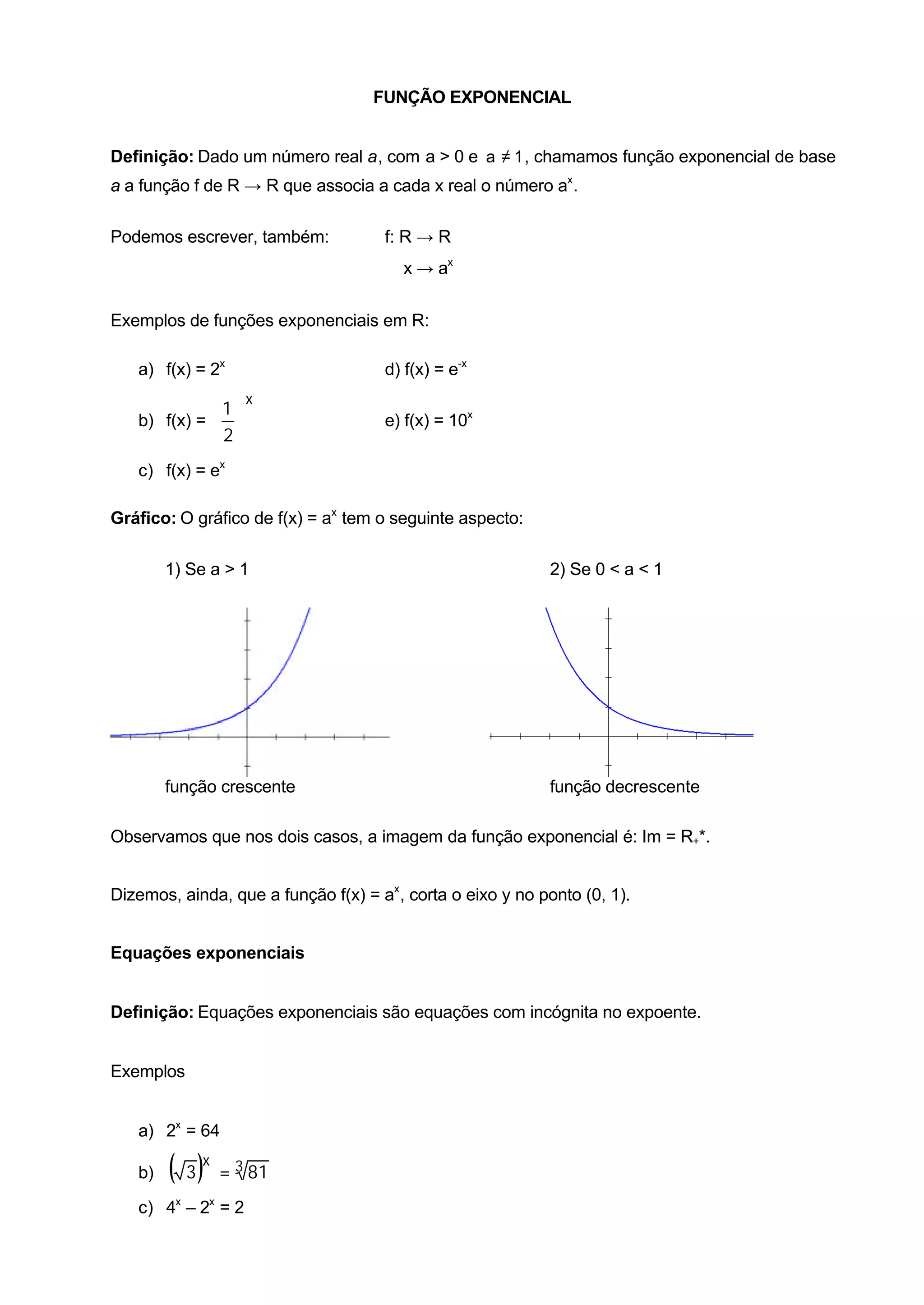
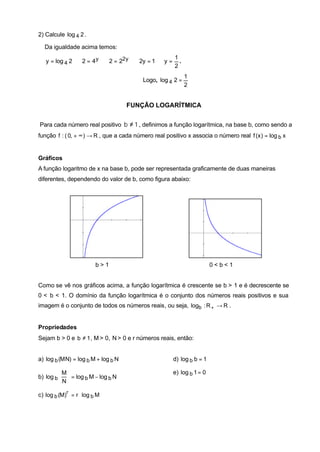
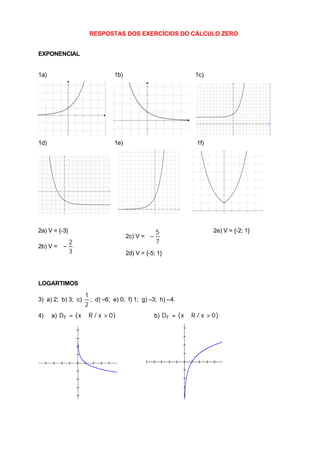
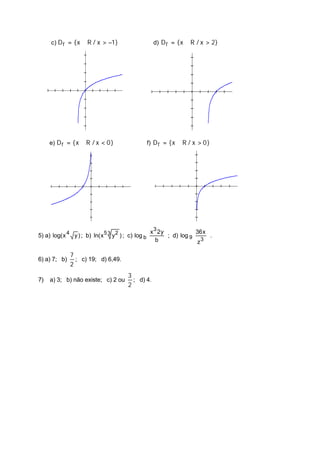
1) O documento apresenta os conceitos de função exponencial e logarítmica, incluindo suas definições, gráficos e propriedades. 2) É dado um exemplo numérico de cálculo de logaritmo e outro de aplicação de logaritmo na resolução de um problema de juros compostos. 3) São fornecidos exercícios sobre esboço de gráficos, resolução de equações exponenciais e cálculo de logaritmos para fixação dos conceitos apresentados.

1. FUNÇÃO EXPONENCIAL
Definição: Dado um número real a, com a > 0 e a ≠ 1 , chamamos função exponencial de base
a a função f de R → R que associa a cada x real o número ax .
Podemos escrever, também: f: R → R
x → ax
Exemplos de funções exponenciais em R:
a) f(x) = 2x d) f(x) = e-x
x
1 
b) f(x) =   e) f(x) = 10x
2
c) f(x) = ex
Gráfico: O gráfico de f(x) = ax tem o seguinte aspecto:
1) Se a > 1 2) Se 0 < a < 1
função crescente função decrescente
Observamos que nos dois casos, a imagem da função exponencial é: Im = R+*.
Dizemos, ainda, que a função f(x) = ax , corta o eixo y no ponto (0, 1).
Equações exponenciais
Definição: Equações exponenciais são equações com incógnita no expoente.
Exemplos
a) 2x = 64
b) ( 3 )x = 3 81
c) 4x – 2x = 2

2. Para resolvermos essas equações, devemos reduzir ambos os membros em potências de
mesma base, usando para isso as propriedades de potência.
Pelo fato da função exponencial f(x) = ax ser injetora, podemos concluir que potências iguais e
de mesma base têm os expoentes iguais, ou seja:
ab = ac ⇔ b = c (a > 0 e a ≠ 1 )
Exemplos
a) 2x = 64 b) ( 3 )x = 3 81 c) 4x – 2x = 2
2x = 26 (3 )
1 /2 x
= (81)1 / 3 22x – 2x – 2 = 0
1 1
x
x=6 3 2 = (34 ) 3 fazendo 2x = t
1 4
x
V = {6} 3 2 = 33 t2 – t – 2 = 0
1 4
x= temos que t = – 1 ou t = 2
2 3
8
x= 2x = – 1 ou 2x = 2
3
8
V={ } ∃ x / 2x = – 1
/
3
2x = 21
x=1
V = {1}
LOGARITMOS
Definição: Seja b ≠ 1 um número real positivo. Dado um número positivo x qualquer,
existe um único número real y tal que x = b y . Este número y é chamado logaritmo do
número x na base b e será denotado por y = log b x .
Temos, então, a igualdade: y = log b x ⇔ x = b y
Exemplos:
1) Calcule log 3 9 .
Da igualdade acima temos:
y = log 3 9 ⇔ 9 = 3 y ⇔ 3 2 = 3 y ⇔ y = 2 .
Logo, log 3 9 = 2

3. 2) Calcule log 4 2 .
Da igualdade acima temos:
1
y = log 4 2 ⇔ 2 = 4 y ⇔ 2 = 22 y ⇔ 2y = 1 ⇔ y = .
2
1
Logo, log 4 2 =
2
FUNÇÃO LOGARÍTMICA
Para cada número real positivo b ≠ 1 , definimos a função logarítmica, na base b, como sendo a
função f : ( 0, + ∞ ) → R , que a cada número real positivo x associa o número real f (x ) = log b x
Gráficos
A função logaritmo de x na base b, pode ser representada graficamente de duas maneiras
diferentes, dependendo do valor de b, como figura abaixo:
b>1 0<b<1
Como se vê nos gráficos acima, a função logarítmica é crescente se b > 1 e é decrescente se
0 < b < 1. O domínio da função logarítmica é o conjunto dos números reais positivos e sua
imagem é o conjunto de todos os números reais, ou seja, logb : R + → R .
Propriedades
Sejam b > 0 e b ≠ 1 , M > 0, N > 0 e r números reais, então:
a) log b (M N) = log b M + log b N d) log b b = 1
 M e) log b 1 = 0
b) log b   = log b M − log b N
 N
c) log b (M)r = r ⋅ log b M

4. Mudança de base
Sejam a e b números reais positivos com a ≠ 1 e b ≠ 1 , para qualquer número real positivo M
temos a igualdade:
log a M
log b M =
log a b
Exemplo
Escreva a seguinte expressão log 6 x + 2 log 6 y − 3 log 6 z com um único logaritmo.
xy 2
Solução: log 6 x + 2 log 6 y − 3 log 6 z = log 6 x + log 6 y 2 − log 6 z 3 = log 6
z3
Logaritmos especiais
Dois logaritmos possuem notações próprias que são:
• f (x ) = log10 x , que será denotado simplesmente por f (x ) = log x e será chamado
logaritmo decimal (na base 10).
• f (x ) = log e x , que será denotado simplesmente por f (x ) = ln x e será chamado logaritmo
natural (ou Neperiano), onde e representa o número de Napier, base da função
exponencial g( x ) = e x , cujo valor aproximado é e = 2,7182...
Relação entre função logarítmica e função exponencial:
As funções f (x ) = log b x e g( y ) = b y são funções inversas, uma da outra, pois pela própria
definição de logaritmo temos, log b x = y ⇔ x = b y e, assim,
g(f ( x )) = g(log b x ) = blog b x = x e
( )
f (g( y )) = f b y = log b (b y ) = y

5. Exemplo
Durante quanto tempo devemos investir R$ 900,00 a uma taxa de 10% ao ano, no sistema de
juros compostos, para resgatar R$ 1.500,00?
Solução:
Da fórmula de juros composto, PF = PV(1 + i) t , onde PF é o valor a ser resgatado, PV é o
valor aplicado, i é a taxa e t é o tempo de aplicação, temos que:
t
 10  t 1500 5  5  log(5 / 3) 0,2219
1500 = 9001 +  ⇔ (1 + 0,1) = ⇔ (11)t = ⇔ t = log1,1  =
, = = 5,3599
 100  900 3  3 log(1,1) 0,0414

6. EXERCÍCIOS SOBRE EXPONENCIAL E LOGARITMO
1) Esboce o gráfico das seguintes funções:
a) f(x) = 2x x
x
1 
d) f(x) =   - 3
1  2
b) f(x) =  
2 e) f(x) = 3.2x
c) f(x) = 2x + 2 x
f) f(x) = 2
2) Resolva as seguintes equações exponenciais:
x d) (2x )x + 4 = 32
1 
a)   = 125 e) 4x + 1 – 9.2x + 2 = 0
5 
b) 125x = 0,04
2x + 3
 1 
c) 5 3x-1
= 
 25 
3) Calcule o valor do logaritmo dado.
1
a) log 8 64 b) log 4 64 c) log 64 8 d) log 2
64
e) log 2 1 f) log 2 2 g) log 1 8 h) log 1 81
2 3
4) Determine o domínio e faça um esboço do gráfico da função dada.
a) f (x ) = log 1 x b) f (x ) = log 2 x c) f (x ) = ln( x + 1)
4
d) f (x ) = ln( x − 2) e) f (x ) = log 1 (− x ) f) f (x ) = − log 1 x
2 3
5) Reduza a expressão dada em um único logaritmo.
1 2
a) 4 log x + log y b) 5 ln x + ln y − 3 log 6 1
2 3
c) 3 log b ( x ) + log b (2y ) − 1 d) log 9 x + log 3 6 − 3 log 9 z
3
6) Sendo ln a = 2, ln b = 5, ln = −0,51 , calcule.
5
3b 2
a) ln(ab ) b) ln ab c) ln(a 2 b3 ) d) ln( )
3
5 a
7) Resolva as seguintes equações:
a) ln x + ln 3 = ln 9 c) ln x − ln( x − 1) = ln 2 + ln( 3 − x )
b) ln (x − 2x 2 ) + ln 4 = 0 d) ln x 2 − ln x − ln 4 = 0

7. RESPOSTAS DOS EXERCÍCIOS DO CÁLCULO ZERO
EXPONENCIAL
1a) 1b) 1c)
1d) 1e) 1f)
2a) V = {-3}  5 2e) V = {-2; 1}
2c) V = − 
 2  7
2b) V = − 
 3 2d) V = {-5; 1}
LOGARTIMOS
1
3) a) 2; b) 3; c) ; d) –6; e) 0; f) 1; g) –3; h) –4.
2
4) a) D f = {x ∈ R / x > 0} b) D f = {x ∈ R / x > 0}

8. c) D f = {x ∈ R / x > −1} d) D f = {x ∈ R / x > 2}
e) D f = {x ∈ R / x < 0} f) D f = {x ∈ R / x > 0}
 x3 2y 
5) a) log( x 4 y ) ; b) ln( x 5 3 y 2 ) ; c) log b   ; d) log  36 x  .
 b  9 3 
 
   z 
7
6) a) 7; b) ; c) 19; d) 6,49.
2
3
7) a) 3; b) não existe; c) 2 ou ; d) 4.
2