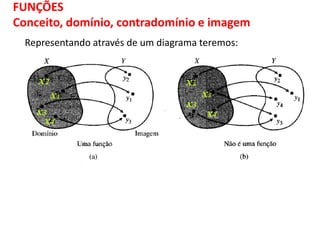
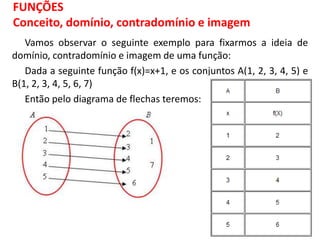
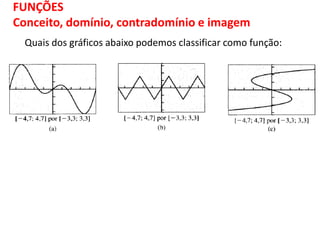
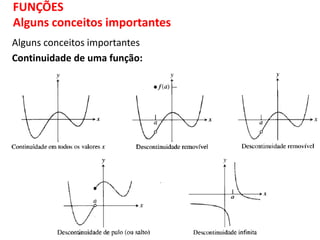
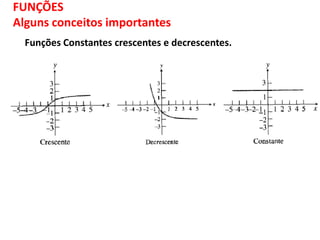
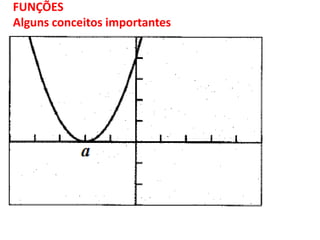
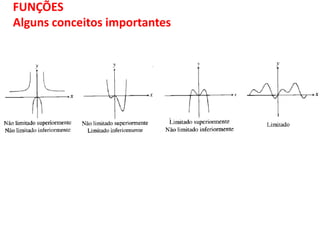
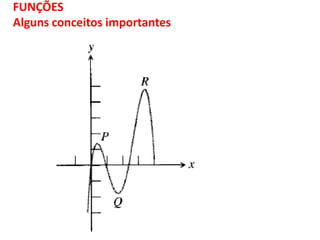
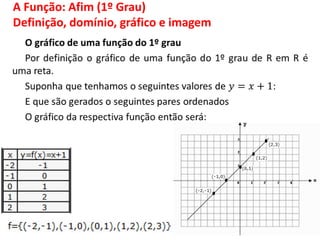
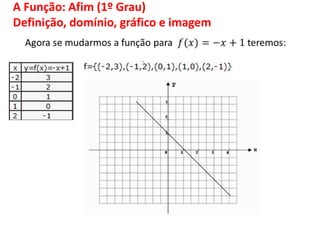
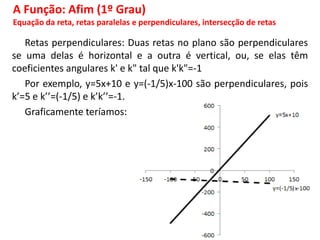
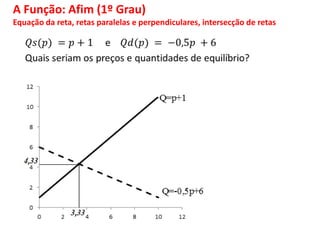
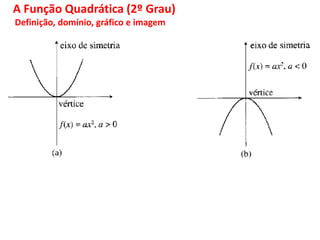
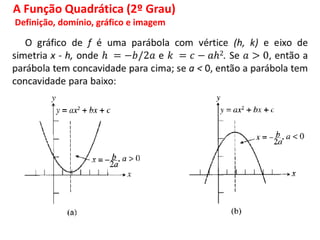
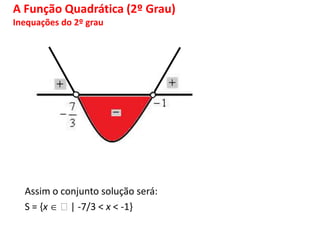
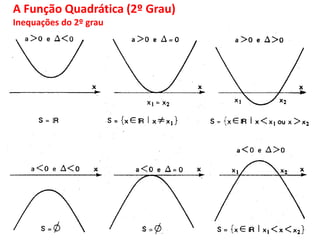
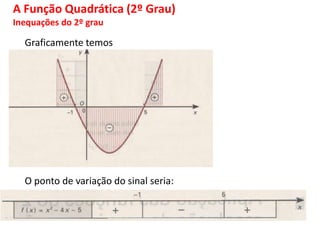
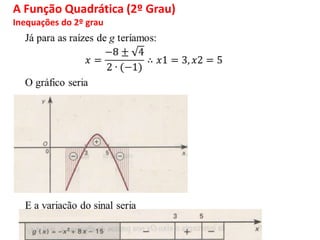
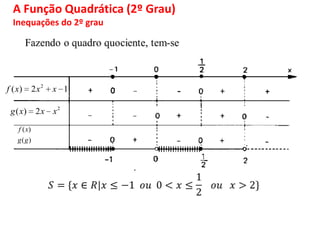
O documento discute funções matemáticas, incluindo conceitos como domínio, contradomínio e imagem. Apresenta exemplos de funções afins e quadráticas, mostrando como representá-las graficamente e resolvendo equações e inequações do primeiro e segundo grau.