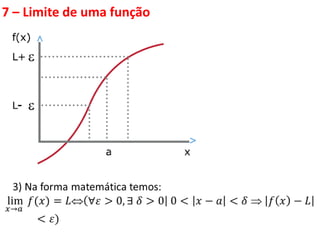
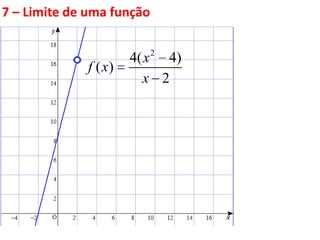
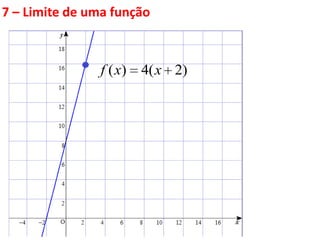
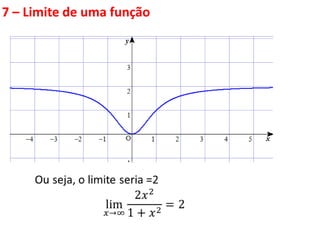
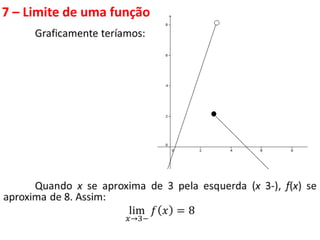
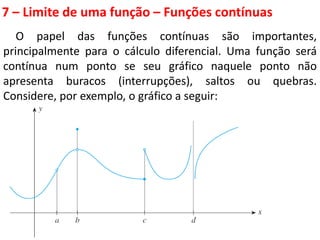
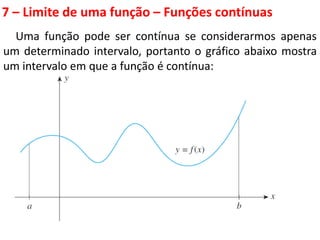
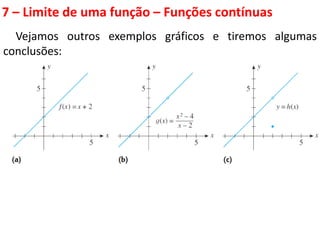
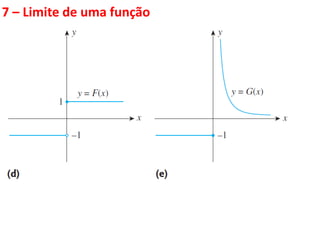
Este documento discute limites de funções. Explica que limites são fundamentais para o cálculo diferencial e integral e define limites como algo que ocorre fora do mundo físico, necessitando de modelos matemáticos. Apresenta propriedades de limites e funções contínuas, destacando que uma função é contínua em um ponto se seu gráfico não apresenta descontinuidades nesse ponto.

1. Matemática I
Tópico 07– Limites de uma Função
Ricardo Bruno N. dos Santos
Professor Faculdade de Economia
e do PPGE (Economia) UFPA
UNIVERSIDADE FEDERAL DO PARÁ
INSTITUTO DE CIÊNCIAS SOCIAIS APLICADAS – ICSA
FACULDADE DE ECONOMIA

2. Limite

3. 7 – Limite de uma função
Conceito:
O conceito de limite de uma função é básico para o estudo
de cálculo. Seu papel é muito importante em toda teoria
matemática envolvida com o Cálculo Diferencial e Integral. Há
uma cadeia ordenada muito bem estabelecida no Cálculo:
Conjuntos, Funções, Limites, Continuidade, Derivadas e
Integrais
O motivo para isto é que nem tudo o que queremos
realizar, ocorre no meio físico e quase sempre é necessário
introduzir um modelo que procura algo que está fora das
coisas comuns e esta procura ocorre com os limites nos
estudos de sequências, séries, cálculos de raízes de funções,
...

4. 7 – Limite de uma função

5. 7 – Limite de uma função

6. 7 – Limite de uma função

7. 7 – Limite de uma função

8. 7 – Limite de uma função

9. 7 – Limite de uma função
Propriedades

10. 7 – Limite de uma função
Propriedades

11. 7 – Limite de uma função

12. 7 – Limite de uma função

13. 7 – Limite de uma função
2
4( 4)
( )
2
x
f x
x

14. 7 – Limite de uma função
( ) 4( 2)f x x

15. 7 – Limite de uma função

16. 7 – Limite de uma função

17. 7 – Limite de uma função

18. 7 – Limite de uma função

19. 7 – Limite de uma função

20. 7 – Limite de uma função

21. 7 – Limite de uma função

22. 7 – Limite de uma função

23. Funções Contínuas

24. 7 – Limite de uma função – Funções contínuas
O papel das funções contínuas são importantes,
principalmente para o cálculo diferencial. Uma função será
contínua num ponto se seu gráfico naquele ponto não
apresenta buracos (interrupções), saltos ou quebras.
Considere, por exemplo, o gráfico a seguir:

25. 7 – Limite de uma função – Funções contínuas

26. Uma função pode ser contínua se considerarmos apenas
um determinado intervalo, portanto o gráfico abaixo mostra
um intervalo em que a função é contínua:
7 – Limite de uma função – Funções contínuas

27. Vejamos outros exemplos gráficos e tiremos algumas
conclusões:
7 – Limite de uma função – Funções contínuas

28. 7 – Limite de uma função

29. 7 – Limite de uma função – Funções contínuas

30. 7 – Limite de uma função – Funções contínuas

31. FIM DO TÓPICO