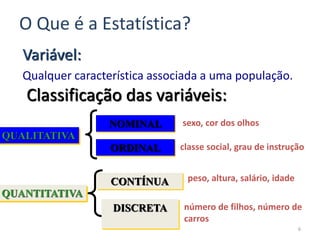
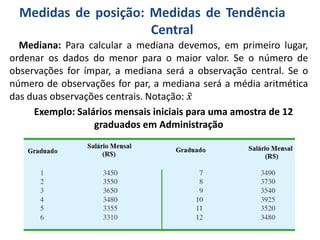
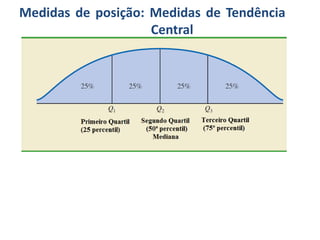
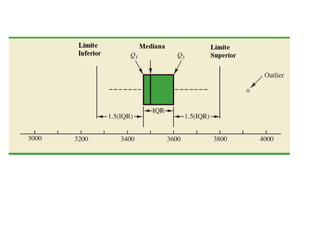
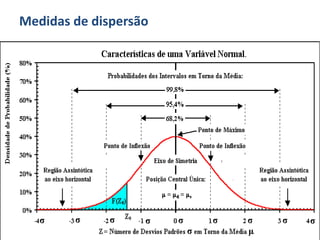
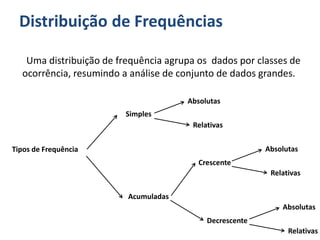
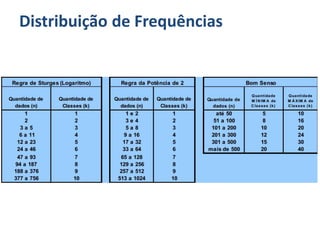
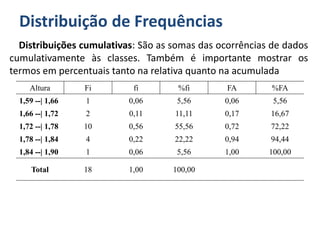
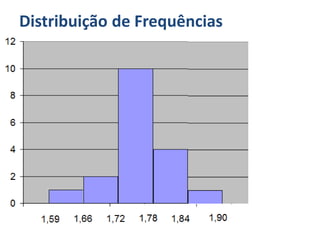
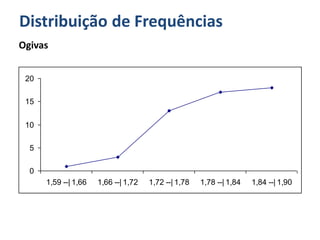
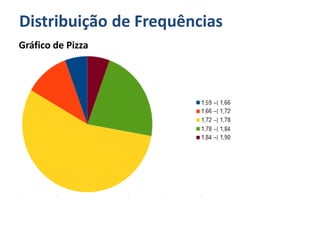
O documento discute o que é estatística, descrevendo sua evolução histórica e como se desenvolveu como área do conhecimento no século XX. Também apresenta medidas estatísticas comuns como média, mediana e desvio padrão, além de explicar distribuições de frequência e como organizar dados em grupos.













































![Distribuição de Frequências
Com relação a Variância para dados agrupados em classes, pode-se utilizar a
seguinte expressão a partir dos desvio padrão:
𝑠 =
1
𝑛 − 1
𝑖=1
𝑛
𝑥𝑖 − 𝑥 2 𝑓𝑎
Onde
n – Nº de Observações
𝑥𝑖 − 𝑥 2 - Os desvios em torno da média ao quadrado. Onde 𝑥𝑖 são os pontos
médios de cada classe;
𝑓𝑎 - Frequências absolutas de cada classe.
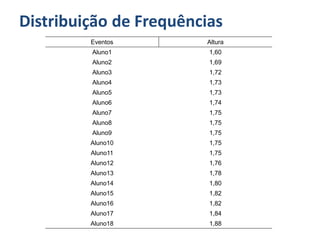
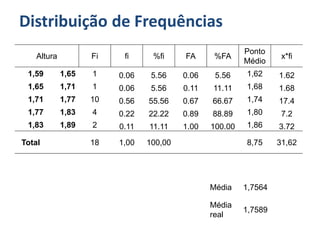
Para as alturas temos:
𝑠 =
1
18 − 1
{ 1,62 − 1,76 2 × 1 + 1,68 − 1,76 2 × 1 + 1,74 − 1,76 2 × 10 + 1,8 − 1,76 2 × 4 + [ 1,86 − 1,76 2 × 2]
s=0,058
𝑠2
= 0,03](https://image.slidesharecdn.com/01-estatsticadescritiva-140320033450-phpapp02/85/Estatistica-Descritiva-60-320.jpg)