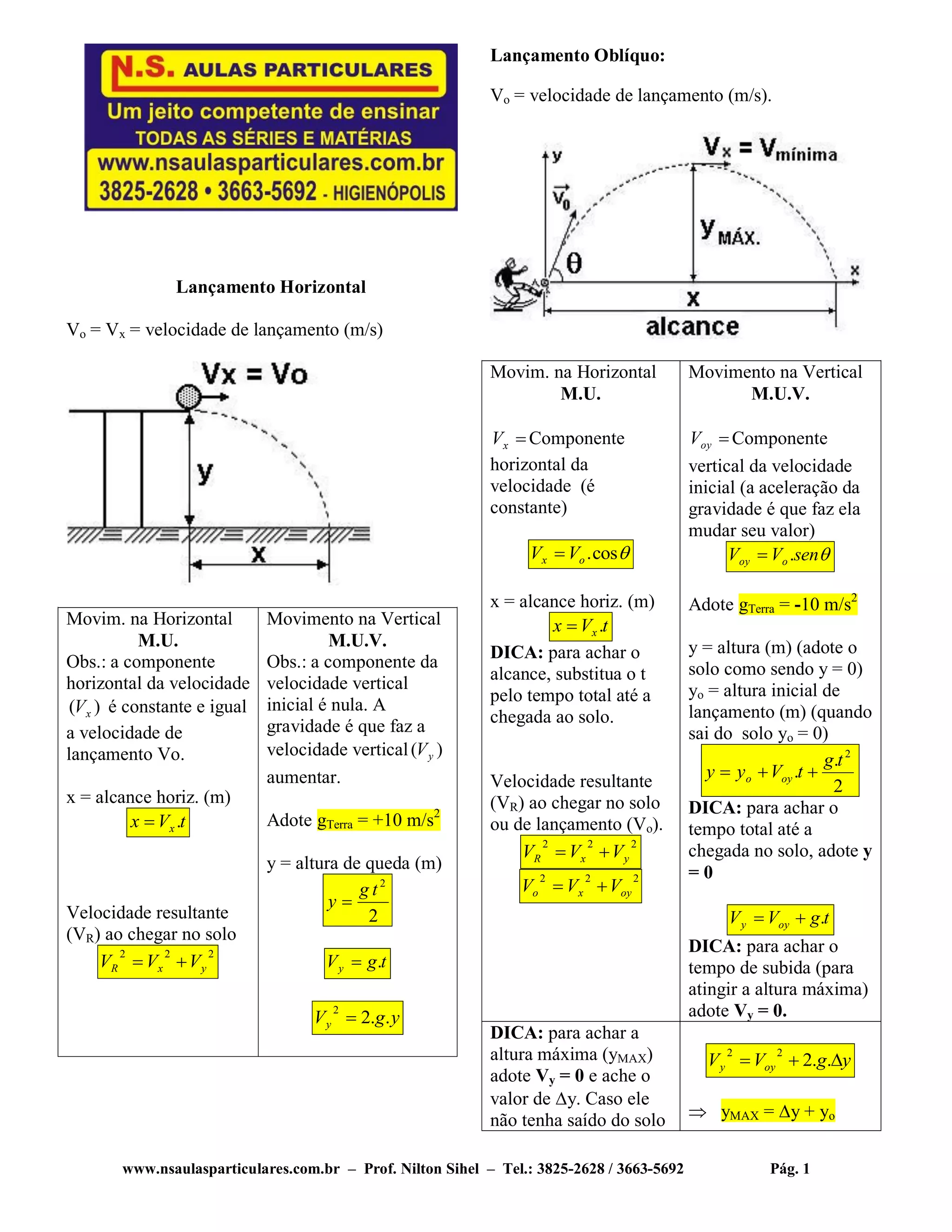
O documento apresenta as equações fundamentais para modelar o movimento de objetos lançados em diferentes situações: lançamento horizontal, lançamento vertical e lançamento oblíquo. Fornece as expressões para calcular a velocidade, altura, tempo e alcance horizontal em função da velocidade inicial, aceleração da gravidade e ângulo de lançamento.

1. www.nsaulasparticulares.com.br – Prof. Nilton Sihel – Tel.: 3825-2628 / 3663-5692 Pág. 1
Lançamento Horizontal
Vo = Vx = velocidade de lançamento (m/s)
Movim. na Horizontal
M.U.
Obs.: a componente
horizontal da velocidade
)( xV é constante e igual
a velocidade de
lançamento Vo.
x = alcance horiz. (m)
tVx x .
Velocidade resultante
(VR) ao chegar no solo
222
yxR VVV 
Movimento na Vertical
M.U.V.
Obs.: a componente da
velocidade vertical
inicial é nula. A
gravidade é que faz a
velocidade vertical )( yV
aumentar.
Adote gTerra = +10 m/s2
y = altura de queda (m)
2
2
tg
y 
tgVy .
ygVy ..2
2

Lançamento Oblíquo:
Vo = velocidade de lançamento (m/s).
Movim. na Horizontal
M.U.
xV Componente
horizontal da
velocidade (é
constante)
cos.ox VV 
x = alcance horiz. (m)
tVx x .
DICA: para achar o
alcance, substitua o t
pelo tempo total até a
chegada ao solo.
Velocidade resultante
(VR) ao chegar no solo
ou de lançamento (Vo).
222
yxR VVV 
222
oyxo VVV 
Movimento na Vertical
M.U.V.
oyV Componente
vertical da velocidade
inicial (a aceleração da
gravidade é que faz ela
mudar seu valor)
senVV ooy .
Adote gTerra = -10 m/s2
y = altura (m) (adote o
solo como sendo y = 0)
yo = altura inicial de
lançamento (m) (quando
sai do solo yo = 0)
2
.
.
2
tg
tVyy oyo 
DICA: para achar o
tempo total até a
chegada no solo, adote y
= 0
tgVV oyy .
DICA: para achar o
tempo de subida (para
atingir a altura máxima)
adote Vy = 0.
DICA: para achar a
altura máxima (yMAX)
adote Vy = 0 e ache o
valor de y. Caso ele
não tenha saído do solo
ygVV oyy  ..2
22
 yMAX = y + yo