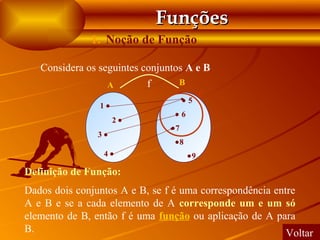
Este documento fornece uma introdução às funções matemáticas, incluindo definições de termos-chave como domínio, contradomínio, gráficos de funções, zeros de funções, monotonia e injectividade. Explica como interpretar e analisar graficamente diferentes aspectos e propriedades de funções.

1. Resolução de problemas
Aplicações da teoria de
Conjuntos

2. Resolução:

3. Resolução:

4. Resolução:

5. Continuação

6. Resolução

7. Resolução

8. Funções
1. Interpretação de Gráficos
O gráfico representa a viagem da Joana num dia em que resolveu
visitar uns amigos
Distância
( Km)
Tempo
(horas)
Voltar

9. Funções
1. Noção de Função
Considera os seguintes conjuntos A e B
A f B
C
•5
1•
•6
2•
•7
3•
•8
4• •9
Definição de Função:
Dados dois conjuntos A e B, se f é uma correspondência entre
A e B e se a cada elemento de A corresponde um e um só
elemento de B, então f é uma função ou aplicação de A para
B. Voltar

10. Funções
1. Noção de Função
•A esta correspondência chama-se _________.
função
•Ao conjunto A chamamos conjunto de partida ou _________________
Domínio
e representa-se por ______. Df = {
Df 1, 2, 3, 4 }
•A todo o elemento de A chamamos _____________.
Objectos
•Ao conjunto B chamamos _______________________ da função.
Conjunto de Chegada
Conjunto de chegada de f = { 5, 6, 7, 8, 9 }
•A todo o elemento de B ao qual corresponde um elemento de A
imagem
chamamos ___________.
Estabelece o conjunto C formado pelas imagens dos elementos de A
contradomínio
• Ao conjunto C chamamos ______________ da função e representa-se
D’f 5, 6, 7 Voltar

11. Funções
1. Noção de Função
Simboliza-se do seguinte modo:
f: A B
x y=f(x)
• x é variável independente e y a variável dependente
• Ao conjunto A chamamos Domínio e representa-se por Df
• Ao conjunto B chamamos Conjunto de Chegada
• Ao conjunto das imagens chama-se Contradomínio da função e
representa-se por D‘f
• A cada objecto x corresponde uma e uma só imagem y=f(x);

12. Funções
1. Interpretação de diagramas
Exemplo 1:
A correspondência não é uma função porque o objecto 1 tem duas
imagens, 4 e 5, logo mais do que uma imagem.
Exemplo 2:
A correspondência não é uma função porque o objecto 2 não tem
imagens.

13. Funções
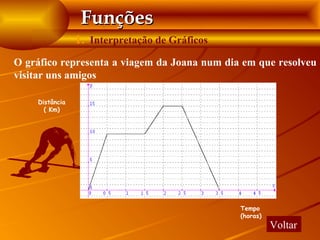
2. Representação gráfica de uma Função
Num determinado dia registaram-se as temperaturas de ar
na cidade de Aveiro, de hora a hora e, a partir delas,
elaborou-se o gráfico das temperaturas em função da hora do
dia.
Temperatura
º
C
Horas
Indique: • os intervalos de tempo onde a
1 [0;24] 4
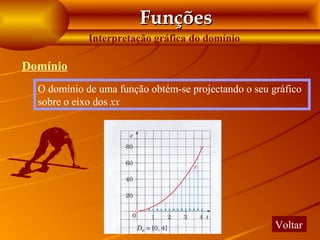
• o domínio; temperatura: - é positiva; - é negativa;
• os intervalos onde a temperatura:
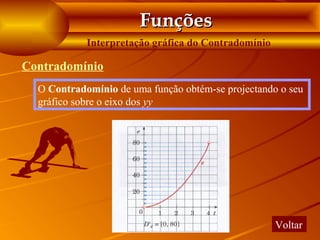
• o contradomínio; 2 [-3;6] -aumenta; -aumenta e é positiva; -
• as horas do dia em que se registou
5
diminui; - diminui e é positiva; - é
3
a temperatura 0ºC constante;

14. Funções
2. Representação gráfica de uma Função
• Como averiguar se se trata de uma função
Um gráfico de uma função só pode ser intersectado no
máximo uma vez por uma qualquer recta vertical.
Não se trata de uma
representação de uma Trata-se de uma representação de uma
função função

15. Funções
Interpretação gráfica do domínio
Domínio
O domínio de uma função obtém-se projectando o seu gráfico
sobre o eixo dos xx
Voltar

16. Funções
Interpretação gráfica do Contradomínio
Contradomínio
O Contradomínio de uma função obtém-se projectando o seu
gráfico sobre o eixo dos yy
Voltar

17. Funções
3. Noções gerais de uma função
• Zeros de uma função
Definição: Zero de uma função é todo o
objecto que tem imagem nula.
DDeterminação dos zeros de uma função:
Graficamente
Averiguar as abcissas dos pontos do gráfico para
os quais o gráfico da função intersecta o
eixo das abcissas ( xx )
Analiticamente
Determinar os valores de x para os quais f(x)=0 zeros
isto é, x: f (x)=0
Voltar

18. Funções
3. Noções gerais de uma função
• Sinal de uma função
Definição : Seja f uma função de domínio D, dizemos que :
- f é positiva em I (I⊂ D) se e só se f(x) > 0, para todo o x∈I.
- f é negativa em I (I⊂ D) se e só se f(x) < 0, para todo o x∈I.
DDeterminação do sinal de uma função:
Graficamente
-A função é positiva para todos os valores de x cujas
imagens estão acima do eixo das abcissas.
f(x) >0
-A função é negativa para todos os valores de x f(x) < 0
cujas imagens estão abaixo do eixo das abcissas.
Voltar

19. Funções
Noções gerais de uma função
• Monotonia de uma função
f(b) g(b) g f(b) g(b) g
f
f
g(a)
f(a) f(a)
g(a)
O a b O a b
a b a b
A função f é crescente A função g é decrescente A função f é
A função g é estritamente
estritamente crescente decrescente num intervalo
num intervalo E. num intervalo E. num intervalo E. E.
Definição : Diz-se que f é crescente / estritamente crescente em E⊂Df se para todos os
números reais a e b pertencentes a E, se a < b, então f(a)≤f(b) / se a < b, então f(a)< f(b).
Definição : Diz-se que g é decrescente / estritamente decrescente em E⊂Df se para
todos os números reais a e b pertencentes a E, se a < b então g(a) ≥ g(b) / se a < b, então
g(a)>g(b).
Definição : Uma função crescente ou decrescente diz-se monótona. Voltar

20. Funções
Noções gerais de uma função
• Monotonia de uma função
Definição : Seja f uma função de domínio D.
f(a) é um máximo absoluto de f se, para todo o x pertencente a D, f(a) ≥ f(x)
f(b) é um mínimo absoluto de f se, para todo o x pertencente a D, f(b) ≤f(x)
Definição : Seja f uma função de domínio D.
f(a) é um máximo relativo de f se existir um intervalo aberto E contendo a tal que
f(a) ≥ f(x), qualquer que seja o x ∈ E ∩ D
f(b) é um mínimo relativo de f se existir um intervalo aberto E contendo a tal que
f(b)≤ f(x), qualquer que seja o x ∈ E ∩ D
Definição : Aos valores do domínio a que correspondem os máximos / mínimos relativos da
função chamam-se maximizantes / minimizantes
Voltar

21. Funções
Noções gerais de uma função
• Injectividade de uma função
FDefinição : Uma função f é
injectiva num intervalo E⊂Df se
para dois valores quaisquer de E,
x1 e x2, se x1 ≠ x2 então f(x1) ≠
f(x2).
Definição : Uma função f é não
injectiva num intervalo E⊂Df se
existem pelo menos dois
objectos distintos com a mesma
imagem.
Voltar

22. Funções
Noções gerais de uma função
• Injectividade de uma função
Graficamente
Vê-se que uma função é não injectiva se existir pelo menos uma recta
horizontal que intersecte o gráfico da função em mais do que um ponto.
f é função injectiva f é função não injectiva

23. Funções
Noções gerais de uma função
• Sobrejectividade de uma função
FDefinição : Uma função g é
sobrejectiva se o seu
contradomínio coincide com o
conjunto de chegada.
g é sobrejectiva
f é não sobrejectiva