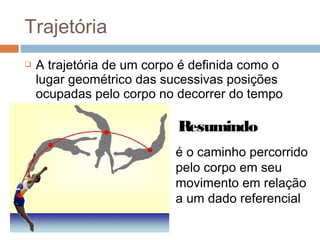
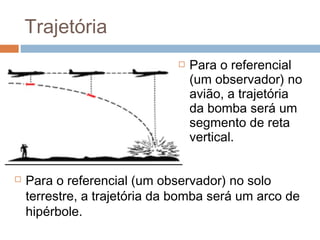
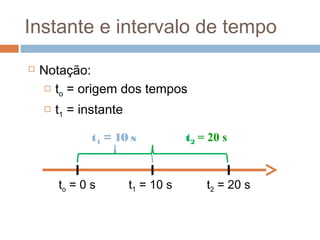
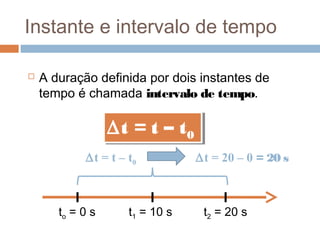
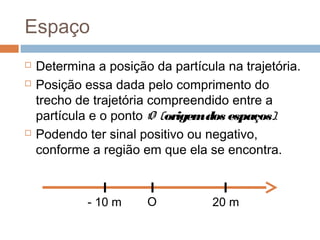
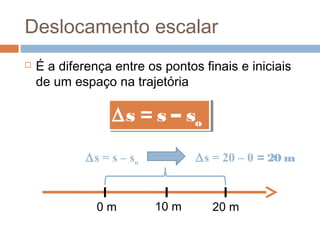
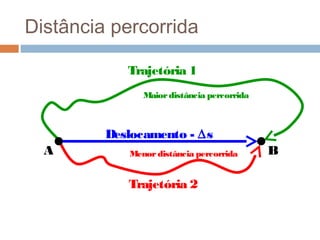
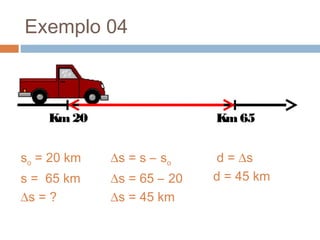
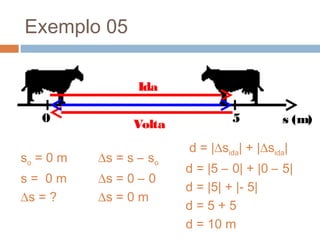
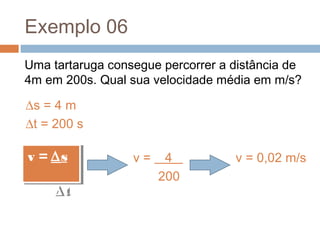
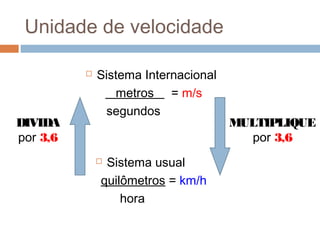
O documento discute conceitos básicos de cinemática, incluindo: (1) movimento e repouso definidos em relação à variação da posição de um corpo em relação a um referencial com o tempo; (2) deslocamento e distância percorrida; e (3) velocidade média calculada pela razão entre deslocamento e intervalo de tempo. Exemplos ilustram como calcular essas grandezas cinemáticas.

1. CINEMÁTICA
Introdução

2. Cinemática
 Parte da Física que estuda o movimento sem
preocupar-se com as causas que deram
origem ou interferem no movimento.

3. Ponto material ou partícula
 Dizemos que um corpo é
uma partícula quando suas
dimensões são muito
pequenas em comparação
com as demais dimensões
que participam do
fenômeno.

4. Corpo extenso
 É quando suas dimensões não são pequenas
em comparação com as demais dimensões que
participam do fenômeno.

5. O que é movimento?
Movimento é quando a posição entre o corpo e
o referencial variar com o tempo.
 Note que o passageiro no interiordo ônibus está em
movimento em relação ao observadorfixo na Terra,
porque sua posição muda com o decorrerdo tempo.

6. E repouso?
Repouso é quando a posição entre o corpo e o
referencial não variar no decorrer do tempo.
 Note que o passageiro no interiordo ônibus está em
repouso emrelação ao ônibus e ao motorista, porque a
sua posição emrelação a eles é sempre a mesma.

7. Exemplo 01
Enquanto o professor escreve na lousa:
a) o giz está em repouso ou em movimento em
relação á lousa? Justifique.
Enquanto o professor está escrevendo, o giz
muda de posição em relação à lousa, estando,
portanto, e m m o vim e nto em relação a ela.

8. Exemplo 01
b) a lousa está em repouso ou em movimento
em relação ao chão? Justifique.
A lousa não muda de posição em relação ao
chão, estando, portanto, e m re po uso em relação
a ele.

9. Exemplo 01
c) a lousa está em repouso ou em movimento
em relação ao giz? Justifique.
Os conceitos de movimento e de repouso são
simétricos, isto é, se um corpo está em
movimento (ou repouso) em relação a outro,
esta também está em movimento (ou repouso)
em relação ao primeiro. Assim, a lousa está em
movimento em relação ao giz. De fato, se
houver um inseto pousado no giz, por exemplo,
o inseto verá a lousa passando por ele.

10. Você sabe o que é trajetória?

11.  A trajetória de um corpo é definida como o
lugar geométrico das sucessivas posições
ocupadas pelo corpo no decorrer do tempo
é o caminho percorrido
pelo corpo em seu
movimento em relação
a um dado referencial
Resumindo
Trajetória

12.  Para o referencial
(um observador) no
avião, a trajetória
da bomba será um
segmento de reta
vertical.
 Para o referencial (um observador) no solo
terrestre, a trajetória da bomba será um arco de
hipérbole.
Trajetória

13. Trajetória

14. Instante e intervalo de tempo
 Notação:
 to = origem dos tempos
 t1 = instante
to = 0 s t1 = 10 s t2 = 20 s
t1 = 10 s t2 = 20 s

15. Instante e intervalo de tempo
 A duração definida por dois instantes de
tempo é chamada intervalo de tempo.
to = 0 s t1 = 10 s
∆t = t – t0
∆t = t – t0
t2 = 20 s
∆t = t – t0 ∆t = 20 – 0 = 20 s

16. Unidade de tempo
Nome Símbolo
segundo s
minuto min
hora h
1 h = 60 min
1 min = 60 s
1 h = 3600 s
 A unidade de tempo no Sistema Internacional
– SI – é o SEGUNDO.

17. Espaço
 Determina a posição da partícula na trajetória.
 Posição essa dada pelo comprimento do
trecho de trajetória compreendido entre a
partícula e o ponto O (origemdos espaços).
 Podendo ter sinal positivo ou negativo,
conforme a região em que ela se encontra.
- 10 m O 20 m

18. Deslocamento escalar
 É a diferença entre os pontos finais e iniciais
de um espaço na trajetória
∆s = s – so
∆s = s – so
0 m 10 m 20 m
∆s = s – so ∆s = 20 – 0 = 20 m

19. Exemplo 02
Um homem fez uma caminhada partindo do
marco 10km e chegando ao marco 50km. Qual
é a variação de espaço que o homem
percorreu?
∆s = s – so
Assim:
so = 10 km
s = 50 km
∆s = 50 – 10
∆s = 40 km
Então, o homem percorreu durante
a caminhada 40km sendo este
valor a variação de espaço ∆S.

20. Exemplo 03
O Bob esponja dos desenhos animados sabia
que o Patrique estava a 50km de distancia, Bob
Esponja quer saber qual é sua posição inicial se
o Patrique esta sobre o marco 50km.
∆s = s – so
Assim:
so = ?
∆s = 50 km
s = 50 km
50 = 50 – so
so = 50 – 50
so = 0 km
A posição inicial do Bob
Esponja é o 0 km.

21. Distância percorrida
 É a grandeza que informa quanto à partícula
efetivamente percorreu entre dois instantes.
 Calculada sempre em valor absoluto.
 A distância percorrida seguindo diferentes
trajetórias é habitualmente diferente, no
entanto, o deslocamento efetuado é sempre o
mesmo.

22. Distância percorrida
A B
Trajetória 1
Trajetória 2
Maiordistância percorrida
Menordistância percorrida
Deslocamento - ∆s

23. Exemplo 04
Um automóvel deslocou-se do km 20 até o km 65
de uma rodovia, sempre no mesmo sentido.
Determine o deslocamento e a distância
percorrida pelo automóvel.
Neste caso em que a partícula desloca-se
sempre em um mesmo sentido, a distância
percorrida será igual ao deslocamento
d = ∆sd = ∆s

24. Exemplo 04
Km 20 Km 65
so = 20 km
s = 65 km
∆s = ?
∆s = s – so
∆s = 65 – 20
∆s = 45 km
d = ∆s
d = 45 km

25. Exemplo 05
Um boi sai da posição zero da estrada, vai até a
posição 5m e depois retorna para a posição zero.
Qual foi o seu deslocamento? E a sua distância
percorrida?
Neste caso em que a partícula inverte o
sentido do movimento, a distância percorrida
será igual ao deslocamento da ida mais o
deslocamento da volta, em módulo.
d = |∆sida|+ |∆svolta|d = |∆sida|+ |∆svolta|

26. Exemplo 05
0 5
so = 0 m
s = 0 m
∆s = ?
∆s = s – so
∆s = 0 – 0
∆s = 0 m
d = |∆sida| + |∆sida|
d = |5 – 0| + |0 – 5|
d = |5| + |- 5|
d = 5 + 5
d = 10 m
s (m)
Ida
Volta

27. Unidade de distância
Nome Símbolo
quilômetro km
metro m
centímetro cm
milímetro mm
1 km = 1 000 m
1 m = 100 cm
1 cm = 10 mm
 A unidade de distância no Sistema Internacional
– SI – é o METRO.

28. Velocidade Média (VM)
onde:
ΔS = variação da posição
So = posição inicial
S = posição final
Δt = variação do tempo
to = instante inicial
t = instante final

29. Exemplo 06
Uma tartaruga consegue percorrer a distância de
4m em 200s. Qual sua velocidade média em m/s?
∆s = 4 m
∆t = 200 s
v = ∆s
∆t
v = ∆s
∆t
v = 4 .
200
v = 0,02 m/s

30. Unidade de velocidade
 Sistema Internacional
metros = m/s
segundos
 Sistema usual
quilômetros = km/h
hora
MULTIPLIQUE
por 3,6
DIVIDA
por 3,6

31. Exemplo 07
Faça as seguintes conversões:
a) 10 m/s em km/h
b) 108 km/h em m/s
10 x 3,6 = 36 km/h
Assim 10 m/s é
equivalente a 36 km/h
108 ÷ 3,6 = 30 m/s
Assim 108 km/h é
equivalente a 30 m/s

32. Acesse o blog e divirta!!!