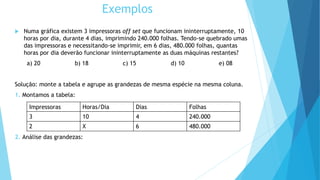
A regra de três é uma ferramenta para resolver questões envolvendo grandezas proporcionais, sendo dividida em simples e composta. A simples é usada para três valores, enquanto a composta se aplica a mais de três. O documento fornece exemplos práticos de como aplicar essas regras em situações reais.

1. Regra de Três: Simples e
Composta
Veja nesta aula um passo a passo sobre como resolver a regra de três
simples e composta

2. O que é regra de três?
 Regra de três é um processo para resolver problemas e/ou questões em que
envolvam propriedades diretamente ou inversamente proporcionais.
Mas Qual a diferença entre regra de três simples e composta?
 Regra de três Simples: Utilizamos quando temos três valores e um valor
desconhecido a ser encontrado.
 Regra de três Composta: Utilizamos quando temos mais de três valores e um
valor desconhecido a ser encontrado.
O que são grandezas diretamente ou inversamente proporcionais?
 Diretamente proporcional: Se aumentarmos uma grandeza a outra também
aumenta, na mesma proporção;
 Inversamente proporcional: Se aumentarmos uma grandeza a outra diminui, na
mesma proporção.

3. Regra de Três Simples
Para a resolução da regra de três simples, vamos realizar apenas 4 passos:
1. Crie uma tabela e agrupe as grandezas de mesma espécie na mesma coluna;
2. Verifique se são grandezas inversamente ou diretamente proporcionais;
3. Se as grandezas forem diretamente proporcionais, multiplicamos os fatores
cruzados, ou seja, multiplicamos em X. Se as grandezas forem inversamente
proporcionais, multiplicamos direto.
4. Resolver a questão.

4. Exemplos
 Para se construir um muro de 17m² são necessários 3 trabalhadores. Quantos
trabalhadores serão necessários para construir um muro de 51m²?
a) 6 b) 8 c) 9 d) 10 e) 12
Solução:
1. Montamos a tabela:
2. Verificar se são diretas ou inversas:
Se aumentarmos a área de construção, precisamos aumentar o número de
trabalhadores para construirmos o muro no mesmo período.
Logo, são diretamente proporcionais!
Área (m²) Nº de Trabalhadores
17 3
51 X

5. 3. Como são diretamente proporcionais, multiplicamos em X:
17 3
51 X
4. Resolução:
17 * X = 51 * 3
17 * X = 153
X =
153
17
X = 9
Portanto, serão 9 trabalhadores para a construção de um muro de 51 m².
Letra C

6.  Um automóvel com velocidade de 80 km/h gasta 15 minutos em certo percurso. Se
a velocidade for reduzida para 60 km/h, que tempo, em minutos, será gasto no
mesmo percurso?
a) 10 b) 12 c) 18 d) 20 e) 24
Solução:
1. Montamos a tabela:
2. Verificar se são diretas ou inversas:
Se diminuirmos a velocidade, demoraremos mais tempo para percorrer o percurso, ou
seja, se diminuirmos a velocidade, aumentamos o tempo.
Logo, são inversamente proporcionais!
Velocidade (km/h) Tempo (min)
80 15
60 X

7. 3. Como são inversamente proporcionais, multiplicamos direto:
80 15
60 X
4. Resolução:
80 * 15 = 60 * X
1200 = 60 * X
X =
1200
60
X = 20
Portanto, se diminuirmos a velocidade de 80 km/h para 60 km/h, o tempo de
viagem aumentará de 15 minutos para 20 minutos.
Letra D

8. Regra de Três Composta
Para a resolução da regra de três composta, analisamos cada grandeza
relativamente à grandeza onde está o X. Assim, para resolver regra de três
composta você deve reduzir o problema em várias regra de três simples.
Veja os Exemplos nos slides a seguir

9.  Numa gráfica existem 3 impressoras off set que funcionam ininterruptamente, 10
horas por dia, durante 4 dias, imprimindo 240.000 folhas. Tendo-se quebrado umas
das impressoras e necessitando-se imprimir, em 6 dias, 480.000 folhas, quantas
horas por dia deverão funcionar ininterruptamente as duas máquinas restantes?
a) 20 b) 18 c) 15 d) 10 e) 08
Solução: monte a tabela e agrupe as grandezas de mesma espécie na mesma coluna.
1. Montamos a tabela:
2. Análise das grandezas:
Impressoras Horas/Dia Dias Folhas
3 10 4 240.000
2 X 6 480.000
Exemplos

10.  Inicialmente, coloquemos uma seta orientada no sentido contrário do X, isto é, para
cima. Vamos analisar a outra parte.
10
X
1º Caso = Comparação com número de impressoras
Inversa: se diminuímos o número de impressoras, precisamos aumentar a carga horária de
trabalho. Assim, coloquemos uma seta contrária, isto é, para baixo.
3 10
2 x
2º Caso = Comparação com dias
Inversa: se aumentamos o número de dias de trabalho, podemos diminuir a carga horária
de trabalho. Assim, também coloquemos uma seta contrária, isto é, para baixo.
4 10
6 X

11. 3º Caso = Comparação com número de Folhas impressas
Direta: se aumentamos a quantidade de trabalho a ser feito, precisamos aumentar a carga
horária de trabalho. Então, neste caso, coloquemos uma seta na mesma direção do X, isto é,
para cima.
240.000 10
480.000 x
Juntando tudo, temos:
3 10 4 240.000
2 X 6 480.000
Então, sempre respeitando o sentido das setas, ou seja, quando for inversa (seta vermelha)
invertemos os valores (denominador, parte de baixo, vai para o numerador, parte de cima) e
quando for direta deixa como está.
2 10 6 240.000
3 X 4 480.000

12.  Agora, para resolver, vamos isolar a grandeza que possui o X, para formarmos
a equação. Veja:
10 2 6 240.000
X 3 4 480.000
Como pode ver, o que está antes da igualdade multiplicamos em X; o que está
depois da igualdade multiplicamos em linha. Assim, temos a seguinte equação:
10
𝑥
=
2
3
∗
6
4
∗
240.000
480.000
10
𝑋
=
2.880.000
5.760.000
57.600.000 = 2.880.000 * X
𝑋 =
57.600.000
2.880.000
= 20
Logo, as máquinas restantes devem funcionar 20 horas/dia para
produzir 480.000 folhas em 6 dias. Resposta: A

13.  24 operários fazem 2/5 (dois quinto) de determinado serviço em 10 dias,
trabalhando 7 horas por dia. Em quantos dias a obra estará terminada,
sabendo-se que foram dispensados 4 operários e o regime de trabalho
diminuído de uma hora por dia?
a) 08 b) 11 c) 12 d) 21 e) 18
Solução: monte a tabela e agrupe as grandezas de mesma espécie na mesma
coluna.
1. Montamos a tabela:
2. Análise das grandezas:
Operários Partes do Trabalho Dias Horas/Dias
24 2 10 7
20 3 X 6

14.  Inicialmente, coloquemos uma seta orientada no sentido contrário do X, isto é, para
cima. Vamos analisar a outra parte.
10
X
1º Caso = Comparação com número de Operários
Inversa: diminuindo o número de operários a quantidade de dias aumenta.
24 10
20 x
2º Caso = Comparação com partes do Trabalho
Direta: aumentando o trabalho a quantidade de dias aumenta.
2 10
3 X

15. 3º Caso = Comparação com a quantidade de horas/dia
Inversa: diminuindo a jornada diária a quantidade de dias aumenta.
7 10
6 x
Juntando tudo, temos:
24 2 10 7
20 3 X 6
Então, sempre respeitando o sentido das setas, ou seja, quando for inversa (seta vermelha)
invertemos os valores (denominador, parte de baixo, vai para o numerador, parte de cima) e
quando for direta deixa como está.
20 2 10 6
24 3 X 7

16.  Agora, para resolver, vamos isolar a grandeza que possui o X, para formarmos
a equação. Veja:
10 2 20 6
X 3 24 7
Como pode ver, o que está antes da igualdade multiplicamos em X; o que está
depois da igualdade multiplicamos em linha. Assim, temos a seguinte equação:
10
𝑥
=
2
3
∗
20
24
∗
6
7
10
𝑋
=
240
504
240 * X = 5.040
𝑋 =
5.040
240
= 21
Logo, a obra será terminada em 21 dias com 20 operários trabalhando 6
horas/dia. Resposta: D