1) O documento discute conceitos estatísticos como distribuição normal, uniforme e probabilidades. 2) A distribuição normal é descrita como uma das mais importantes e amplamente usadas em pesquisas, com média e desvio padrão como parâmetros. 3) Exemplos ilustram como calcular probabilidades usando a distribuição normal reduzida e tabelas Z.

1. CURSO DE ESTATÍSTICA I
Ricardo Bruno N. dos Santos
FACECON-PPGE (UFPA)

2. Distribuição Normal

3. DISTRIBUIÇÕES CONTÍNUAS
Dentre as várias distribuições de probabilidade contínuas,
abordaremos aqui apenas a distribuição normal, pois ela apresenta
grande aplicação em pesquisas científicas e tecnológicas. Grande
parte das variáveis contínuas de interesse prático segue essa
distribuição, aliada ao Teorema do Limite Central (TLC), que é a base
das estimativas e dos testes de hipóteses realizados sobre a média
de uma população qualquer, e garante que a distribuição amostral
das médias segue uma distribuição normal, independentemente da
distribuição da variável em estudo, como será visto mais adiante.

4. DISTRIBUIÇÕES CONTÍNUAS
Mas antes de entrarmos na distribuição normal é bom entender o
conceito de distribuição uniforme. A distribuição uniforme é a
distribuição de probabilidades contínua mais simples de conceituar:
a probabilidade de se gerar qualquer ponto em um intervalo contido
no espaço amostral é proporcional ao tamanho do intervalo.
Outra maneira de se dizer "distribuição uniforme" seria "um
número finito de resultados com chances iguais de acontecer".
Um simples exemplo de distribuição uniforme é lançar um dado
não viciado. Os possíveis valores são 1,2,3,4,5,6, e a cada turno que
o dado é jogado a probabilidade de cada valor é 1/6. Se dois dados
são lançados e seus valores adicionados, a distribuição resultante
não é mais uniforme pois as somas não são uma variável
equiprovável.

5. DISTRIBUIÇÕES CONTÍNUAS
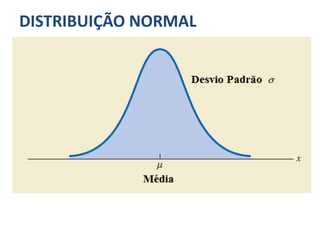
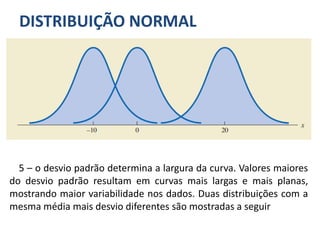
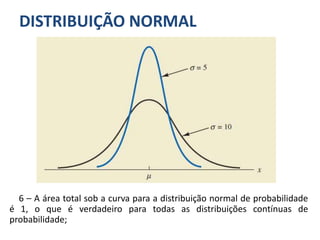
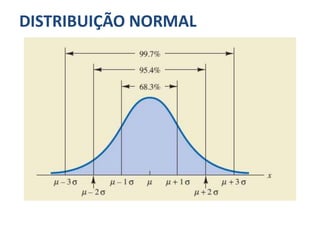
A distribuição discreta uniforme em si não possui parâmetros. No
entanto, é conveniente representar seus possíveis resultados com
um intervalo fechado [a,b], sendo 'a' e 'b' considerados os principais
parâmetros da distribuição. Com isso a função acumulada dessa
distribuição é representada como
𝐹 𝑘; 𝑎, 𝑏 =
𝑘 −𝑎+1
𝑏−𝑎+1
Ou
𝑓 𝑥; 𝑎, 𝑏 =
1
𝑏 − 𝑎
0
, 𝑎 ≤ 𝑥 ≤ 𝑏

6. DISTRIBUIÇÕES CONTÍNUAS
Exemplo: Num teste intelectual com alunos de um colégio Y, o
tempo para realização de uma bateria de questões de raciocínio
lógico é medido e anotado para ser comparado com um modelo
teórico. Este teste é utilizado para identificar o desenvolvimento da
capacidade de raciocínio lógico e auxiliar a aplicação de medidas
corretivas. O modelo teórico considera T, tempo de teste em
minutos, como uma variável aleatória contínua com função de
densidade de probabilidade dada por:











contráriocaso
tse
tset
tf
0
1510
20
3
;108)4(
40
1
)(

7. DISTRIBUIÇÕES CONTÍNUAS
O gráfico da fdp é apresentado a seguir (construiremos ele no
software R). Deve ser notado que, pela definição de f(x), ela se
anula para t < 8 ou t >15.
Vamos verificar agora se a função f(t) satisfaz a definição de
densidade. Para calcular P(9 < T  12), vamos obter a área sob f(t) no
intervalo (9; 12]:

8. DISTRIBUIÇÕES CONTÍNUAS
Assim P(9< T  12) = 7/16 valor esse obtido pela soma do trapézio
definido no intervalo (9, 10) com o retângulo determinado pelo
intervalo [10,12] (veja a figura).
6 8 10 12 14 16 18
0.000.050.100.15
t
f(t)

9. DISTRIBUIÇÕES CONTÍNUAS
Através do uso de integral, essa mesma probabilidade seria
calculada da seguinte forma:
12 10 12
9 9 10
10 122
10 12
9 10
109
(9 12) ( ) ( ) ( )
1 3 1 3
( 4) 4
40 20 40 2 20
11 6 7
0,4375
80 20 16
P T f t dt f t dt f t dt
t
t dt dt t t
     
   
        
  
  
  
 

10. DISTRIBUIÇÃO NORMAL
A distribuição normal é uma das mais essenciais e importantes
distribuições da estatística, conhecida também como Distribuição de
Gauss ou Gaussiana. Foi primeiramente introduzida pelo matemático
Abraham de Moivre.
Além de descrever uma série de fenômenos físicos e financeiros,
possui grande uso na estatística inferencial. É inteiramente descrita
por seus parâmetros de média e desvio padrão, ou seja,
conhecendo-se estes consegue-se determinar qualquer
probabilidade em uma distribuição Normal.

11. DISTRIBUIÇÃO NORMAL
Um interessante uso da Distribuição Normal é que ela serve de
aproximação para o cálculo de outras distribuições quando o
número de observações fica grande. Essa importante propriedade
provém do Teorema do Limite Central que diz que "toda soma de
variáveis aleatórias independentes de média finita e variância
limitada é aproximadamente Normal, desde que o número de
termos da soma seja suficientemente grande" (Ou seja, que a
amostra seja maior que 30 observações).

12. TEOREMA DO LIMITE CENTRAL

13. DISTRIBUIÇÃO NORMAL
A função densidade de probabilidade da distribuição normal
é dada por:
𝒇 𝒙 =
𝟏
𝟐𝝅𝝈 𝟐
𝒆𝒙𝒑 −
𝟏
𝟐
𝒙 − 𝝁
𝝈
𝟐
, 𝑥 ∈ (−∞; ∞)
Onde:
 e  são a média e o desvio padrão, respectivamente, da
distribuição de probabilidade.
𝜋 corresponde a 3,1415 e exp a uma função exponencial.

14. DISTRIBUIÇÃO NORMAL
A variação natural de muitos processos industriais é realmente
aleatória. Embora as distribuições de muitos processos possam
assumir uma variedade de formas, muitas variáveis observadas
possuem uma distribuição de frequências que é, aproximadamente,
uma distribuição de probabilidade Normal.
Probabilidade é a chance real de ocorrer um determinado evento,
isto é, a chance de ocorrer uma medida em um determinado
intervalo. Por exemplo, a frequência relativa deste intervalo,
observada à partir de uma amostra de medidas, é a aproximação da
probabilidade. E a distribuição de frequências é a aproximação da
distribuição de probabilidades.
A distribuição é normal quando tem a forma de "sino":

15. DISTRIBUIÇÃO NORMAL

16. DISTRIBUIÇÃO NORMAL
Algumas características da distribuição normal:
1 – Há uma família inteira de distribuições normais de
probabilidade. Elas são diferenciadas por suas médias () e desvios-
padrões ();
2 – O ponto mais alto na curva normal está na média, que também
é a mediana e a moda da distribuição;
3 – A média da distribuição pode ser qualquer valor numérico:
negativo, zero ou positivo. No próximo gráfico temos três curvas
normais com o mesmo desvio padrão mas três diferentes médias (-
10; 0; e 20);
4 – A distribuição normal de probabilidade é simétrica, em que a
forma da curva à esquerda da média é uma imagem espelhada da
forma da curva à direita da média. Os extremos da curva estendem-
se ao infinito em ambas as direções e teoricamente nunca tocam o
eixo horizontal.

17. DISTRIBUIÇÃO NORMAL
5 – o desvio padrão determina a largura da curva. Valores maiores
do desvio padrão resultam em curvas mais largas e mais planas,
mostrando maior variabilidade nos dados. Duas distribuições com a
mesma média mais desvio diferentes são mostradas a seguir

18. DISTRIBUIÇÃO NORMAL
6 – A área total sob a curva para a distribuição normal de probabilidade
é 1, o que é verdadeiro para todas as distribuições contínuas de
probabilidade;

19. DISTRIBUIÇÃO NORMAL
7 – As probabilidades para a variável aleatória normal são dadas
por áreas sob a curva. A porcentagem de valores em alguns
intervalos comumente usados são:
a) 68,26% dos valores de uma variável aleatória normal estão
dentro de um desvio padrão positivou ou negativo de sua média;
b) 95,44% dos valores de uma variável aleatória normal estão
dentro de dois desvios padrões positivos ou negativos de sua
média;
c) 99,72% dos valores de uma variável aleatória normal estão
dentro de três desvios padrões positivos ou negativos de sua
média

20. DISTRIBUIÇÃO NORMAL

21. DISTRIBUIÇÃO NORMAL
Portanto, a área sob a curva entre os pontos a e b, em que a < b,
representa a probabilidade da variável X assumir um valor entre a e
b (área escura), como observamos a seguir.
𝑷(𝒂 ≤ 𝒙 ≤ 𝒃)
𝑷(𝒙 < 𝒂)
𝑷(𝒙 > 𝒃)

22. DISTRIBUIÇÃO NORMAL
Desse modo, você pode associar que, no caso das distribuições
contínuas, a área do gráfico corresponde a probabilidades.
Então, veja a notação utilizada para a distribuição normal:
𝑿~𝑵(𝝁, 𝝈 𝟐)
Para calcularmos as probabilidades via distribuição normal, é
necessário o conhecimento de cálculo integral. Assim, procuramos
tabelar os valores de probabilidade que seriam obtidos por meio da
integração da função densidade de probabilidade normal em um
determinado intervalo.
A dificuldade para se processar esse tabelamento se prendeu na
infinidade de valores que  (média) e  (desvio padrão) poderiam
assumir. Nessas condições, teríamos que dispor de uma tabela para
cada uma das infinitas combinações de  e , ou seja, em cada
situação que se quisesse calcular uma probabilidade.

23. DISTRIBUIÇÃO NORMAL
Para facilitar esse problema, pode-se obter uma nova forma para a
distribuição normal, que não seja influenciada por  e . O problema
foi solucionado mediante emprego de uma nova variável definida
por:
𝒛 =
𝒙 − 𝝁
𝝈
Essa variável transforma todas as distribuições normais em uma
distribuição normal reduzida ou padronizada, de média zero e desvio
padrão um. Então, temos: 𝑍 ~ 𝑁(0,1).
Assim, utilizamos apenas uma tabela para o cálculo de
probabilidades para qualquer que seja a curva correspondente a
uma distribuição normal.
Portanto, para um valor de x =  em uma distribuição normal
qualquer, corresponde o valor:

24. DISTRIBUIÇÃO NORMAL
𝑧 =
𝑥−𝜇
𝜎
=
𝜇−𝜇
𝜎
= 0 na distribuição normal reduzida.
Para 𝑥 = 𝜇 + 𝜎, tem-se:
𝑧 =
𝑥−𝜇
𝜎
=
𝜇+𝜎−𝜇
𝜎
= 1

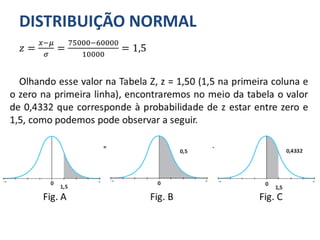
25. DISTRIBUIÇÃO NORMAL
Exemplo: Considere a arrecadação como um tributo de uma
pequena cidade. Verificamos que essa arrecadação seguia uma
distribuição normal com duração média de R$ 60.000,00 e desvio
padrão de R$ 10.000,00. Procuramos, então, responder os seguintes
questionamentos:
a) Qual a probabilidade de uma arrecadação ser maior do que R$
75.000,00?
Como a variável arrecadação apresenta distribuição
aproximadamente normal com média 60000 e variância de 100002
[𝑋~ 𝑁(60000; 100002)] e procura-se calcular a
𝑃(𝑋 > 75000) = ?
Primeiramente, precisamos transformar a variável 𝑋 em 𝑍 e,
depois, substituindo na expressão, teremos:

26. DISTRIBUIÇÃO NORMAL
𝑧 =
𝑥−𝜇
𝜎
=
75000−60000
10000
= 1,5
Olhando esse valor na Tabela Z, z = 1,50 (1,5 na primeira coluna e
o zero na primeira linha), encontraremos no meio da tabela o valor
de 0,4332 que corresponde à probabilidade de z estar entre zero e
1,5, como podemos pode observar a seguir.
Fig. A Fig. B Fig. C

27. DISTRIBUIÇÃO NORMAL
A área escura da figura corresponde a P(X>75000), que é a mesma
coisa que: P(z > 1,50). Então:
𝑃 𝑧 > 1,5 𝐹𝑖𝑔. 𝐴 =
= 𝑃 0 < 𝑧 < ∞ 𝐹𝑖𝑔. 𝐵 − 𝑃 0 < 𝑧 < 1,50 𝐹𝑖𝑔. 𝐶
= 0,5 − 0,4332
= 0,0668
Retirou-se a probabilidade encontrada de 0,5, pois esse valor
corresponde à probabilidade de zero até o infinito.

28. DISTRIBUIÇÃO NORMAL
b) Qual a probabilidade da arrecadação estar entre R$ 50.000,00 e
R$ 70.000,00?
𝑃 50000 < 𝑋 < 70000 =?
Primeiramente, precisamos transformar a variável 𝑋 em 𝑍 e,
depois, substituindo na expressão de 𝑍, teremos valores de 𝑍1 e 𝑍2,
relacionados aos valores de 𝑋1 = 50000 e 𝑋2 = 70000:
𝑧1 =
𝑥1−𝜇
𝜎
=
50000−60000
10000
= −1
𝑧2 =
𝑥2−𝜇
𝜎
=
70000−60000
10000
= 1

29. DISTRIBUIÇÃO NORMAL
Pode-se verificar que:
𝑃 50000 < 𝑋 < 70000 = 𝑃 −1 < 𝑧 < 1 = 0,3413 + 0,3413
= 0,6826

30. DISTRIBUIÇÃO NORMAL
c) Qual a probabilidade da arrecadação estar entre R$ 63.000,00 e
R$ 70.000,00?
𝑃(63000 < 𝑋 < 70000) = ?
𝑧1 =
63000−60000
10000
= 0,30
𝑧2 =
70000−60000
10000
= 1

31. DISTRIBUIÇÃO NORMAL
𝑃 63000 < 𝑋 < 70000 = 𝑃 0,30 < 𝑧 < 1,00
= 0,3413 − 0,1179
= 0,2234
Observe que existem outras distribuições tanto discretas quanto
contínuas que não foram abordadas neste livro. Portanto,
recomendamos que você procure outras fontes de conhecimento, a
começar por fazer uma pesquisa na internet sobre essas
distribuições.