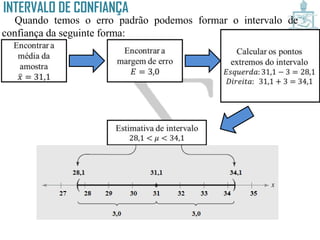
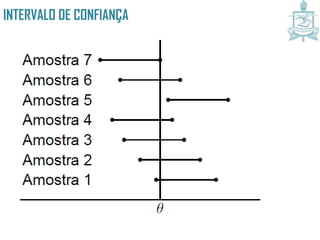
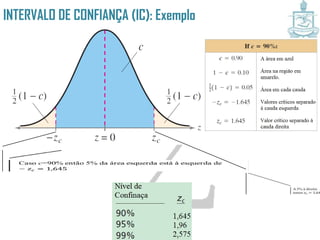
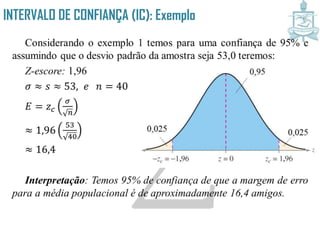
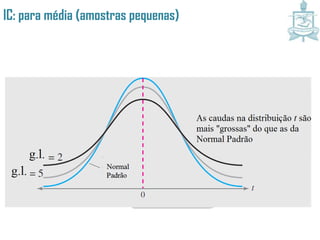
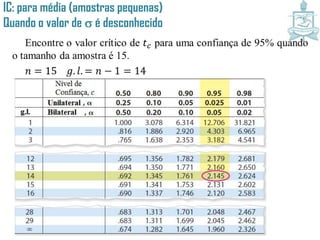
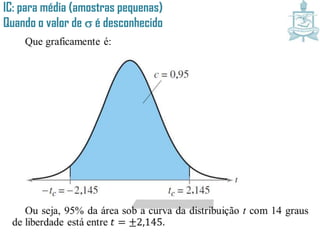
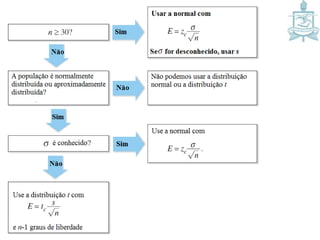
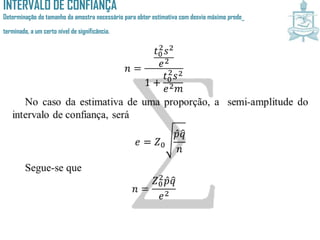
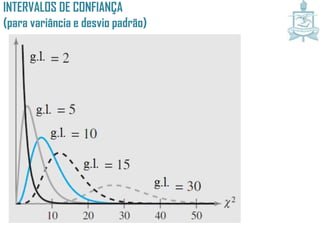
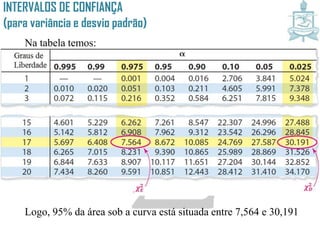
Este documento discute intervalos de confiança, que fornecem uma faixa de valores dentro da qual o parâmetro populacional verdadeiro tem uma certa probabilidade de estar localizado. Intervalos de confiança são construídos usando dados amostrais e fornecem uma estimativa do erro na estimativa pontual de um parâmetro. O documento também discute como calcular intervalos de confiança para a média populacional e proporção populacional usando estatística inferencial.

1. Estatística II
UNIVERSIDADE FEDERAL DO PARÁ
INSTITUTO DE CIÊNCIAS SOCIAIS APLICADAS
FACULDADE DE ECONOMIA
Prof. Dr. Ricardo Bruno Nascimento dos Santos

2. INTERVALO DE CONFIANÇA

3. INTERVALO DE CONFIANÇA
É a partir deste tópico que iremos dar início a estatística
inferencial.
Um exemplo, seria com o valor da média amostral de uma linha
de produção de carros de um certo fabricante de automóveis, o órgão
de regulação pode estimar o índice médio de economia de
combustível como sendo 31,1 milhas por galão para toda linha de
carros. Como essa estimativa representa um único número
representado por um ponto em uma linha de números, ele é chamado
de ESTIMATIVA PONTUAL. O problema de uma estimativa
pontual é que ela raramente se iguala ao parâmetro exato (média,
desvio padrão ou proporção) de uma população.

4. INTERVALO DE CONFIANÇA
Quando temos o erro padrão podemos formar o intervalo de
confiança da seguinte forma:

5. INTERVALO DE CONFIANÇA
Logo, a empresa pode estar 90% confiante de que o índice médio
de economia de combustível para toda linha de automóveis de
passeio está entre 28,1 e 34,1 milhas por galão.

6. INTERVALO DE CONFIANÇA
Antes de verificarmos a ideia intuitiva do que seja um intervalo de
confiança, vamos verificar alguns importantes conceitos no que
tange a estimação.
Estimar o consumo médio de um automóvel, estimar o tempo
médio que um funcionário leva a aprender uma nova tarefa ou
estimar a percentagem (proporção) de pessoas que irão consumir um
produto que vai ser lançado no mercado, são exemplos de estimação.
A estimação pode ser feita por dois processos:
• Estimação Pontual
• Estimação Intervalar

7. INTERVALO DE CONFIANÇA

8. INTERVALO DE CONFIANÇA

9. INTERVALO DE CONFIANÇA
A estimação intervalar (ou estimativa intervalar) consiste na
determinação de um intervalo onde, com uma certa confiança
(probabilidade), esteja o parâmetro θ desconhecido, tendo-se em
conta um seu estimador.
Assim, P(L1 < θ < L2) = significa que a probabilidade do
intervalo aleatório (L1, L2) conter o valor exato θ é .
O intervalo (L1, L2) é designado por INTERVALO DE
CONFIANÇA para o parâmetro θ, com um nível de confiança .
Depois de recolhida uma amostra aleatória, usam-se os valores
observados dessa amostra, para calcular os valores observados das
variáveis aleatórias L1 e L2, que se representam, respectivamente, por
l1 e l2.
(l1 e l2) é o intervalo de confiança concreto para aquela amostra.

10. INTERVALO DE CONFIANÇA

11. INTERVALO DE CONFIANÇA
Vantagem
É possível determinar o erro máximo cometido na estimação, com
uma certa confiança
Notas
Tem em conta as variações das estatísticas amostrais de amostra
para amostra.
Nunca podemos ter intervalos com 100% de confiança.

12. INTERVALO DE CONFIANÇA
Suponha que estejamos interessados num parâmetro populacional
verdadeiro (mas desconhecido) . Podemos estimar o parâmetro
usando informação de nossa amostra. Chamamos o único número
que representa o valor mais plausível do parâmetro (baseado nos
dados amostrais) de uma ESTIMATIVA PONTUAL de .
Contudo, sabemos que o valor estimado na maior parte das vezes não
será exatamente igual ao valor verdadeiro. Então, também seria
interessante encontrar um intervalo de confiança que forneça um
intervalo de valores plausíveis para o parâmetro baseado nos dados
amostrais.

13. INTERVALO DE CONFIANÇA (IC)
Portanto, um intervalo de confiança de 95% para um parâmetro
populacional fornece um intervalo no qual estaríamos 95%
confiantes de cobertura do verdadeiro valor do parâmetro.
Tecnicamente, 95% de todos os intervalos de confiança que
construirmos conterão o verdadeiro valor do parâmetro (dado que
todas as suposições envolvidas estejam corretas). Então se
obtivermos um intervalo de confiança para o parâmetro para cada
uma dentre 100 amostras aleatórias da população, somente 5, em
média destes intervalos de confiança não conterão .
Esses intervalos podem ser obtidos para: médias, diferença de
médias; proporções; diferenças em proporções; etc.
Os valores mais comuns de intervalos envolvem 90, 95 e 99% de
representatividade, porém, o mais comum é o cálculo de 95%.

14. INTERVALO DE CONFIANÇA (IC): Exemplo
No caso do Facebook, a probabilidade de que a média
populacional seja exatamente 130,8 é praticamente zero. Portanto,
em vez de estimarmos como sendo exatamente 130,8 usando uma
estimativa pontual, poderemos supor que está em um intervalo.
Tratar a média dentro de um intervalo é conhecido como
ESTIMATIVA INTERVALAR. Suponha que a margem de erro seja
15,7, então a estimativa intervalar fica como abaixo:

15. INTERVALO DE CONFIANÇA (IC): Exemplo

16. INTERVALO DE CONFIANÇA (IC): Exemplo

17. INTERVALO DE CONFIANÇA (IC)

18. INTERVALO DE CONFIANÇA (IC): Exemplo

19. INTERVALOS DE CONFIANÇA: Para média populacional

20. INTERVALOS DE CONFIANÇA: Para média populacional

21. INTERVALO DE CONFIANÇA: R
Pesquisar e fazer os intervalos de confiança no R.

22. INTERVALO DE CONFIANÇA
Quando o valor de é conhecido

23. INTERVALO DE CONFIANÇA
Quando o valor de é conhecido

24. INTERVALO DE CONFIANÇA
Quando o valor de é conhecido

25. INTERVALO DE CONFIANÇA
Quando o valor de é conhecido

26. IC: para média (amostras pequenas)

27. IC: para média (amostras pequenas)

28. IC: para média (amostras pequenas)

29. IC: para média (amostras pequenas)
Quando o valor de é desconhecido

30. IC: para média (amostras pequenas)
Quando o valor de é desconhecido

31. IC: para média (amostras pequenas)
Quando o valor de é desconhecido

32. IC: para média (amostras pequenas)
Quando o valor de é desconhecido

33. IC: para média (amostras pequenas)
Quando o valor de é desconhecido

34. IC: Qual distribuição usar?

35. INTERVALO DE CONFIANÇA
Intervalo de confiança para uma proporção

36. INTERVALO DE CONFIANÇA
Intervalo de confiança para uma proporção

37. INTERVALO DE CONFIANÇA
Intervalo de confiança para uma proporção

38. INTERVALO DE CONFIANÇA
Intervalo de confiança para uma proporção

40. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

41. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

42. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

43. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

44. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

45. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

46. INTERVALO DE CONFIANÇA
Determinação do tamanho da amostra necessário para obter estimativa com desvio máximo prede_
terminado, a um certo nível de significância.

47. INTERVALO DE CONFIANÇA
Prática
Agora veremos a prática no R
A vida média de baterias automotivas de uma certa marca está
sendo estudada. Baseado em estudos similares, com outras marcas, é
possível admitir que a vida dessas baterias segue a distribuição
Normal com desvio padrão de 4,5 meses. Foram colocadas 25
baterias da mesma marca em teste e foi registrado a vida média de
cada uma delas medido em meses conforme abaixo;
x
29.65, 23.34, 25.89, 23.20, 24.50, 24.73, 22.64, 14.05, 22.97, 22.04,
23.67, 25.07, 20.61, 19.50, 25.54, 26.71, 25.86, 24.20, 19.07, 20.86,
21.80, 25.48, 18.85, 17.69, 23.67

48. INTERVALO DE CONFIANÇA
Prática
Calcule o intervalo de confiança para coeficientes de confiança de
90%, 95% e 99%
.
25
5,4
645,122,8636;
25
5,4
645,122,8636%)90,(IC
.4805,122,8636;4805,122,8636%)90,(IC
.3441,24;3831,21%)90,(IC
.
25
5,4
96,122,8636;
25
5,4
96,122,8636%)95,(IC
.6276,24;0996,21%)95,(IC
.
25
5,4
575,222,8636;
25
5,4
575,222,8636%)99,(IC
.1811,25;5461,20%)99,(IC

49. INTERVALO DE CONFIANÇA
Prática
2
1,645 4,5
2 54,797 55
2
n

50. INTERVALO DE CONFIANÇA
Prática
Agora tratemos de um exemplo cujo desvio padrão seja
desconhecido.
Exemplo: Deseja-se achar o intervalo de confiança para a média
populacional do consumo de oxigênio em cm3/min do rim, quando
atacado por uma certa moléstia. Os valores medidos em cinco
pacientes com a moléstia foram: 14,4; 12,9; 15,0; 13,7; 13,5.
Considerando na tabela t o valor de erro para 10%, qual seria o
nosso intervalo de confiança?
No R teríamos

51. INTERVALOS DE CONFIANÇA
(para variância e desvio padrão)

52. INTERVALOS DE CONFIANÇA
(para variância e desvio padrão)

53. INTERVALOS DE CONFIANÇA
(para variância e desvio padrão)

54. INTERVALOS DE CONFIANÇA
(para variância e desvio padrão)
Na tabela temos:
Logo, 95% da área sob a curva está situada entre 7,564 e 30,191

55. PRÓXIMA AULA
TESTES DE HIPÓTESE