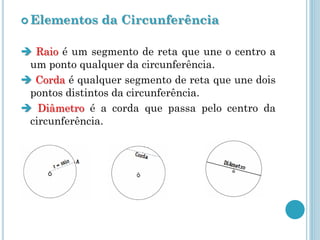
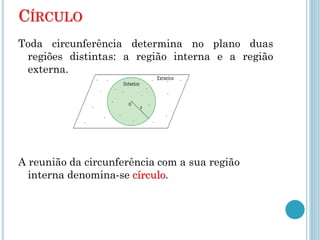
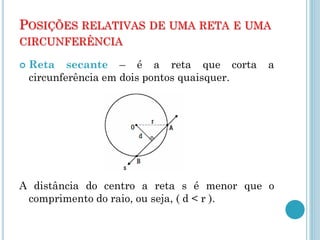
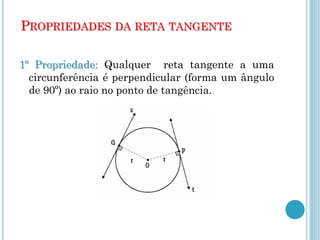
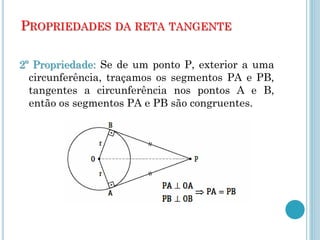
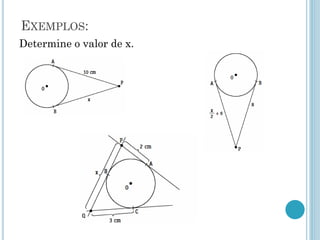
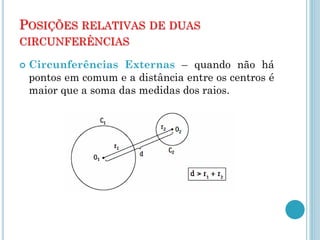
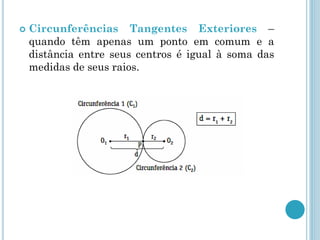
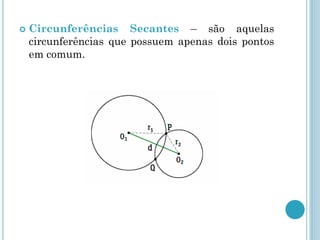
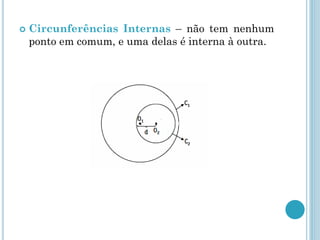
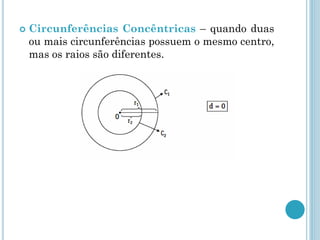
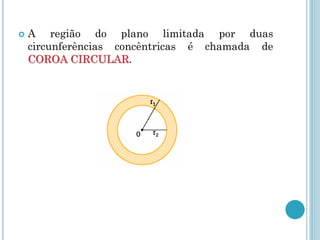
Este documento descreve os elementos básicos da circunferência e suas propriedades, incluindo raio, diâmetro, corda e centro. Também discute as posições relativas de uma reta e duas circunferências, como secante, tangente e externa. Finalmente, define os tipos de posições que duas circunferências podem ter, como externas, tangentes ou secantes.

1. A
CIRCUNFERÊNCIA
Profª - Rosemary e Tatiane

2. Circunferência é a figura geométrica formada por
todos os pontos de um plano que distam
igualmente de um ponto fixo desse plano.
Esse ponto fixo é chamado de centro da
circunferência (ponto O).

3.  Elementos da Circunferência
 Raio é um segmento de reta que une o centro a
um ponto qualquer da circunferência.
 Corda é qualquer segmento de reta que une dois
pontos distintos da circunferência.
 Diâmetro é a corda que passa pelo centro da
circunferência.

4. Uma relação importante que podemos notar é que a
medida do diâmetro (d) é igual ao dobro da
medida do raio ( r ), ou seja, diâmetro = 2r.
Exemplos:
1) De acordo com a figura que nome recebem os
segmentos?

5. 2) Dada uma circunferência de centro O e raio 6
cm, determine a medida do diâmetro.
3) Dada uma circunferência de centro O e diâmetro
de 20 cm, determine a medida do raio.

6. CÍRCULO
Toda circunferência determina no plano duas
regiões distintas: a região interna e a região
externa.
A reunião da circunferência com a sua região
interna denomina-se círculo.

7. POSIÇÕES RELATIVAS DE UMA RETA E UMA
CIRCUNFERÊNCIA
 Reta secante – é a reta que corta a
circunferência em dois pontos quaisquer.
A distância do centro a reta s é menor que o
comprimento do raio, ou seja, ( d < r ).

8.  Reta tangente – é a reta que toca a
circunferência em um único ponto (P). Esse ponto
é conhecido como ponto de tangência ou de
contato.
A distância do centro a reta t é igual ao
comprimento do raio, ou seja, ( d = r ).

9.  Reta externa – não há nenhum ponto em
comum com a circunferência.
A distância do centro a reta s é maior que o
comprimento do raio, ou seja, ( d > r ).

10. PROPRIEDADES DA RETA TANGENTE
1º Propriedade: Qualquer reta tangente a uma
circunferência é perpendicular (forma um ângulo
de 90º) ao raio no ponto de tangência.

11. PROPRIEDADES DA RETA TANGENTE
2º Propriedade: Se de um ponto P, exterior a uma
circunferência, traçamos os segmentos PA e PB,
tangentes a circunferência nos pontos A e B,
então os segmentos PA e PB são congruentes.

12. EXEMPLOS:
Determine o valor de x.

13. POSIÇÕES RELATIVAS DE DUAS
CIRCUNFERÊNCIAS
 Circunferências Externas – quando não há
pontos em comum e a distância entre os centros é
maior que a soma das medidas dos raios.

14.  Circunferências Tangentes Exteriores –
quando têm apenas um ponto em comum e a
distância entre seus centros é igual à soma das
medidas de seus raios.

15.  Circunferências Secantes – são aquelas
circunferências que possuem apenas dois pontos
em comum.

16.  Circunferências Tangentes Interiores –
quando têm apenas um ponto em comum e a
distância entre seus centros é menor que a
diferença entre seus raios.

17.  Circunferências Internas – não tem nenhum
ponto em comum, e uma delas é interna à outra.

18.  Circunferências Concêntricas – quando duas
ou mais circunferências possuem o mesmo centro,
mas os raios são diferentes.

19.  A região do plano limitada por duas
circunferências concêntricas é chamada de
COROA CIRCULAR.