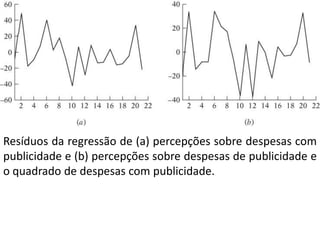
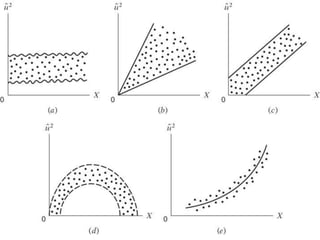
06 tópico 5 - heterocedasticidade

Econometria
Tópico 4 – Regressão Múltipla
Quebra dos pressupostos: Heterocedasticidade
Ricardo Bruno N. dos Santos
Professor Adjunto da Faculdade de Economia
e do PPGE (Economia) UFPA

Lembre-se que os vídeos necessários para o
acompanhamento dessa apresentação são todos os
vídeos que iniciam por 07, e encontram-se dentro da
pasta Vídeos no mediafire.
Link do mediafire:
http://www.mediafire.com/?q1dbpxh1b4uxo
No Slideshare:

Quebra dos pressupostos:
Heterocedasticidade
Natureza da Heterocedasticidade
A heterocedasticidade quebra uma das mais relevantes e
importantes hipóteses do MRLC, trata-se da
homocedasticidade dos resíduos onde:
𝐸 𝑢𝑖
2
= 𝜎2
𝑖 = 1,2, … , 𝑛
A variância condicional de 𝑌𝑖 aumenta a medida que uma
determinada variável independente aumenta. Ou seja, a
variância de 𝑌𝑖 não são as mesmas. Como a variância do
resíduo está condicionada a 𝑌𝑖 então existe a presença da
heterocedasticidade, onde
𝐸 𝑢𝑖
2
= 𝜎𝑖
2
Suponha que o seguinte modelo esteja sendo analisado, onde
𝑌𝑖 = 𝛽1 + 𝛽2 𝑋𝑖 + 𝑢𝑖, e Y seja a poupança e X a renda, assim
podemos verificar os dois seguintes gráficos:

HOMOCEDASTICIDADE

HETEROCEDASTICIDADE

Heterocedasticidade
As seguintes razões podem constituir-se como elementos de
variabilidade de 𝑢𝑖, como:
1) Seguindo os modelos de erro-aprendizagem,
comportamentos incorretos das pessoas diminuem com o
tempo ou o número de erros torna-se mais consistente. Neste
caso, espera-se que 𝜎𝑖
2
diminua. Como exemplo o autor cita a
Figura 11.3, que relaciona o número de erros de digitação
cometidos em um dado período de tempo em um teste com
as horas de prática de digitação. Percebe-se que o erro de
digitação diminui a medida que temos mais prática.

Heterocedasticidade
2) A medida que a renda aumenta, as pessoas têm mais renda
discricionária e, portanto, mais opções para escolher como
aplicarão sua renda. Por isso, é provável que 𝜎𝑖
2
aumente com
a renda. Assim, na regressão de poupanças contra a renda é
provável que se verifique que 𝜎𝑖
2
aumenta com a renda, pois
as pessoas têm maior opção sobre como irão dispor de suas
poupanças. Do mesmo modo, em geral se espera que a
empresas com lucros maiores mostrem maior variabilidade
em suas políticas de dividendos que aquelas com lucros mais
baixos.

Heterocedasticidade
3) A medida que as técnicas de coleta de dados aprimoram-
se, é provável que 𝜎𝑖
2
diminua. Assim, os bancos que têm
equipamentos sofisticados de processamento de dados
provavelmente cometem menos erros nos demonstrativos
periódicos de seus clientes do que bancos sem esses
recursos.
4) A hetero também ocorre com a presença de dados
discrepantes (outliers)

Heterocedasticidade
5) Violação da hipótese 9, onde o modelo de regressão deve ser
especificado corretamente.
6) A assimetria é outra fonte de heterocedasticidade. Renda e
riqueza são variáveis que geralmente são desiguais, onde a maior
parte da renda encontra-se na menor parte da população. Isso
gera uma assimetria no dado.
7) Transformação incorreta de dados. É mais comum em dados de
corte transversal do que nas séries temporais. A diferença é que
no primeiro temos um nível de desagregação maior da
informação, ou seja, estamos avaliando-a em vários níveis (como
os diferentes níveis de renda municipal). Já a série temporal é um
dado mais agregado, que não sofre grandes variações.

Resíduos da regressão de (a) percepções sobre despesas com
publicidade e (b) percepções sobre despesas de publicidade e
o quadrado de despesas com publicidade.

Heterocedasticidade
Estimativa dos MQO na presença da Heterocedasticidade
A pergunta que se faz é: o que acontece com o MQO e suas
variâncias se introduzirmos a heterocedasticidade fazendo
𝐸 𝑢𝑖
2
= 𝜎𝑖
2
, mas mantivermos todas as demais hipóteses do
modelo clássico? Vamos analisar o modelo com duas
variáveis:
𝑌𝑖 = 𝛽1 + 𝛽2 𝑋𝑖 + 𝑢𝑖
Verificamos que:
𝛽2 =
𝑥𝑖 𝑦𝑖
𝑥𝑖
2
=
𝑛 𝑋𝑖 𝑌𝑖 − 𝑋𝑖 𝑌𝑖
𝑛 𝑋𝑖
2
− 𝑋𝑖
2

Heterocedasticidade
Bem como a variância do beta 2 estimado é dada por:
𝑣𝑎𝑟 𝛽2 =
𝑥𝑖
2
𝜎𝑖
2
𝑥𝑖
2 2
𝑣𝑎𝑟( 𝛽2) =
𝜎2
𝑥𝑖
2
O que mantém o modelo aderente ao MELNT é a variância
constante 𝜎2, mas, o que acontece que ela não for constante?
Para verificar isso temos que analisar os resultados para dois
aspectos um considerando a tendenciosidade e outro
considerando a eficiência do modelo.

Heterocedasticidade
O fato de ser homocedástica ou heterocedástica não
influencia na tendenciosidade do estimador 𝛽2 (ver apêndice
3A do capítulo 3), onde 𝐸 𝛽2 = 𝛽2 , onde mesmo na
presença de heterocedasticidade, em amostras grandes o
estimador continua consistente, e portanto, não tendencioso.
Porém a eficiência é algo que não pode ser mantido. Pois
dada a presença de heterocedasticidade ele deixa de
apresentar a variância mínima, ou seja, ele deixa de ser
MELNT. Isso porque:
𝑣𝑎𝑟 𝛽2 =
𝑥𝑖
2
𝜎𝑖
2
𝑥𝑖
2 2
Aumenta conforme 𝜎𝑖
2

Heterocedasticidade
O Método do Mínimos Quadrados Generalizados (MQG)
Pelo fato de o estimador deixar de ser MELNT temos que
encontrar uma forma de tornar o estimador MELNT, para
tanto, é utilizado o MQG. Basicamente tal método incorpora
pesos ou importâncias que ajudam a explicar o
comportamento da variância, ou seja, considerar o seu efeito
na hora do cálculo do estimador.
Considerando a fórmula para o modelo simples:
Para facilitar o entendimento da operação algébrica vamos
inserir a variável X0 que representa uma matriz vetor de 1,
assim
𝑌𝑖 = 𝛽1 𝑋0𝑖 + 𝛽2 𝑋𝑖 + 𝑢𝑖 𝑋0𝑖 = 1 𝑝𝑎𝑟𝑎 𝑐𝑎𝑑𝑎 𝑖

Heterocedasticidade
Se conhecermos as variâncias 𝜎𝑖
2
poderemos inseri-las
na equação como um peso, ou seja:
𝑌𝑖
𝜎𝑖
2
= 𝛽1
𝑋0𝑖
𝜎𝑖
2
+ 𝛽2
𝑋𝑖
𝜎𝑖
2
+
𝑢𝑖
𝜎𝑖
2
𝑌𝑖
𝜎𝑖
= 𝛽1
𝑋0𝑖
𝜎𝑖
+ 𝛽2
𝑋𝑖
𝜎𝑖
+
𝑢𝑖
𝜎𝑖
𝑌𝑖
∗
= 𝛽1
∗
𝑋0𝑖
∗
+ 𝛽2
∗
𝑋𝑖
∗
+ 𝑢𝑖
∗
Onde o sobrescrito com asteriscos nos parâmetros indicam os
estimadores do modelo transformado, para podermos
distingui-los dos parâmetros do modelo do MQO.

Heterocedasticidade
O que vai chamar a atenção é o erro transformado, vamos
verificar como ficam sua variância após a transformação:
𝑣𝑎𝑟 𝑢𝑖
∗
= 𝐸 𝑢𝑖
∗
= 𝐸
𝑢𝑖
𝜎𝑖
2
𝑝𝑜𝑟 𝐸 𝑢𝑖
∗
= 0
=
1
𝜎𝑖
2 𝐸 𝑢𝑖
2
𝑗á 𝑞𝑢𝑒 𝜎𝑖
2
é 𝑐𝑜𝑛ℎ𝑒𝑐𝑖𝑑𝑜
=
1
𝜎𝑖
2 𝜎𝑖
2
𝑗á 𝑞𝑢𝑒 𝐸 𝑢𝑖
2
= 𝜎𝑖
2
= 1
Ou seja, passamos a provar que a variância do modelo do
MQG é uma constante, ou seja, torna-se homocedástico.
Conservando as hipóteses do modelo clássico de regressão
linear, assim, se aplicarmos o MQO no modelo transformado,
ele irá gerar os MELNT.

Heterocedasticidade
Assim 𝛽1
∗
e 𝛽2
∗
são MELNT e não se tratam dos estimadores de
MQO 𝛽1 e 𝛽2.
Podemos verificar, portanto, que o MQG são os MQO nas
variáveis transformadas que satisfazem as hipóteses padrão
de Mínimos Quadrados.
Podemos, assim como realizado o procedimento para MQO,
encontrar o resíduo mínimo para a função transformada,
considerando, portanto:
𝑌𝑖
∗
= 𝛽1
∗
𝑋0𝑖
∗
+ 𝛽2
∗
𝑋𝑖
∗
+ 𝑢𝑖
∗
Para obter o MQG temos que minimizar os resíduos, logo

Heterocedasticidade
𝑢𝑖
2∗
= 𝑌𝑖
∗
− 𝛽1
∗
𝑋0𝑖
∗
− 𝛽2
∗
𝑋𝑖
∗ 2
𝑢𝑖
𝜎𝑖
2
=
𝑌𝑖
𝜎𝑖
− 𝛽1
∗
𝑋0𝑖
𝜎𝑖
− 𝛽2
∗
𝑋𝑖
𝜎𝑖
2
Para o 𝛽2
∗
o estimador de MQG será:
𝛽2
∗
=
𝑤𝑖 𝑤𝑖 𝑋𝑖 𝑌𝑖 − 𝑤𝑖 𝑋𝑖 𝑤𝑖 𝑌𝑖
𝑤𝑖 𝑤𝑖 𝑋𝑖
2
− 𝑤𝑖 𝑋𝑖
2
E a variância será:
𝑣𝑎𝑟 𝛽2
∗
=
𝑤𝑖
𝑤𝑖 𝑤𝑖 𝑋𝑖
2
2
Onde 𝑤𝑖 =
1
𝜎𝑖
2

Heterocedasticidade
Podemos então verificar que a diferença entre o MQO e o
MQG é dada pela presença de um termo ponderado
visualizado pela soma ponderada dos quadrados dos resíduos
𝑤𝑖 = 1/𝜎𝑖
2
, que tem um papel de peso, no entanto, os
resultados de ambos (MQO e MQG) chegam a mesma
conclusão de que os resíduos são homocedásticos.
A diferença entre o uso das duas situações pode ser
observado no próximo diagrama de dispersão. Nos MQO,
cada 𝑢𝑖
2
associado aos pontos A, B e C receberá o mesmo
peso quando da SQR for minimizada. É claro que, nesse caso,
a 𝑢𝑖
2
associada ao ponto C dominará a SQR. Já nos MQG, a
observação extrema C receberá um peso relativamente
menor que as outras duas observações.

Heterocedasticidade
Consequências de usar MQO na presença de
heterocedasticidade
A regra aqui é verificar e responder o que acontece quando os
nossos estimadores não são eficientes.
Vamos para essa dinâmica, continuar utilizando o 𝛽2 e a sua
respectiva fórmula da variância (sabendo da existência da
hetero), que considera a presença da heterocedasticidade. O
grande problema é que mesmo conhecendo a variância 𝜎𝑖
2
não podemos estabelecer um intervalo de confiança e muito
menos realizar os testes t e F, pois os intervalos de confiança
baseados na estimativa do 𝛽2 são menores, isso porque é
possível mostrar que var( 𝛽2
∗
) ≤ 𝑣𝑎𝑟( 𝛽2 ).

Heterocedasticidade
O grande problema é considerar a estimação por MQO e
desconsiderar a heterocedasticidade. Em primeiro lugar,
𝑣𝑎𝑟( 𝛽2 ) = σ2/ 𝑥𝑖
2
é um estimador TENDENCIOSO da
𝑣𝑎𝑟 𝛽2 = 𝑥𝑖
2
𝜎𝑖
2
/ 𝑥𝑖
2 2
, isso porque na média ele
sobrestima ou subestima a variância, e, em geral, não
podemos dizer se o viés é positivo (sobreestimação) ou
negativo (subestimação), pelo fato de isso depender da
natureza da relação entre 𝜎𝑖
2
e os valores assumidos pela
variável explanatória X, como observado pelo termo 𝑥𝑖
2
do
denominador da fórmula da variância.
O viés surge do fato de o valor de 𝜎2
dado por 𝑢𝑖
2
/(𝑛 − 2),
não ser mais um estimador NÃO TENDENCIOSO deste último
quando a heterocedasticidade está presente.

Heterocedasticidade
Caso persistamos no uso dos procedimentos comuns de teste
apesar da hetero, quaisquer que sejam as conclusões a que
chegamos ou as inferências que fizermos poderão ser
equivocadas.
Para termos um entendimento melhor do que ocorre, vamos
verificar um estudo de Monte Carlo conduzido por Davidson e
MacKinnon, eles consideram o seguinte modelo simples, que em
nossa notação é:
Os autores pressupõem que 𝛽1 = 1 e 𝛽2 = 1 e 𝑢𝑖~𝑁(0, 𝑋𝑖
𝛼
).
Como mostra a última expressão, os autores supõem que a
variância de erro seja heterocedástica e relacionada ao valor do
regressor X com poder . Se por exemplo, =1, a variância do erro
é proporcional ao valor de X, caso seja =2, a variância do resíduo
será proporcional ao quadrado do valor de X e assim por diante.

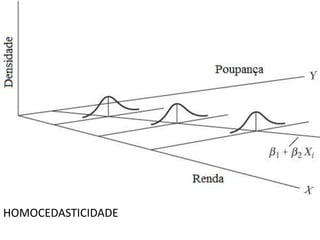
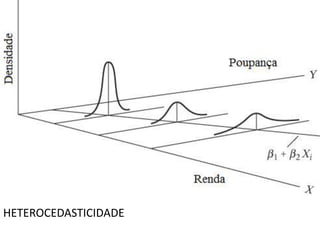
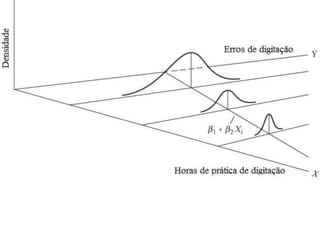
Heterocedasticidade
Baseado em 20 mil réplicas e permitindo vários valores para
, eles obtêm erros padrão dos dois coeficientes de regressão
usando os MQO (com 𝑣𝑎𝑟( 𝛽2 ) = σ2/ 𝑥𝑖
2
), MQO
permitindo a heterocedásticidade (onde 𝑣𝑎𝑟 𝛽2 =
𝑥𝑖
2
𝜎𝑖
2
/ 𝑥𝑖
2 2
), e o MQG ( com 𝑣𝑎𝑟 𝛽2
∗
= 𝑤𝑖 /
[ 𝑤𝑖 𝑤𝑖 𝑋𝑖
2
2])
Os resultados foram obtidos por cada peso de .

Heterocedasticidade
Os autores observaram que sempre o MQO sobrestima o
MQG (ou seja, sempre suas variâncias serão maiores que o
MQO), tanto para o intercepto quanto para o coeficiente
angular.
Com isso a conclusão é que e na presença da
heterocedasticidade são os MQG e não os MQO os MELNT.

Heterocedasticidade
Detecção da Heterocedasticidade
Vamos observa alguns procedimentos práticos que ajudam na
detecção da heterocedasticidade. Para dados
socioeconômicos é mais difícil a detecção pois não temos
controle da amostra, dessa forma temos muitas vezes que
fazer uso da intuição, informações preexistentes, experiência
empírica e muitas vezes mera especulação.
Tendo em vista esses pontos, vamos observar alguns métodos
informais e formais para a detecção da hetero.

Heterocedasticidade
Os métodos informais: consistem basicamente verificar o
comportamento dos resíduos ao quadrado 𝑢𝑖
2
contra o valor
estimado de Y 𝑌𝑖. Algum comportamento sistemático entre
essas duas relações pode nos ajudar a concluir pela existência
da heterocedasticidade na regressão.
A seguir podemos observar algumas situações gráficas que
indicam a existência ou não de um comportamento
sistemático entre essas duas variáveis.

Heterocedasticidade
Esse comportamento pode ser observado também entre os
resíduos e as variáveis independentes X. Caso o resíduo ao
quadrado tiver alguma relação sistemática com alguma
variável independente, é um indicativo forte da presença de
heterocedasticidade na regressão.

Heterocedasticidade
Métodos formais: Tratam-se dos testes para verificação da
existência ou não da heterocedasticidade. São testes que são
realizados com base nos resíduos da regressão. A grande
maioria parte do pressuposto que na regressão existe
homocedasticidade, portanto, a hipótese nula do teste
consiste em:
𝐻0: 𝐻𝑜𝑚𝑜𝑐𝑒𝑑𝑎𝑠𝑡𝑖𝑐𝑖𝑑𝑎𝑑𝑒
𝐻1: 𝐻𝑒𝑡𝑒𝑟𝑜𝑐𝑒𝑑𝑎𝑠𝑡𝑖𝑐𝑖𝑑𝑎𝑑𝑒
Aqui será abordado apenas 3 testes, a ideia é entender a
dinâmica de cada um deles.

Heterocedasticidade
Teste de Glejser: Trata-se de um método que procura verificar
a relação entre resíduos e o comportamento da variável
independente X. O teste consiste em duas etapas, onde:
1ª Estimar a regressão: Devemos primeiramente estimar a
nossa regressão de interesse em que supõe-se ter a presenta
da hetero:
2ª Etapa: Depois de estimada a regressão, pegamos o resíduo
estimado na sua forma absoluta | 𝑢𝑖| e usamos ele como
variável dependente do modelo contra a variável
independente do modelo anterior, no entanto, essa variável
pode ser transformada conforme o comportamento dos
resíduos, os modelos podem ser os seguintes:

Heterocedasticidade
𝑢𝑖 = 𝛽1 + 𝛽2 𝑋𝑖 + 𝑣𝑖
𝑢𝑖 = 𝛽1 + 𝛽2
1
𝑋 𝑖
+ 𝑣𝑖
𝑢𝑖 = 𝛽1 + 𝛽2
1
𝑋 𝑖
+ 𝑣𝑖
𝑢𝑖 = 𝛽1 + 𝛽2 𝑋𝑖
2
+ 𝑣𝑖
O grande problema nesse teste são os resíduos 𝑣𝑖 que podem
ter comportamento heterocedástico também.

Heterocedasticidade
As regressões com o comportamento 𝑢𝑖 = 𝛽1 + 𝛽2 𝑋𝑖 + 𝑣𝑖
são mais difíceis de serem estimadas por serem modelos de
regressão não linear. O que inviabiliza sua estimação por
MQO.
O exemplo a seguir irá fazer uso das informações sobre
remuneração e produtividade e será utilizados os dados da
tabela 11.1.

Heterocedasticidade
Teste de Breusch-Pagan-Godfrey (BPG): É um dos testes de
heterocedasticidade mais conhecidos e utilizados. Para
entende-lo é necessária a construção de cinco etapas que
culminará numa análise da estatística 2.
Para iniciar o teste vamos recorrer ao modelo de regressão
com k variáveis.
𝑌𝑖 = 𝛽1 + 𝛽2 𝑋2𝑖 + ⋯ + 𝛽 𝑘 𝑋 𝑘𝑖 + 𝑢𝑖
Suponha que variância do erro, 𝜎𝑖
2
, seja descrita como:
𝜎𝑖
2
= 𝑓(𝛼1 + 𝛼2 𝑍2𝑖 + ⋯ + 𝛼 𝑚 𝑍 𝑚𝑖)
Ou seja, 𝜎𝑖
2
é uma função das variáveis não estocásticas Z;
alguns ou todos os X podem servir de Z. Suponha que
𝜎𝑖
2
= 𝛼1 + 𝛼2 𝑍2𝑖 + ⋯ + 𝛼 𝑚 𝑍 𝑚𝑖

Heterocedasticidade
Onde 𝜎𝑖
2
passa a ser uma função linear de Z. Caso 𝛼2 = 𝛼3 =
⋯ = 𝛼 𝑚 = 0, e 𝜎𝑖
2
= 𝛼1, que é uma constante. Dessa forma,
para testar se 𝜎𝑖
2
é homocedástico, podemos testar a
hipótese de que 𝛼2 = 𝛼3 = ⋯ = 𝛼 𝑚 = 0, esta é a ideia
básica por trás do teste de BPG.
Os procedimentos para a realização do teste são os seguintes:
1ª Etapa: Estime 𝑌𝑖 = 𝛽1 + 𝛽2 𝑋2𝑖 + ⋯ + 𝛽 𝑘 𝑋 𝑘𝑖 + 𝑢𝑖 por MQO
e obtenha os resíduos 𝑢𝑖.
2ª Etapa: Devemos obter o 𝜎2 = 𝑢𝑖
2
/𝑛. Que é o estimador
de máxima verossimilhança de 𝜎2
. Essa fórmula é diferente
do estimador de MQO que é 𝜎2
= 𝑢𝑖
2
/(𝑛 − 𝑘).
3ª Etapa: Construir as variáveis 𝑝𝑖 que são definidas como:
𝑝𝑖 = 𝑢𝑖
2
/ 𝜎2

Heterocedasticidade
4ª Etapa: Faça a regressão 𝑝𝑖 construída sobre os Z como
𝑝𝑖 = 𝛼1 + 𝛼2 𝑍2𝑖 + ⋯ + 𝛼 𝑚 𝑍 𝑚𝑖 + 𝑣𝑖
5ª Etapa: Obtenha a SQE (Soma dos Quadrados Explicada) e
defina:
 =
1
2
𝑆𝑄𝐸
Pressupondo que os resíduos se distribuem normalmente,
podemos demostrar que, se há homocedasticidade e se o
tamanho da amostra n aumenta indefinidamente, então:
 𝑎𝑠𝑦~ 𝑚−1
2

Heterocedasticidade
Para prática do teste BPG vamos utilizar os dados da Tabela
11.3.
Teste GERAL de Heterocedasticidade de White: É o mais
dinamizado dos testes, diante dos demais testes já vistos é o
que possui menos problemas, isso porque ele não necessita
que o pressuposto de normalidade seja atendido (conforme
ocorre com o teste BPG) e não possui nenhuma restrição
quanto aos resíduos de sua regressão auxiliar tiver algum
problema de heterocedasticidade.
Tanto, que é baseado no teste de White que são feitas a
maior parte das correções da hetero em modelos de
regressão linear.

HeterocedasticidadeO teste para ser visualizado necessita passar por quatro etapas,
sempre partindo do modelo de regressão onde:
𝑌𝑖 = 𝛽1 + 𝛽2 𝑋2𝑖 + 𝛽3 𝑋3𝑖 + 𝑢𝑖
1ª Etapa: Estimar a regressão acima e encontrar os resíduos
estimados 𝑢𝑖.
2ª Etapa: De porte dos resíduos calculamos a seguinte regressão
auxiliar:
𝑢𝑖
2
= 𝛼1 + 𝛼2 𝑋2𝑖 + 𝛼3 𝑋3𝑖 + 𝛼4 𝑋2𝑖
2
+ 𝛼5 𝑋3𝑖
2
+ 𝛼6 𝑋2𝑖 𝑋3𝑖 + 𝑣𝑖
Em seguida será obtido o R2 da regressão auxiliar.
3ª Etapa: Sob a hipótese nula de que não há heterocedasticidade,
pode-se mostrar que o tamanho da amostra (n) multiplicado pelo
R2 da regressão auxiliar segue uma distribuição qui-quadrado com
graus de liberdade iguais ao número de regressores (excluindo-se
o intercepto – constante) na regressão auxiliar. Ou seja,

Heterocedasticidade
𝑛𝑅 𝑎𝑠𝑠
2 ~ 𝑔𝑙
2
Com caso do modelo com três variáveis irá gerar na regressão
auxiliar outras três variáveis, com isso teremos 5 graus de
liberdade uma vez que (n-1) = (6-1)
4ª Etapa: Comparamos o valor do Qui-quadrado calculado
com o valor tabelado, caso o calculado seja maior que o
tabelado, teremos então a rejeição da hipótese nula, ou seja,
rejeição da homocedasticidade, logo a conclui-se pela
presença da heterocedasticidade.
Caso ele não seja significativo, estaremos concluindo que
𝛼2 = 𝛼3 = 𝛼4 = 𝛼5 = 𝛼6 = 0
Ou seja, de que os resíduos são homocedásticos.

Heterocedasticidade
Para ilustrar o exemplo do teste de White, será feito o
exemplo conforme o exercício 11.15 (pág. 349). Fazendo uso
da Tabela 11.7. Também iremos executar os testes de
heterocedasticidade de White e o BPG pelo Gretl.
Qual o melhor teste? Não se trata de uma decisão fácil, uma
vez que tais testes baseiam-se em vários pressupostos. Ao
compararmos os testes, precisamos prestar atenção ao seu
tamanho (ou nível de significância), potência (a probabilidade
de rejeitarmos a hipótese falsa) e a sensibilidade a
discrepância (Outliers). O teste de White por exemplo é um
teste que tem baixa potência contra outros testes. Já o BPG é
sensível a presença da normalidade dos resíduos.

Heterocedasticidade
Medidas corretivas
Verificamos que a presença da hetero irá afetar a eficiência de
nossos estimadores. Podemos aplicar medidas corretivas
levando em conta dois aspectos, quando conhecemos a
variância (𝜎𝑖
2
) e quando não a conhecemos.
𝝈𝒊
𝟐
Conhecido: uso dos Mínimos Quadrados Ponderados.
Quando aplicamos o MQP corrigimos a heterocedasticidade,
tornando os estimadores MELNT. A melhor forma de verificar
o procedimento (que já foi utilizado em outra oportunidade)
e verificá-lo na prática. Para tanto, será usado o exemplo da
Tabela 11.1 conforme exemplo 11.7 da página 336.

Heterocedasticidade
𝝈𝒊
𝟐
Desonhecido
Quando o valor da variância do erro é desconhecida é
possível fazer uma correção através de mudanças das
matrizes de variância e covariância (var-cov). O processo mais
conhecido é a correção de White.
Mas antes é interessante falar em como se da essa correção,
e mostrar no Gretl como essa correção procede.
A correção de White na verdade ocorre com a inserção da
matriz de pesos de White no cálculo da variância do
estimador, onde:
𝑣𝑎𝑟 𝛽𝑗 =
𝑤𝑗𝑖 𝑢𝑖
2
𝑤𝑗𝑖
2 2

Heterocedasticidade
O termo 𝑤𝑗 são os resíduos da regressão auxiliar de White,
como antes verificado para o modelo de três variáveis:
𝑢𝑖
2
= 𝛼1 + 𝛼2 𝑋2𝑖 + 𝛼3 𝑋3𝑖 + 𝛼4 𝑋2𝑖
2
+ 𝛼5 𝑋3𝑖
2
+ 𝛼6 𝑋2𝑖 𝑋3𝑖 + 𝑣𝑖
A forma matricial de se mostrar esse regressor é:
𝑣𝑎𝑟 𝛽𝑗 = 𝑋′ 𝑋 −1 𝑋′𝑋 𝑋′ 𝑋 −1 = 𝐻𝐶0
Essa primeira matriz é o termo do Gretl usado para a correção
de White.
Para o HC1 teremos uma correção na matriz de White pelo
grau de liberdade onde:
𝑢𝑖
2
×
𝑛
𝑛 − 𝑘

Heterocedasticidade
Para o termo HC2 teremos será feita uma correção ortogonal
cuja expectativa dos resíduos será dada por:
𝑢𝑖
2
1 − ℎ𝑖
onde ℎ𝑖 = 𝑋𝑖 𝑋′ 𝑋 −1 𝑋𝑖
O HC3 é uma versão com a correção Jackknife, onde na
verdade há uma sobrecorreção dada por:
𝑢𝑖
2
1 − ℎ𝑖
2

Heterocedasticidade
Vamos verificar o processo de correção de White no Gretl
utilizando o exemplo da Tabela 11.5 sobre dados de inovações
na América Latina, que encontra-se dentro do exemplo 11.10
da página 342.

Heterocedasticidade
Uma Advertência: Segundo John Fox
“Só vale a pena corrigir variâncias desiguais do erro somente
quando o problema for grave. O impacto da variância do erro
não constante sobre a eficiência do estimador de MQO e na
validade da eficiência dos MQO depende de vários fatores,
inclusive do tamanho da amostra, do grau de variação no 𝜎𝑖
2
,
da configuração dos valores de X [regressor – ou variáveis
independentes] e da relação entre a variância dos erros e os
X. Portanto, não é possível chegar a conclusões gerais a
respeito dos danos produzidos pela heterocedásticidade.”

06 tópico 5 - heterocedasticidade

Mais conteúdo relacionado

Mais procurados

Semelhante a 06 tópico 5 - heterocedasticidade

Mais de Ricardo Bruno - Universidade Federal do Pará

Último

06 tópico 5 - heterocedasticidade