Este documento apresenta uma apostila sobre introdução ao estudo de funções elaborada pelo professor Carlinhos. A apostila define o conceito de função de forma intuitiva e matemática, apresenta exemplos de funções, explica como identificar o domínio, imagem e contradomínio de uma função, e como construir e analisar gráficos de funções. A apostila também contém exercícios de fixação sobre o assunto.

1. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
1
ESCOLA DR. ALFREDO JOSÉ BALBI
UNITAU
APOSTILA
INTRODUÇÃO AO ESTUDO DAS FUNÇÕES
PROF. CARLINHOS
NOME: NO
:

2. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
2
FUNÇÃO
IDÉIA INTUITIVA DE FUNÇÃO
O conceito de função é um dos mais importantes da matemática. Ele está sempre
presente na relação entre duas grandezas variáveis. Assim são exemplos de funções:
- O valor a ser pago numa corrida de táxi é função do espaço percorrido;
- A área de um quadrado é função da medida do seu lado;
- O consumo de combustível de um automóvel é função, entre outros fatores, da
velocidade.
Observe que as relações que vimos a seguir têm duas características em comum:
- A todos os valores da variável independente estão associados valores da variável
dependente;
- Para um dado valor da variável independente está associado um único valor da
variável dependente.
As relações que têm essas características são chamadas de funções.
Exemplos:
1) Nos itens abaixo, estão descritas algumas relações entre variáveis. Em cada caso,
identifique a variável independente e a dependente.
a) O número de refrigerante que uma pessoa compra e a quantia a ser paga.
Resolução:
b) A duração de uma chamada telefônica e o custo da chamada.
Resolução:
2) O preço a ser pago por uma corrida de táxi inclui uma parcela fixa de R$ 6,00 ,
denominada bandeirada mais uma parcela variável de R$ 0,90 por km rodado.
Determine:
a) A função que representa o preço P de uma corrida em função de x quilômetros
rodados.
Resolução:
b) O preço de uma corrida de 12 km.
Resolução:
c) A distancia percorrida por um passageiro que pagou R$ 96,00 pela corrida.
Resolução:

3. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
3
DEFINIÇÃO MATEMÁTICA DE FUNÇÃO
Sendo A e B dois conjuntos não vazios e uma relação f de A em B, essa relação f é uma
função quando cada elemento x do conjunto A está associado a um, e somente um,
elemento y do conjunto B. Indica-se por:
Quando estas condições descritas na definição não forem satisfeitas, existirá apenas uma
relação (R). Daí, concluímos que toda função é uma relação mas, nem toda relação e
uma função.
Observe os exemplos com diagramas:
As figuras 1, 2 e 3 representam funções. Note que cada elemento do conjunto domínio
A tem uma única chegada no conjunto contradomínio B. Chamamos de conjunto
imagem (Im) aos elementos de B que se relacionaram com os elementos de A. No
conjunto contradomínio pode sobrar elemento. A letra f acima do diagrama indica que a
relação especial é uma função.
fig.1 fig.2 fig.3
As figuras 4, 5 e 6 representam apenas relações. Note que na fig. 4 alguns elementos de
A têm duas chegadas em B, na fig. 5 sobrou um elemento de A sem relacionar-se com B
e, finalmente, na fig. 6 um único elemento de A têm várias chegadas em B. A letra R
acima do diagrama indica ser apenas uma relação.
fig.4 fig.5 fig.6
Exemplos
1) Dados A = { -3, -2, 0, 3 } e B = { - 1, 0, 1, 2, 4, 5, 7 } e uma relação expressa pela
fórmula y = x + 2, com x pertencendo a A e y pertencendo a B.
a) Faça o diagrama e verifique se f é uma função de A em B.
Resolução:
b) Se for uma função de A em B, determine o domínio, a imagem e o contra-domínio de
f.
Resolução:
2) Seja a função f: definida por f(x) = x2
- 7x + 9. Determine:
f: A B

4. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
4
a) O valor de f(-1)
Resolução:
b) Os valores de x para que se tenha f(x) = -1.
Resolução:
3) Dadas as funções f(x) = 4x + 3 e g(x) = x2
+ a. Sabendo que f(2) - g(1) = 3, calcule o
valor de a.
Resolução:
4) Dada a função f: definida por f(x) = ax + b, com a e b ℜ∈ . Determine a e b,
sabendo que f(1) = 3 e f(2) = 5.
Resolução:
DOMINIO DE UMA FUNÇÃO REAL DE VARIÁVEL REAL
Quando trabalhamos com uma função, é importante sabermos qual o domínio dessa
função, pois é ele que vai determinar os valores possíveis para a variável independente.
Em muitos casos, o domínio e o contradomínio não vêm explicitados, devemos, então,
considerar como domínio o conjunto de todos os números reais que podem ser
colocados no lugar da variável independente na fórmula da função, obtendo, após os
cálculos, um número real, já, o contradomínio será os números reais.
Exemplos
1) Encontrar o domínio das funções:
a) f(x) = 3x2
- 4x + 2 b) f(x) =
42
53
−
−
x
x
Resolução: Resolução:
c) f(x) = 44 −x d) f(x) =
4
33
2
5
−
−
+
+
−
x
x
x
x
Resolução: Resolução:

5. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
5
GRÁFICO DE UMA FUNÇÃO
Para construir o gráfico de uma função, utilizaremos o sistema de coordenadas
cartesianas ortogonais.
O sistema de coordenadas ortogonais é composto por:
- Duas reta perpendiculares entre si, onde a reta horizontal é o eixo x (abscissas) e a reta
vertical o eixo y (ordenadas).
- O cruzamento das duas retas é a origem do sistema.
- As retas dividem o plano em quatro partes iguais chamadas de quadrantes.
O gráfico é conjunto de todos os pontos (x;y) do plano cartesiano, com x∈D e y∈Im.
Para isso, consideremos os valores do domínio da função o eixo x e as respectivas
imagens no eixo y.
Exemplos:
1) Construir o gráfico das funções:
a) BA:f → , definida por f(x) = x + 2, sendo A = { -1; 0; 1; 2 } e B = { 1; 2; 3; 4; 5 }
b) f: definida por f(x) = x + 2

6. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
6
ANALISANDO GRÁFICOS DE FUNÇÕES
A partir do gráfico de uma função, podemos obter informações importantes sobre o
comportamento dessa função, como:
- O domínio e a imagem.
- Os pontos onde o gráfico intercepta os eixos coordenados.
- Os intervalos para os quais a função é crescente, decrescente ou constante.
- Os intervalos para os quais a o valor da função é positivo e negativo.
- O valor máximo ou mínimo que a função atinge.
- O (s) valor (es) da(s) raiz(es) da função.
Como reconhecer quando um gráfico representa uma função
Como para cada valor de x do domínio devemos ter em correspondência um único y do
contradomínio, é possível identificar se um gráfico representa ou não função, traçamos
retas paralelas ao eixo y. Para ser função, cada reta vertical traçada por pontos do
domínio deve interceptar o gráfico em um único ponto.
Como determinar o domínio e a imagem da função
- O domínio de uma função é obtido pela projeção dos pontos do gráfico sobre o eixo
x (abscissas)
- A imagem de uma função é obtida pela projeção dos pontos do gráfico sobre o eixo
y (ordenadas)
Exemplo
D(f) = }6x/1x{ ≤≤ℜ∈
Im(f) = }5y2/y{ ≤≤ℜ∈

7. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
7
Como determinar as raízes ou os zeros de uma função
Graficamente a(s) raiz(es) de uma função é(são) a(s) a(s) abscissa(s) do(s) ponto(s) onde
o gráfico encontra o eixo x (abscissas).
Exemplo
Como determinar o intervalo onde a função é crescente, decrescente ou constante
- Se aumentarmos o valor da variável independente e aumentar os valores da imagem,
temos função crescente.
- Se aumentarmos o valor da variável independente e diminuir os valores da imagem,
temos função decrescente.
Se aumentarmos o valor da variável independente e não alterar os valores da imagem,
temos função constante.
Valor máximo e Valor mínimo de uma função
Logo, os números 2 e 5 são as raízes ou os
zeros da função
constante
decrescente
crescente
y
o
x
y
o
x
X1 X2
f(x1)
f(x2)
máximo
mínimo
Valor máximo f(x2)
Valor mínimo f(x1)

8. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
8
EXERCÍCIOS DE FIXAÇÃO DA APRENDIZAGEM
1) (Unesp) Uma pessoa obesa, pesando num certo momento 156 kg, recolhe-se a um SPA onde se
anunciam perdas de peso de até 2,5 kg por semana. Suponhamos que isso realmente ocorra. Nessas
condições:
a) Encontre uma fórmula que expresse o peso mínimo, P, que essa pessoa poderá atingir após n semanas.
resp: 156 – 2,5n
b) Calcule o número mínimo de semanas completas que a pessoa deverá permanecer no SPA para sair de
lá com menos de 120 kg de peso. resp: 15 semanas
2) (Unicamp) Para transformar graus Fahrenheit em graus centígrados usa-se a fórmula:
C = 5(F - 32)/9,onde F é o número de graus Fahrenheit e C é o número de graus centígrados.
a) Transforme 35 graus centígrados em graus Fahrenheit. resp: 95
b) Qual a temperatura (em graus centígrados) em que o número de graus Fahrenheit é o dobro do número
de graus centígrados? resp: 160
3) (Fuvest) A função que representa o valor a ser pago após um desconto de 3% sobre o valor x de uma
mercadoria é: resp: b
a) f(x) = x – 3 b) f(x) = 0,97x c) f(x) = 1,3x d) f(x) = -3x e) f(x) = 1,03x
4) (Puccamp) Para produzir um número n de peças (n inteiro positivo), uma empresa deve investir
R$200000,00 em máquinas e, além disso, gastar R$0,50 na produção de cada peça. Nessas condições, o
custo C, em reais, da produção de n peças é uma função de n dada por:
a) C(n) = 200 000 + 0,50 resp: c
b) C(n) = 200 000n
c) C(n) = n/2 + 200 000
d) C(n) = 200 000 - 0,50n
e) C(n) = (200 000 + n)/2
5) (Faap) A taxa de inscrição num clube de natação é de R$ 150,00 para o curso de 12 semanas. Se uma
pessoa se inscreve após o início do curso, a taxa é reduzida linearmente.
Expresse a taxa de inscrição em função do número de semanas transcorridas desde o início do curso:
resp: a
a) T = 12,50 (12 - x)
b) T = 12,50x
c) T = 12,50x -12
d) T = 12,50 (x + 12)
e) T = 12,50x + 12
6) (Puccamp) Durante um percurso de x km, um veículo faz 5 paradas de 10 minutos cada uma. Se a
velocidade média desse veículo em movimento é de 60 km/h, a expressão que permite calcular o tempo,
em horas, que ele leva para percorrer os x km é: resp: b
a) (6x + 5)/6 b) (x + 50)/60 c) (6x + 5)/120 d) (x/60) + 50 e) x + (50/6)
7) Examine cada relação e escreva se é uma função de A em B ou não. Em caso afirmativo determine o
domínio, a imagem e o contradomínio.
resp: a) R1 é uma função de A em B, D = A, Im = {0; 4; 16} b) não é função

9. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
9
8) Dados os conjuntos A = {-1; 0; 1; 2} e B = {-1; 0; 1; 2; 3; 4; 5}, faça o diagrama das relações abaixo, e
diga, qual delas é uma função A em B. resp: b
a) R1 = {(x;y) ∈ AxB/ y = x2
– 2 }
b) R1 = {(x;y) ∈ AxB/ y = 2x + 1 }
9) Dado o conjunto A = { -2; -1; 0; 1}, determine o conjunto imagem da função f: A→ℜ definida
por
f(x) = 1 – x2
. resp: Im = { -3; 0; 1}
10) Seja a função f: ℜ→ℜ definida por f(x)= x2
-10x+8. Calcular:
a) f(4) resp: -16
b) Os valores de x de modo que f(x)=-1. resp: 1 e 9
11) Dadas as funções f(x)=
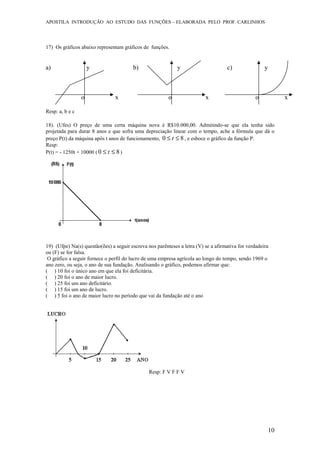
2
1
x + 1 e g(x) = x2
-1, calcule f(6)+g(-2). resp: 7
12) São dadas as funções f(x)= 3x+1 e g(x)=
5
4
x + a . Sabendo que f(1)-g(1)=
3
2
, calcule o valor de a .
resp: 38/15
13) Dada a função f: ℜ→ℜ definida por f(x)= ax + b, com a, b ∈ℜ, calcule:
a) a e b sabendo que f(1)=4 e f(-1)= -2; resp: a=3 e b=1
b) f(4). resp: 13
14) Dada a função f: ℜ→ℜ definida por f(x)= x2
-x-12, determine a de modo f(a+1) = 0.
resp: -4 ou 3
15)Encontrar o domínio das funções:
a) y=3x+4 resp: D=ℜ b) f(x)=x2
-3x+6 resp: D=ℜ c) f(x)=
4
93
+
+
x
x
resp: D=ℜ-{-4}
d) f(x) =
84
52
+
+
x
x
+
3
75
+
−
x
x
resp: D=ℜ-{-3;-2} e) f(x)=
81
10
2
−
−
x
x
-
7
35
+
−
x
x
resp: D=ℜ-{-9;-7;9}
f) f(x)= 63 −x resp: D={x∈ℜ/ x≥2} g) f(x)=
44
5
+x
+
4
102
+
−
x
x
resp: D={x∈ℜ/ x≥5}
16) Construa os gráficos das funções, e dê o domínio e a imagem:
a) f: A→B, definida por f(x) = x2
+1, sendo A={-1,0,1} e B={1,2,3,4}
b) f: A→B, definida por f(x) = 3x+1, sendo A=[-1,2] e B=[-4;8]
c) f: A→B, definida por f(x)=-4x, sendo A=]-2,1/2] e B= [-10,5]
resp:
a) y b) y c) y
7 ● ● 8
● 2 ●
1 ●
-1 o 1 x -1 0 2 x -2 0 x
● -2
-2 ●
D={-1,0,1} e IM={1,2} D=[-1,2] e IM=[-2,7] D=]-2,1/2] IM=[-2,8[

10. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
10
17) Os gráficos abaixo representam gráficos de funções.
a) y b) y c) y
o x o x o x
Resp: a, b e c
18). (Ufes) O preço de uma certa máquina nova é R$10.000,00. Admitindo-se que ela tenha sido
projetada para durar 8 anos e que sofra uma depreciação linear com o tempo, ache a fórmula que dá o
preço P(t) da máquina após t anos de funcionamento, 80 ≤≤ t , e esboce o gráfico da função P.
Resp:
P(t) = - 1250t + 10000 ( 80 ≤≤ t )
19) (Ufpe) Na(s) questão(ões) a seguir escreva nos parênteses a letra (V) se a afirmativa for verdadeira
ou (F) se for falsa.
O gráfico a seguir fornece o perfil do lucro de uma empresa agrícola ao longo do tempo, sendo 1969 o
ano zero, ou seja, o ano de sua fundação. Analisando o gráfico, podemos afirmar que:
( ) 10 foi o único ano em que ela foi deficitária.
( ) 20 foi o ano de maior lucro.
( ) 25 foi um ano deficitário.
( ) 15 foi um ano de lucro.
( ) 5 foi o ano de maior lucro no período que vai da fundação até o ano
Resp: F V F F V

11. APOSTILA INTRODUÇÃO AO ESTUDO DAS FUNÇÕES – ELABORADA PELO PROF. CARLINHOS
11
20) (Uff) O gráfico da função f está representado na figura:
Sobre a função f é FALSO afirmar que:
a) f(1) + f(2) = f(3)
b) f(2) = f(7)
c) f(3) = 3f(1)
d) f(4) - f(3) = f(1)
e) f(2) + f(3) = f(5) Resp: e
Prof. Carlinhos
Bibliografia:
Curso de Matemática – Volume Único
Autores: Bianchini&Paccola – Ed. Moderna
Matemática Fundamental - Volume Único
Autores: Giovanni/Bonjorno&Givanni Jr. – Ed. FTD
Contexto&Aplicações – Volume Único
Autor: Luiz Roberto Dante – Ed. Ática