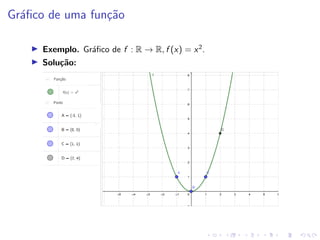
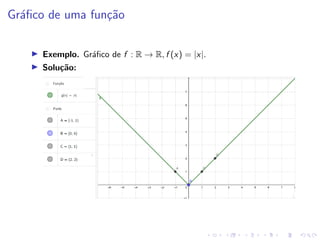
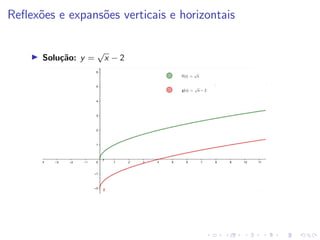
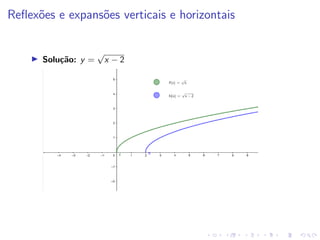
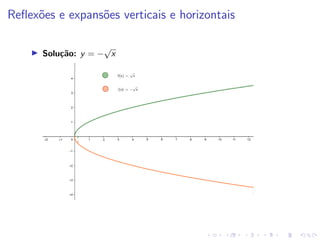
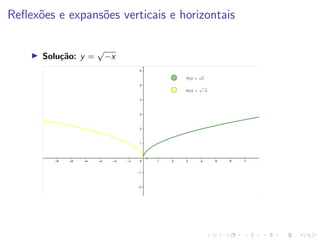
O documento descreve uma aula sobre funções matemáticas. Ele define funções, explica seus componentes (domínio e contradomínio) e fornece exemplos de diferentes tipos de funções, incluindo funções geradas por dados experimentais, modelos matemáticos, expressões polinomiais e outras. Além disso, discute como manipular funções através de deslocamentos, reflexões e expansões/contrações de seus gráficos.