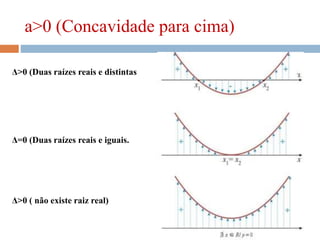
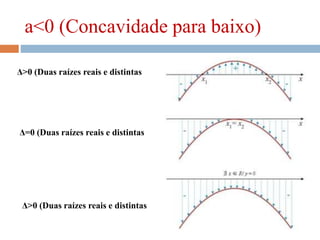
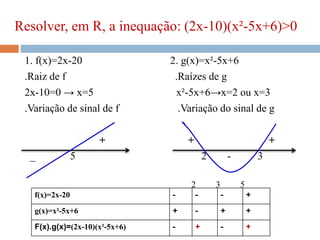
O documento discute inequações do 1º e 2º grau, definindo suas características e apresentando exemplos práticos. São abordadas regras para resolução envolvendo adição, subtração, multiplicação e divisão, bem como a determinação de soluções por meio de inequações. A bibliografia menciona diversas fontes de consulta relacionadas ao tema.

1. Inequações do 1º grau
Prof. : Zaqueu Oliveira

2. Inequações do 1º grau com uma incógnita
 Volume do paralelepípedo azul: 9.6.x=54x
 Volume do paralelepípedo verde: 5.4.4=80
 Volume do cubo vermelho: 8³=8.8.8=512
9cm
6cm
x
8cm
8cm
8cm
5cm
4cm
4cm

3. Definição
Inequações são sentenças matemáticas que possuem uma
ou mais incógnitas e são expressas por uma das
seguintes desigualdades: > (maior que), <(menor que), ≥
(maior ou igual a) e ≤ (menor ou igual a).
 Exemplos:
3x>9 2x≥x+3
3x maior que 9 2x maior ou igual a x mais 3
5x-2<8  -x≤12
5x menos 2 menor que 8 menor x menor ou igual a 12

4. Estudando as inequações
 Regras Práticas:
 Na Adição e Subtração por números positivos.
5>-7
5+1>-7+1
6>-6
 Na Multiplicação e Divisão por números
positivos.
5>-7
5.(2)>-7.(2)
10>-14

5. Estudando as inequações
 Regras Práticas:
 Na Multiplicação e Divisão por números
negativos.
5>-7
5.(-2)>-7.(-2)
-10<14

6. Exercicio
 Podemos determinar a medida x no
paralelepípedo azul resolvendo a inequação
54x +80>512.
54x +80>512
54x>512 – 80
54x>432
X>432/54
x>8
0 8

7. Bibliografia
 Slidesdare
 Google imagens
 Livro didático Vontade de saber de
matemática
 Artigos relacionados as inequações do 1º
grau.
 Infoescola.
 Só matemática

8. Inequação do 2º grau
 Prof:Zaqueu Oliveira

9. Definição
 Inequações são sentenças matemáticas que possuem uma
ou mais incógnitas e são expressas por uma das seguintes
desigualdades: Chama-se inequação do 2º grau toda
inequação que pode ser representada numa das seguintes
formas:
1. ax²+bx+c > 0
2. ax²+bx+c < 0
3. ax²+bx+c ≥ 0
4. ax²+bx+c ≤ 0
5. ax²+bx+c ≠ 0
Com {a,b,c} e a≠0.

10. a>0 (Concavidade para cima)
Δ>0 (Duas raízes reais e distintas
Δ=0 (Duas raízes reais e iguais.
Δ>0 ( não existe raiz real)

11. a<0 (Concavidade para baixo)
Δ>0 (Duas raízes reais e distintas
Δ=0 (Duas raízes reais e distintas
Δ>0 (Duas raízes reais e distintas

12. Resolver, em R, a inequação x²-2x-3>0
 Raízes da função f(x)=x²-2x-3
 Δ=b²-4.a.c → Δ=(-2)² - 4.(1).(-3)=16

 F(x)>0, então x<-1 ou x>3.

13. Resolver, em R, a inequação: (2x-10)(x²-5x+6)>0
1. f(x)=2x-20 2. g(x)=x²-5x+6
.Raiz de f .Raízes de g
2x-10=0 → x=5 x²-5x+6→x=2 ou x=3
.Variação de sinal de f .Variação do sinal de g
+ + +
_ 5 2 - 3
2 3 5
f(x)=2x-20
g(x)=x²-5x+6
F(x).g(x)=(2x-10)(x²-5x+6)

14. Conclusão
 O conjunto solução.

15. Bibliografia
 Slidesdare
 Google imagens
 Livro didático Vontade de saber de
matemática
 Artigos relacionados as inequações do 1º
grau.
 Infoescola.