O documento discute variáveis aleatórias contínuas, definindo-as como funções que assumem valores em um intervalo de números reais. Explica como atribuir probabilidades a variáveis contínuas usando funções de densidade de probabilidade, e como calcular medidas como média, variância e probabilidades para variáveis aleatórias contínuas usando integrais. Fornece exemplos ilustrativos sobre profundidade de lençol freático e tempo de teste.





![Vamos assumir que temos um instrumento ideal que não faz
aproximações. Nessas condições, podemos supor a sonda acoplada a
um instrumento indicador da profundidade e um dispositivo que,
quando a sonda encontrar água, provoque a imediata interrupção da
perfuração.
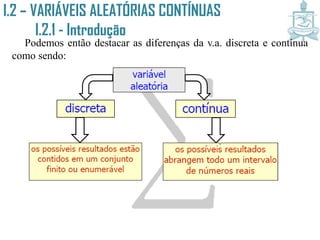
Uma vez não que temos informações adicionais a respeito da
profundidade do lençol, é razoável assumirmos que a sonda pode
parar em qualquer ponto entre 20 e 100 metros, sem que tenhamos
motivos para privilegiar essa ou aquela profundidade. Assim,
consideraremos todos os pontos como igualmente prováveis. Se
utilizarmos a mesma idéia de atribuir a cada possível ponto uma
probabilidade, teremos uma dificuldade extra, pois eles pertencem a
um intervalo de [20; 100], em que existem infinitos números reais.
I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.1 - Introdução](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-7-320.jpg)
![Assim, se cada um deles tiver, individualmente, probabilidade
maior que 0, a soma das probabilidades será igual a infinito e não 1,
como requer a definição da função de probabilidades. Em geral, em
situações como esta, não é interessante considerar um único valor
para a variável aleatória, mas intervalos de valores na atribuição de
probabilidades. Neste caso, sabemos que o espaço amostral
corresponde ao intervalo [20; 100] e as profundidades são
igualmente prováveis.
Suponha por um momento, que dividimos o espaço amostral em 8
intervalos de comprimento 10. Logo, é razoável atribuir aos
intervalos a probabilidade 1/8, correspondendo à relação entre o
comprimento de cada um deles e o comprimento do espaço amostral.
Isto é, 10 para 80 ou 1/8.
I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.1 - Introdução](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-8-320.jpg)
![I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.1 - Introdução
Assim, como dividimos em 8 faixas de igual comprimento e sem
intersecção entre elas, teremos os intervalos [20; 30), [30; 40), ...,
[90; 100] todos com a mesma probabilidade de 1/8, pois todos tem o
mesmo tamanho.
Para construirmos um histograma, podemos supor que 1/8 é a
frequência relativa da ocorrência de cada um dos intervalos. As
ordenadas do gráfico são as densidades, calculadas de modo que a
área de cada retângulo seja a frequência relativa (probabilidade) do
intervalo.](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-9-320.jpg)
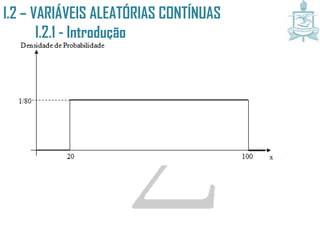
![I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.1 - Introdução
Note que, dada as características do problema, a divisão em 8 intervalos
produziu o mesmo valor de densidade de 1/80 pra todos eles. Se dividirmos
o intervalo [20; 100] em 16 faixas iguais, utilizando o mesmo argumento
anterior, temos que os intervalos [20; 25), [25; 30), ..., [95; 100] terão todos
a mesma probabilidade 1/16. O histograma correspondente será:](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-10-320.jpg)


![I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.2 – A função de densidade
probabilidade (fdp)Dizemos que f(x) é uma função contínua de probabilidade ou
função de densidade de probabilidade para uma variável aleatória
contínua X, se satisfaz duas condições:
i) 𝑓(𝑥) ≥ 0, para todo 𝑥 ∈ (−∞, +∞)
ii) A área definida por f(x) é igual a 1.
Com auxílio do cálculo diferencial e integral, podemos
caracterizar a condição ii) através de
Da mesma forma, para calcular probabilidades, temos que para
𝑎 ≤ 𝑏, , a integral indica a área sob f(x) definida
pelo intervalo [a; b].
.1)( dxxf
b
a
dxxfbXaP ;)()(](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-15-320.jpg)
![I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.2 – A função de densidade
probabilidade (fdp)Note que, pela forma como a atribuímos as probabilidades no
caso contínuo, teremos área zero sob qualquer valor individual, isto
é, P(X = k) = 0 para qualquer k. Portanto, em se tratando de variáveis
aleatórias contínuas, a probabilidade de ocorrência de um valor
isolado é sempre zero e, consequentemente, as probabilidades
calculadas sobre os intervalos [a; b], [a; b), (a; b] e (a; b) são as
mesmas, para qualquer valor de a e b.
Exemplo: Num teste intelectual com alunos de um colégio Y, o
tempo para realização de uma bateria de questões de raciocínio
lógico é medido e anotado para ser comparado com um modelo
teórico. Este teste é utilizado para identificar o desenvolvimento da
capacidade de raciocínio lógico e auxiliar a aplicação de medidas
corretivas. O modelo teórico considera T, tempo de teste em minutos,
como uma variável aleatória contínua com função de densidade de
probabilidade dada por:](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-16-320.jpg)
![O gráfico da fdp é apresentado a seguir (construiremos ele no
software R). Deve ser notado que, pela definição de f(x), ela se
anula para t < 8 ou t >15.
Vamos verificar agora se a função f(t) satisfaz a definição de
densidade. Para calcular P(9 < T 12), vamos obter a área sob f(t)
no intervalo (9; 12]:
contráriocaso
tse
tset
tf
0
1510
20
3
;108)4(
40
1
)(
I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.2 – A função de densidade
probabilidade (fdp)](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-17-320.jpg)
![Assim P(9< T 12) = 7/16 valor esse obtido pela soma do
trapézio definido no intervalo (9, 10) com o retângulo determinado
pelo intervalo [10,12] (veja a figura).
6 8 10 12 14 16 18
0.000.050.100.15
t
f(t)
I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.2 – A função de densidade
probabilidade (fdp)](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-18-320.jpg)






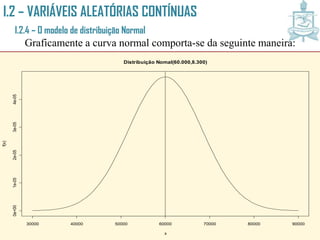

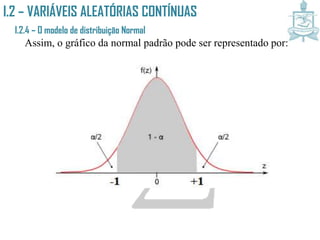
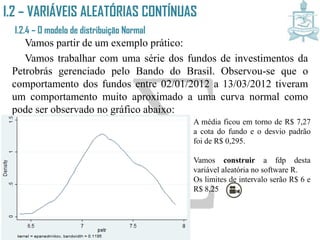


![I.2 – VARIÁVEIS ALEATÓRIAS CONTÍNUAS
I.2.4 – O modelo de distribuição Normal
Aplicações da v.a. reduzida.
A transformação da normal para a sua correspondente reduzida
z~N(0,1). Para determinar a probabilidade de X [a,b], procedemos
com o seguinte cálculo:
P(a X b) = P(a - X - b - ) =
e, portanto, quaisquer que sejam os valores de e , utilizamos a
Normal Padrão para obter probabilidades com a distribuição Normal.
b
Z
a
P
bXa
P](https://image.slidesharecdn.com/02-variveisaleatriascontnuasi-140411150910-phpapp02/85/Variaveis-aleatorias-continuas-Estatistica-II-31-320.jpg)