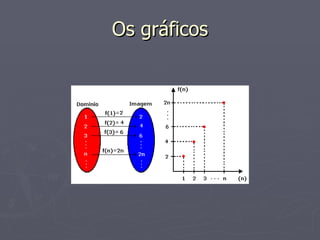
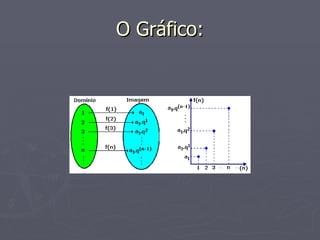
O documento discute diferentes tipos de funções e sequências, incluindo: 1) Funções reais, vetoriais e matriciais; 2) Sequências reais finitas e infinitas; 3) Progressões aritméticas finitas e suas propriedades como razão, termo geral e termos eqüidistantes.