1) O documento apresenta conceitos fundamentais de álgebra, como porcentagem, potenciação, radiciação e fatoração. 2) Também aborda sequências numéricas, como progressão aritmética e progressão geométrica. 3) Por fim, discute noções básicas de geometria plana, incluindo relações métricas, teoremas e fórmulas para cálculo de áreas.

1. TURMA DO M˘RIO
Álgebra
Porcentagem
Taxa percentual ou porcentagem de um número a sobre um número b, b ≠ 0 é a razão
x x a x
tal que: = , e se indica: = x% .
100 100 b 100
A palavra porcentagem deriva de por (dividido) e centagem (100). Quando se fala x % de
x
um número, significa multiplicar este número por .
100
15
Exemplo: 15 % de 200 = . 200 = 30 .
100
Potenciação
Definições
∀ a ∈ R ⇒ a0 = 1
∀ a ∈ R e ∀ n ∈ N ⇒ a n = a n−1 . a
Propriedades
1. a m . a n = a m+n
am
2. n = a m−n , a ≠ 0
a
3. (a m ) n = a m . n
4. (a . b) n = a n . b n
5. (a : b)n = an : bn , b ≠ 0
1
6. a – n = n , a ≠ 0
a
( m)
n n
Nota: Em geral a ≠ am
Em geral (a + b) ≠ a n + b n
n
Radiciação
Propriedades
1. n
a .b=na . n b
2. n
a : b = n a : n b ,b ≠ 0
( a)
m
3. n
= n am
4. m n
a = n .m a
m
5. n
am = a n
n .p
6. am . p = n am
www.turmadomario.com.br -1

2. Produtos notáveis
(a + b) × (a – b) = a2 - b2
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a – b)3 = a3 – 3a2b + 3ab2 – b3
(a + b + c)2 = a2+ b2 + c2 + 2 × (ab + ac + bc)
Fatoração
ab + ac = a × (b + c)
ab + ac + db + dc = a × (b + c) + d × (b + c) = (b +c) × (a + d)
a2 + 2ab + b2 = (a + b)2
a2 – 2ab + b2 = (a – b)2
ax2 + bx + c = a.(x – a1) × (x – a2), onde a1 e a2 são as raízes de ax2 + bx + c = 0.
a3 + 3a2b + 3ab2 + b3 = (a + b)3
a3 – 3a2b + 3ab2 – b3 = (a – b)3
a3 + b3 = (a + b) × (a2 – ab + b2)
a3 – b3 = (a – b) × (a2 + ab + b2)
a2 + b2 +c2 + 2 × (ab + ac + bc) = (a + b + c)2
Números naturais
Números primos: Um número natural e maior que 1 é primo se ele tiver apenas dois
divisores naturais distintos: 1 e ele mesmo.
Números primos entre si: Dois números naturais são primos entre si se o único divisor
natural comum entre eles for 1.
Quantidade de divisores naturais de um número natural
Se n = ap.bq.cr.ds..., então n tem (p+1) × (q+1) × (r+1)... divisores positivos, sendo n um
número natural e a, b, c, d, ... fatores primos do número n.
Seqüências
Definições
Seqüência real é toda função f : I ® R, onde I = N* ou I = {1, 2, 3, ... ..., n}
Se I = N*, a seqüência é chamada infinita.
Se I = {1, 2, 3, ... ..., n} , a seqüência é chamada finita.
2

3. Progressão Aritmética (PA)
Definição
Progressão aritmética (PA) é toda seqüência numérica onde, a partir do primeiro termo
encontramos os demais somando ao anterior um valor fixo r chamado de razão da PA.
Conseqüência da definição: r = a2 – a1 = a3 – a2 = a4 – a3 = ... ... = a n+1 – a n = r
Classificação das PA´s
Uma PA de números reais pode ser:
I.crescente: (razão positiva): r >0 Þ a n+1 > a n
II. decrescente (razão negativa): r < 0 Þ a n+1 < a n
III. constante (razão nula): r = 0 Þ a n+1 = a n
Fórmula do termo geral de uma PA
Seja a PA(a1, a2, a3, ... ... an). Então: an = a1 + (n – 1) × r, n Î N*
Conseqüência: Para obtermos um termo qualquer an, a partir de um termo de ordem p
(ap), poderemos utilizar a regra:
an = ap + (n – p) × r, n,p Î N*
Termos eqüidistantes em PA
Na PA genérica: PA(a1, a2, a3,... ..., ap-1, ap, ap+1,... ...,an), tem-se:
a p -k + a p + k
ap = com p, k Î IN*
2
Soma dos n primeiros termos de uma PA
Seja a PA(a1, a2, a3,... ..., an,......) , a soma de seus n primeiros termos é dada por:
(a 1 + a n ) × n
Sn =
2
3

4. Progressão Geométrica (PG)
Definição
Progressão geométrica (PG) é toda seqüência em que cada termo, a partir do segundo, é
igual ao produto do termo anterior por uma constante q, que é chamada razão da P.G.
Conseqüência da definição:
a n+ 1
Se an ¹ 0, então q = ; ou seja, encontramos a razão da PG dividindo um termo
an
qualquer pelo seu antecessor.
Classificação das PG´s:
Uma PG pode ser:
I.Crescente: quando an+1 > an
Exemplo: PG(1, 2, 4, 8, 16, ...), q = 2
II. Decrescente: quando an+1 < an
Exemplo: PG(81, 27, 9, 3, 1, ...), q = 1/3
III. Constante: quando an+1 = an
Exemplo: PG(2, 2, 2, 2, 2, ...), q = 1
IV.Alternante: quando a1 ¹ 0 e q < 0
Exemplo: PG(2, – 4, 8, – 16, 32, ...), a1 = 2 e q = –2
V. Não decrescente: quando a1 < 0 e q = 0
Exemplo: PG(– 2, 0, 0, 0, 0, ...), a1 = – 2 e q = 0
VI.Não crescente: quando a1 > 0 e q = 0
Exemplo: PG(5, 0, 0, 0, 0, ...), a1 = 5 e q = 0
Fórmula do termo geral da PG
n–1
Seja a PG genérica: PG(a1, a2, a3, a4, ......). Assim: an = a1 × q , n Î N*
Conseqüência: Para obtermos um termo qualquer an, a partir de um termo de ordem p
(ap), poderemos utilizar a regra: an = ap × qn – p, n,p Î N*
Termos eqüidistantes em PG
Na PG genérica: PG(a1, a2, a3,... ..., ap-1, ap, ap+1,... ...,an), então:
(ap)2 = (ap – k) × (ap + k), p,k Î N*
Produto dos n primeiros termos de uma PG (Pn)
Seja a PG(a1, a2, a3, ..., an, ..., .... ) indicaremos por Pn o produto de seus n primeiros
n(n-1)
× n
n
termos. Assim: Pn = a1 ×q 2 ou Pn = (a1 × an) 2
4

5. Soma dos n primeiros termos de uma PG (Sn)
Seja (a1, a2, a3, ..., an, ...) uma PG de razão q e indiquemos por Sn a soma de seus n
primeiros termos. Assim:
a 1 × (qn - 1)
Se a PG não for constante, ou seja q ¹ 1 teremos: Sn =
q -1
Se a PG for constante, ou seja q = 1 teremos: Sn = n × a1
Soma dos termos de uma PG infinita (S)
Seja a P.G. = (a1, a2, a3, . . . , an, . . . ) de razão q e a soma de seus infinitos termos
Sn = a1 + a2 + a3 + . . . + an + . . . (série)
Quando lim S n = S existe e é finito, dizemos que a série converge para S.
n®¥
Quando esse limite não existe ou não é finito dizemos que a série diverge (não se pode
a1
determinar tal soma). Se – 1 < q < 1, pode-se demonstrar que: lim S n = S =
n®¥ 1- q
Função Exponencial
f(x) = ax ; a>0 e a¹1 Imf = IR *
+
Df = IR
y y
a>1 0<a<1
função crescente função decrescente
1
0 x 0 x
Propriedades de potência
1. am . an = am + n
2. am : an = am – n , a ¹ 0
3. (am)n = am .n
4. n a m = a m n , n Î IN / n >1
1
5. a– n = , a ¹ 0
an
5

6. Equação exponencial
af(x) = ag(x) Û f(x) = g(x)
Inequação exponencial
af(x) > ag(x) Û f(x) > g(x), se a >1
af(x) > ag(x) Û f(x) < g(x), se 0 < a < 1
Logaritmo
Definição
logba = x Û a = bx com a > 0, 0 < b ¹ 1
Propriedade de logaritmo
1. logc (a.b) = logca + logcb; a > 0, b > 0, 0 < c ¹ 1
2. logc æ ö = logca – logcb; a > 0, b > 0, 0 < c ¹ 1
a
ç ÷
è bø
3. logc am = m . logca; a > 0, 0 < c ¹ 1 e m Î IR
1
4. logcm a = . logca; a > 0, 0 < c ¹ 1 e m Î IR*
m
Função Logarítmica
f(x) = logax , a > 0 e a ¹ 1 Imf = IR
Df = IR *
+
y y
0 1 x 0 1 x
a>1 0<a<1
função crescente função decrescente
6

7. Geometria Plana
Relações métricas no triângulo retângulo
h2=m × n b × c=a × h
b h c b2=a × m a2=b2 + c2 (Pitágoras).
m n c2=a × n
a
Relações métricas no círculo
P B
A
A B
P D C A
C
B P
D T
PA × PB = PC × PD PA × PB = PC × PD (PT)2 = PA × PB
Lei dos
a b c
= = = 2R
sena senb seng
Lei dos cossenos
a2 = b2 + c2 – 2 × b × c ×cos a
b2 = a2 + c2 – 2 × a × c ×cos b
c2 = a2 + b2 – 2 × a × b ×cos g
7

8. Teorema de Tales
a1 // a2 // a3 // .....
AB BC CD AC AD
= = = =
A' B' B' C' C' D' A' C' A' D'
Teorema da bissetriz interna
A
b c
x y b c
=
S x y
Teorema da bissetriz externa
A
b c
c
y
C S
B
b c
x =
x y
Semelhança de triângulos
A
P
b
H c y
h z
B C Q R
a x
a b c H Área DABC
= = = =k = k2
x y z h Área DPQR
8

9. Arcos e ângulos
a a+b
a=a a= a=
2 2
b
a–b a
a= a=
2 2
Razões trigonométricas
b c
sen a = sen b =
a a
c b
cos a = cos b =
a a
b c
tg a = tg b =
c b
Comprimento da circunferência
R
C = 2pR
Base média de triângulo
« «
MN // BC
BC
MN =
2
9

10. Base média de trapézio
« «
MN // AB
AB+ CD
MN =
2
Baricentro de triângulo
Polígonos convexos
Sendo n = número de lados;
d = número de diagonais;
Si = soma dos ângulos internos e
Se = soma dos ângulos externos,
n(n – 3)
temos: d= Si = (n – 2) × 180ºe Se = 360º
2
Áreas
Retângulo Quadrado Paralelogramo
Triângulo Trapézio
10

11. Losango 1 Losango 2
(AC) × (BD)
B A Los =
2
C
Fórmulas especiais para área do triângulo
l2 3 b×c
A= A= A = p(p – a) × (p – b)(p – c)
4 2
a +b +c
em que p =
2
1 a ×b×c
A= × a × b × sena A=rp A=
2 4R
a +b +c
p=
2
Círculo
R
A = p ×R2
Setor circular
a ×p ×R2 a ×R2 l ×R
A= A= A=
360º 2 2
a em radianos
11

12. Análise Combinatória / Probabilidades
æ nö n! æ combinação de n objetos distintos ö
Número binomial: ç ÷ =
ç p ÷ p!(n – p)! = C n, p = ç agrupados de p em p
ç ÷
÷
è ø è ø
æ nö æ nö æ nö n æ nö
Teorema binomial: (a + b)n = ç ÷ anb0 + ç ÷ an – 1b1 +. . .+ ç ÷ a0bn = å ç ÷ a n–i bi
ç0÷ ç 1÷ ç n÷ ç ÷
è ø è ø è ø i =o è i ø
n!
Arranjo: An, p = Þ n objetos distintos seqüenciados (enfileirados) de p em p
(n – p)!
Permutação de n objetos distintos: Pn = n!
n! a objetos iguais entre si
Permutação de elementos repetidos: Pna, b, g = ,
a!b!g! b objetos iguais entre si
g objetos iguais entre si
n.o de elementos do conjunto evento n(A)
Probabilidade de ocorrer um evento = = = P(A)
n.o de elementos do espaço amostral n(E)
æ probabilidade de ocorrer ö æ ocorrer o ö
ç
ç o evento A ÷ e em seguida ç
÷ ç evento B ÷=
÷
è ø è ø
æ probabilidade de ö
æ probabilidade de ö ç ÷
=ç
ç ocorrer o evento A ÷ x ç ocorrer o evento B
÷ ÷ Þ Teorema da multiplicação
è ø ç sabendo que A ocorreu ÷
è ø
Exemplo:
2 bolas azuis æ tirar uma bola azul e em ö 2 1
5 bolas verdes ç seguida uma bola azul ÷ = 7 ´ 6
Pç ÷
è ø
chance de retirar uma
bola azul sabendo que
já saiu uma azul
Conjuntos, Funções e Inequações
Relação
Considerando dois conjuntos A e B, não-vazios, chamamos relação (binária) de A e B a
qualquer subconjunto do produto cartesiano ( A x B = {(x; y) / x Î A Ù x Î B}).
Definição
Uma relação f de A em B é uma função de A em B, se, para todo x Î A, existe um único y
Î B tal que (x; y) Î f. (Indica-se: f : A ® B).
12

13. Exemplo Contra-exemplo
A B A B · Domínio de f = D(f) = A = {1, 2, 5}
f g
1 3 1 4 · Conjunto Imagem de f = Im(f) = {3, 4}
2 4 2 5 · Contradomínio = CD(f) = B = {3, 4, 6}
5 6 3 6
· 4 é imagem de 5, isto é, 4 = f(5)
f é função g não é função · 4 é imagem de 2, isto é, 4 = f(2)
Tipos de função
Função crescente e decrescente
· Uma função f é crescente em A Ì Df Û (x1 < x2 Þ f(x1) < f(x2), " x1, x2 Î A).
· Uma função f é decrescente em A Ì Df Û (x1 < x2 Þ f(x1) > f(x2), " x1, x2 Î A).
Função injetora, sobrejetora e bijetora
· Uma f : A ® B é injetora se todos os elementos distintos em A têm imagens distintas em
B (" x1, x2 Î A, x1 ¹ x2 Þ f(x1) ¹ f(x2)).
· Uma f : A ® B é sobrejetora se todos os elementos de B são imagens de elementos de A
(Im(f) = CD(f) ou " y Î B, $ x Î A / f(x) = y)
· Uma função de f : A ® B é bijetora se é injetora e sobrejetora.
Exemplos:
A B A B A B A B
f f f f
1 4 1 4 3 1 1 4
2 5 3 3 4 2 2 5
3 5 2 6 3 3 6
1
f é sobrejetora f é injetora f é bijetora f não é injetora
e não é injetora e não é sobrejetora e nem sobrejetora
Função par e ímpar
· Uma função f : A ® B é par Û " x Î A, f(x) = f( – x).
· Uma função f : A ® B é ímpar Û " x Î A, f(x) = – f( – x).
Função periódica
· Uma função f : A ® B é periódica de período p Û " x Î A, f(x + p) = f(x), p > 0.
Função composta
· Dadas duas funções f e g, podemos obter uma outra função fog, tal que
fog(x) = f(g(x)), chamada função composta de f com g.
13

14. Função inversa
· Denomina-se inversa da função bijetora y = f(x), f : A ® B a função f– 1: B ® A, tal que
f–1 (y) = x.
Observação:
Para se obter a inversa de uma função f (bijetora) definida por uma sentença matemática
y = f(x)
a. troca-se x por y e y por x;
b. coloca-se o novo y em função do novo x.
Matrizes, Determinantes e Sistemas Lineares
Propriedades dos determinantes
a. det(At) = det(A).
b. Se uma linha (ou coluna) é formada só de zeros, o determinante é igual a zero.
c. Quando trocamos de lugar duas linhas (ou colunas) paralelas, o determinante fica
multiplicado por –1.
d. Se duas linhas (ou colunas) paralelas são iguais (ou proporcionais), o determinante é
igual a zero.
e. Se os elementos de uma linha (ou coluna) apresentam um fator comum k, este pode ser
colocado em “evidência”.
f. Se A é uma matriz quadrada de ordem n, então det(k.A) = kn.det(A)
g. Teorema de Binet: det(A.B) = det(A).det(B)
Atenção: em geral, det(A+B) ¹ det(A) + det(B)
h. Teorema de Jacobi (importante para obtenção de zeros). O determinante de uma
matriz não se altera quando somamos a uma linha (ou coluna) outra linha (ou coluna)
paralela multiplicada por uma constante.
é1 0 0 0ù
ê –3 4 0 0ú
i. Matriz Triangular: A = ê ú Þ det(A) = 1× 4(–5) × 8
ê2 3 –5 0ú
ê5 6 7 8ú
ë û
Multiplicação de matrizes
æ a bö æ x y ö æ ax + bz ay + bw ö
ç c d ÷ × ç z w ÷ = ç cx + dz cy + dw ÷
ç ÷ ç ÷ ç ÷
è ø è ø è ø
a. Todo sistema de equações lineares apresenta apenas uma solução, ou seja, é um
sistema possível e determinado (s. p. d.), quando D ¹ 0, onde D é o determinante da
matriz dos coeficientes de tal sistema.
b. Para os casos onde D = 0, para analisar o sistema, ou seja, dizer se o mesmo é
impossível (s. i.) ou indeterminado (s. p. i.), deve-se escalonar tal sistema, eliminando
ordenadamente as incógnitas das equações.
A equação, na incógnita x, ax = b tem apenas uma solução para a ¹ 0; tem infinitas
soluções para a = 0 e b = 0 e não tem solução para a = 0 e b ¹ 0.
14

15. Trigonometria
kp ö
Relações Fundamentais Conseqüências æ x ¹
ç ÷
è 2 ø
1
sen2x + cos2x = 1, "x Î R cotgx =
tgx
senx æ p ö
tgx = ç x ¹ + kp ÷ 1 + tg2x = sec2x
cosx è 2 ø
cosx
cotgx = ( x ¹ kp) 1 + cotg2x = cossec2x
senx
1 æ p ö 1
secx = ç x ¹ + kp ÷ cos 2 x =
cosx è 2 ø 1+ tg2 x
1 tg2 x
cossecx = ( x ¹ kp ) sen2 x =
senx 1+ tg2 x
Fórmulas de adição
cos(a + b) = cos a . cos b – sen a . sen b
cos(a – b) = cos a . cos b + sen a . sen b
sen(a + b) = sen a . cos b + sen b . cos a
sen(a – b) = sen a . cos b – sen b . cos a
tg a + tg b
tg(a + b) =
1– tg a × tg b
tg a – tg b
tg(a – b) =
1+ tg a × tg b
Fórmulas de multiplicação
Arcos duplos Arcos Triplos
sen 2a = 2 sen a cos a sen 3a = 3 sen a – 4 sen3 a
ìcos 2 a – sen2 a cos 3a = 4 cos3 a – 3 cos a
ï
ï ou 3 tga – tg3 a
ï tg 3a =
cos 2a = í 2cos 2 a – 1 1– 3tg2 a
ï ou
ï 2
ï
î 1– 2sen a
2 tg a
tg 2a =
1– tg2 a
15

16. Fórmulas de divisão
x 1– cos x x 1+ cos x x 1– cos x
sen = ± cos = ± tg = ±
2 2 2 2 2 1+ cos x
Fórmulas de transformação em produto
p+ q p– q
cos p+ cos q = 2 × cos × cos
2 2
p+ q p– q
cos p – cos q = –2 × sen × sen
2 2
p+ q p– q
sen p+ sen q = 2 × sen × cos
2 2
p– q p+ q
sen p – sen q = 2 × sen × cos
2 2
sen(p+ q)
tg p+ tg q =
cos p × cos q
sen(p – q)
tg p – tg q =
cos p × cos q
Equações trigonométricas fundamentais
sen a = sen b Þ a = b+ 2kp ou a = (p – b) + 2kp
cos a = cos b Þ a = ±b + 2kp
tg a = tg b Þ a = b+ kp
Funções circulares inversas
p p
y = arc senx Û seny = x e – £y£
2 2
y = arc cosx Û cosy = x e 0 £ y £ p
p p
y = arc tgx Û tgy = x e – <y<
2 2
16

17. Geometria Espacial
· O volume de um prisma e o de um cilindro (retos ou oblíquos) é igual ao produto da
área da base (B) pela altura (H). E o volume de uma pirâmide e o de um cone reto (ou
oblíquo) é igual a 1/3 do produto da área da base pela altura.
R
H H g
H H
B B R
V = BH 1
V = — BH
3
· Planificando a superfície lateral de um cilindro reto de raio R e altura H obtemos um
retângulo de lados 2pR e H. Então a área lateral (AL) do cilindro reto é:
· Planificando a superfície lateral de um cone reto de raio R e geratriz g obtemos um setor
circular de raio g e arco 2pR. Então a área lateral do cone reto é.
2pR × g
AL = Asetor Þ AL = Þ AL = pRg
2
Sendo a a medida, em graus, do setor,
temos:
2pR × g a a
Asetor = = pg2 Þ R = g
2 360º 360º
· O volume V e a área A de uma esfera de raio R são dados por:
4 3
R A = 4 pR2 e V= pR
3
17

18. Números Complexos
Forma algébrica
Nomenclatura
z = a + bi (a, b Î IR)
i = unidade imaginária
a = Re (z) = parte real de z
b= Im (z) = coeficiente da parte imaginária de z
Exemplos de números complexos
z = 3i = 0 + 3i = número imaginário puro.
z = – 6 = – 6 + 0i = número real.
z = a + bi (b ¹ 0) = número imaginário ou número complexo não real.
Potências inteiras de i (ik, k Î ZZ )
i0 = 1 e i4k = 1
i1 = i e i4k+1 = i4k . i1 = i
i2 = – 1 e i4k+2 = i4k . i2 = – i
i3 = – i e i4k+3 = i4k . i3 = – i
Conjugado de z = a + bi (a, b Î IR)
z = a – bi
Propriedades
1. z + w = z + w
2. z . w = z . w
3. æ ö =
z z
ç ÷
èwø w
4. z n = ( z ) n (n Î ZZ)
5. ( z ) = z
Produtos e divisões notáveis
1. (1 + i)2 = 2i
2. (1 – i)2 = – 2i
3. (1+ i)(1 – i) = 2
1+ i
4. =i
1– i
1– i
5. =–i
1+ i
18

19. Igualdade na forma algébrica
a + bi = c + di Û a=c e b=d (a, b, c, d Î IR)
Representação no plano de Argand-Gauss
z = a + bi = (a, b) = P (a, b Î IR)
P = afixo de z
dop = |z| = a 2 + b2 = módulo de z
q + k . 2p = arg(z) = argumento de z
0
(0 £ q < 2p)
q = argumento principal de z
Propriedades
1. | z |2 = z . z
2. |z . w | = | z | . | w |
z z
3. = (w ¹ 0)
w w
4. | z n | = | z | n , n Î ZZ
5. | z + w | £ | z | + | w |
6. | z | = | z |
Forma trigonométrica de z Î C*
z = a + bi = | z | (cos q + isen q )
ìcos q = a
ï
ï z
| z | = a 2 + b2 e í
b
ïsen q =
ï
î z
Igualdade na forma trigonométrica
|z|( cos q + i sen q ) = |w|( cos a + i sen a )
1444 444 2 3 144424443
z w
z=w Û |z| = |w| e
kÎZZ
q = a + k . 2p
19

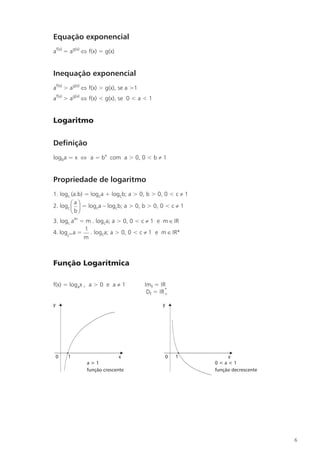
20. Operações na forma trigonométrica
Sejam z = |z| (cos q + isen q )
z1 = |z1| (cos q 1 + isen q 1)
z2 = |z2| (cos q 2 + isen q 2 )
· Multiplicação
z1 . z2 = |z1| . |z2| . [cos (q1 + q2) + isen (q1 + q2)]
· Divisão
z 1 |z 1|
= [cos (q1 – q2) + isen (q1 – q2)]
z 2 |z 2|
· Potenciação
zn = |z|n . [cos (n q) + isen (nq)]
· Radiciação
é q 2p q 2p ù
z = w k = n z êcos æ + k × ö + i senæ + k × ö ú ,
n C
ç ÷ ç ÷ (k = 0, 1, 2, . . . , n – 1)
ë èn n ø èn n øû
Propriedades
1. w0 + w1 + w2 + . . . + wn – 1 = 0
2. A raiz enésima de z divide a circunferência em n partes iguais.
3. O raio dessa circunferência é n | z |.
q 2p
4. O “ponto de partida” (wo) é o arco e o “pulo’ de uma raiz para outra é de .
n n
Equação binômia em C
axn + b = 0 (a ¹ 0)
C
–b –b
axn = – b Þ xn = Þ x =n = wk , (k = 0, 1, 2, . . . , n – 1)
a a
Geometria Analítica
Distâncias
De dois pontos A e B
d AB = (x B – x A ) 2 + (y B – y A ) 2
Do ponto P à reta (r) ax + by + c = 0
|ax P + by P + c|
d=
a 2 + b2
20

21. Pontos especiais
a.
AM
M divide AB na razão =r
MB
xM – x A y – yA
r= = M
xB – xM yB – yM
æ x + xB y A + yB ö
Se M é ponto médio de AB, M = ç A , ÷
è 2 2 ø
b. Ponto do eixo x: A = (a, 0)
Ponto do eixo y: B = (0, b)
Ponto da bissetriz dos quadrantes pares: C = (k, k)
Ponto da bissetriz dos quadrantes ímpares: D = (k, – k)
æ x + xB + xC y A + yB + yC ö
Baricentro do DABC: G = ç A , ÷
è 3 3 ø
Área do DABC
xA yA 1
|D|
S= onde D = x B yB 1
2
xC yC 1
Observação: Se A, B e C são colineares, D = 0.
Equação de circunferência
(x – xC)2 + (y – yC)2 = r2
Centro C e raio r, equação reduzida.
Equação de reta
· Geral: ax + by + c = 0 (r)
xA yA 1
Conhecendo 2 pontos A e B de r: x B yB 1 =0
x y 1
· Reduzida: y = mx + k
m... coeficiente angular de r
k.... coeficiente linear de r
m = tga (não existe, se m é vertical)
yB – y A
Conhecendo 2 pontos A e B da reta, m =
xB – x A
21

22. Paralelas / perpendiculares
· r // s Û mr = ms
Exemplos:
Paralela a y = 2x – 3 é y = 2x + k
Paralela a 2x + 5y – 3 é 2x + 5y + k = 0
· r ^ s Ûmr . ms = – 1
Exemplos:
2 3
Perpendicular a y = x – 3 é y = – x + k
3 2
Perpendicular a 2x + 5y – 6 = 0 é 5x – 2y + k = 0
Observação:
Se P pertence a ax + by + c = 0, então axP + byP + c = 0.
22