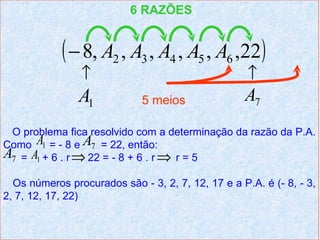
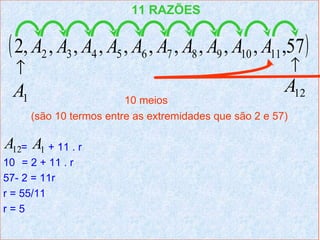
O documento aborda conceitos fundamentais sobre progressões aritméticas, incluindo definições de sequência numérica, término, e razão. Exemplos práticos são apresentados para ilustrar a determinação de termos, somas e interpolação de sequências. Além disso, são fornecidos exercícios para praticar a aplicação das fórmulas e conceitos discutidos.

1. PROGRESSÕES ARITMÉTICAS

2. AO FINAL DESTA AULA SERÁ IMPORTANTE
ENTENDER:
 Conjunto dos números reais.
 O que é uma sequência numérica?
 Como determinar uma sequência finita ou infinita?
 Como determinar os termos de uma sequência?
 O que é uma sucessão aritmética e soma dos termos de uma
P.A.?

3. O QUE É UMA SEQUÊNCIA NUMÉRICA?
São elementos cujos números pertencem ao conjunto
dos números reais, esses elementos estão dispostos
em uma certa ordem, um conjunto assim é chamado de
sequência numérica.
Quando uma sequência tem infinitos termos ela se
chamara infinita; caso contrário, é uma sequência finita.

4. EXEMPLOS
Sequências infinitas:
Sucessão dos números pares (2, 4, 6, 8 ,...)
Sucessão dos números impares (1, 3, 5, 7,...)
Sequências finitas:
Sucessão dos números (1, 2, 3, 4, 5)
Sucessão dos números (10, 20, 30, 40, 50)

5. O QUE É UMA PROGRESSÃO ARITMÉTICA?
É toda sequência numérica na qual, a partir do
segundo, cada termo é igual à soma de seu
antecessor com uma constante chamada de
razão, essa constante é indicada pela letra r.

6. DETERMINAÇÃO DE UMA SEQUÊNCIA
Determinar uma sequência é saber qual a imagem de
n para todo n ∈ *
lN , e podemos fazê-lo aplicando a lei
de recorrência ou o termo geral.
O que é lei de recorrência?
É uma lei que permite calcular cada termo da
sequência, apartir do termo anterior.

7. É necessário também, para determinação da
sequência, que o primeiro termo seja dado.
 A1 = 5

 An +1 = n + 1
Logo : A1 = 5
A2 = n + 1 ⇒ A2 = A1 + 1 ⇒ A2 = 5 + 1 ⇒ A2 = 6
A3 = n + 1 ⇒ A3 = A2 + 1 ⇒ A3 = 6 + 1 ⇒ A3 = 7
A4 = n + 1 ⇒ A4 = A3 + 1 ⇒ A4 = 7 + 1 ⇒ A4 = 8
A5 = n + 1 ⇒ A5 = A4 + 1 ⇒ A5 = 8 + 1 ⇒ A5 = 9

8. Onde :
A1 é o primeiro termo.
A2 é o segundo termo.
A3 é o terceiro termo.
A4 é o quarto termo.
A5 é o quinto termo.

9. EXEMPLOS
• (-5, -3, -1, 1, 3, 5, 7,...) é P.A. de razão r = 2.
• (8, 8, 8, 8, 8, 8, 8, 8,...) é P.A. de razão r = 0.
• (20, 16, 12, 8, 4, 0) é P.A. de razão r = -4.
Então uma P.A. pode ser:
Crescente: quando r é maior que zero (r > 0).
Constante: quando r é igual a zero (r = 0).
Decrescente: quando r é menor que zero (r < o).

10. AGORA VAMOS ALGUNS EXEMPLOS DE
EXERCÍCIOS
Exemplo 1: Escreva os quatro primeiros termos de uma P.A
sabendo que:
A1 = -3 e r = 4. r= A2 - A1
A2 = A1 + r ⇒ A2 = -3 + 4 = 1
A3= A2 + r⇒ A3 =1 + 4 = 5
A4= A3 + r⇒ A4 = 5 + 4 = 9
A5= A4 + r⇒ A5 = 9 + 4 = 13

11. Exemplo 2: Escreva uma P.A. de cinco termos sabendo que:
A1= 2 e r = 3.
A2 =A1 + r ⇒ A2 = 2+ 3
A3= A2 + r ⇒ A3 = 2 + 6
A4 = A3 + r ⇒ A4 = 2 + 9
A5
A5 = A4 + r ⇒ 2= + 12

12. FÓRMULA DO TERMO GERAL DE UMA P.A.
Determinar o termo geral de uma P.A. é calcular o valor de uma
termo A n qualquer. Essa fórmula permite que encontremos,
dados três dos quatro elementos.
Sendo:
An ⇒ termo geral
n ⇒ números de termos
A1 ⇒ primeiro termo
r ⇒ razão

13. Questão 1: Calcule A20 na P.A.: (2, 5, 8,...)
An= A1 + (n – 1). r
An = A20
A20 = 2 + (20 – 1). 3
A1 = 2
A20= 2 + 19. 3 n = 20
A20= 2 + 54 r=3
onde
A20 = 59
r = A2 − A1 ⇒ r = 5 − 2 ⇒ r = 3

14. Questão 2: Determine a razão, sabendo que A8 = 14 e A1 = 0.
An= A1 + ( n – 1 ). r
An = 0 + (8 – 1). r
An = A8 = 14
14 = 0 + 7 . r
A1 = 0
14 = 7r
n =8
r = 14 / 7
r =?
r=2

15. AGORA TENTE FAZER SOZINHO.
Determine o sexto termo de uma P.A. onde A1 =-3er=5
 Só para relembrar A1 é o primeiro termo e r é a
razão.

16. SUBSTITUA NA FÓRMULA OS TERMOS QUE
VOCÊ POSSUI
A1 = - 3
r= 5
 n = 6, pois é o sexto termo dessa P.A.
An = ?
An = A1 + ( n – 1 ). r
An = - 3+ ( 6 – 1 ). 5
An = - 3+ 5 . 5
An = - 3 + 25
An = 22

17. INTERPOLAÇÃO
Agora um outro exercício de P.A. que se chama interpolação.
Este tipo de problema consiste em descobrir a razão, para
podermos determinar os elementos dessa P.A., onde são dados
dois valores (que são as extremidades) e a quantidades de
termos que ficam entre essas extremidades, chamamos de
interpolar.
Exemplo:
Faça a interpolação de cinco meios aritméticos entre - 8 e 22.
Neste caso devemos descobrir cinco números entre - 8 e 22
que formem juntamente com estes a seguinte P.A.

18. 6 RAZÕES
( − 8, A2 , A3 , A4 , A5 , A6 ,22)
↑ ↑
A1 5 meios A7
O problema fica resolvido com a determinação da razão da P.A.
Como A1 = - 8 e A7 = 22, então:
A7 = A1 + 6 . r ⇒ 22 = - 8 + 6 . r ⇒ r = 5
Os números procurados são - 3, 2, 7, 12, 17 e a P.A. é (- 8, - 3,
2, 7, 12, 17, 22)

19. Obs: Entre – 8 e 22 existem 6 razões, por isso na montagem
da expressão multiplicamos 6. r.
O número que se multiplica pela razão irá varias de acordo com a
quantidades de termos.
1 2 3 4 5 6
( − 8, A2 , A3 , A4 , A5 , A6 ,22)

20. AGORA TENTE FAZER ESTE EXERCÍCIO.
1 - (FATES) - Interpolar 10 meios aritméticos entre 2 e 57 e
escrever a P. A. correspondente com primeiro termo igual a 2.
Lembre-se que é
preciso determinar a
razão!

21. 11 RAZÕES
( 2, A2 , A3 , A4 , A5 , A6 , A7 , A8 , A9 , A10 , A11 ,57 )
↑ ↑
A1 A12
10 meios
(são 10 termos entre as extremidades que são 2 e 57)
A12= A1 + 11 . r
10 = 2 + 11 . r
57- 2 = 11r
r = 55/11
r=5

22. SOMA DOS TERMOS DE UMA P.A. FINITA
Podemos definir a soma dos termos de uma P.A. finita através
da fórmula:
( A1 + An ).n
Sn =
2
Onde:
Sn ⇒ soma dos termos de uma P.A. finita
A1 ⇒ primeiro termo
An ⇒ termo geral
n ⇒ número de termos

23. EXEMPLO
Calcule a soma dos doze primeiros termos da P.A. (- 3, -1, 1, 3,
...).
 Neste caso devemos primeiro determinar o valor de An através
da fórmula do termo geral.
An = A1 + (n − 1).r An = A1 + (n − 1).r
A2 A1 An = −3 + (12 − 1).2
r= -
r = (-1) – (-3) An = −3 + 22
r=2 An = 19

24. Agora podemos utilizar a fórmula de somatória dos termos da
P.A. , já que temos os elementos necessários:
( A1 + An ).n An = 19
Sn =
2
( −3 +19).12 A1 = −3
Sn =
2
Sn =
16.12 n = 12
2
192
Sn = ⇒96
2

25. AGORA TENTE FAZER SOZINHO!
2 - (PUC-SP) - Determine uma P.A. sabendo que a
soma de seus 8 primeiros termos é 324 e que A8 = 79.

26. Solução:
( A1 + An ).n
Sn =
2 An = A1 + (n − 1).r
( A1 + 79).8
324 = 79 = 2 + (8 − 1).r
2
79 = 2 + 7 r
324.2 = (8 A1 + 632)
648 = (8 A1 + 632)
7 r = 77
648 −632 = 8 A1 r = 77 / 7
16 r = 11
A1 = ⇒2
8

27. SENDO ASSIM OS ELEMENTOS DESSA P.A, SÃO
(2, 13, 24, 35, 46, 57, 68, 79)
Poderemos calcular qualquer termo
das fórmulas gerais desde de que
sejam conhecidos três desses quatro
valores!

28. BIBLIOGRAFIA
FACCHINI,Walter. Matemática Volume Único. Editora
Saraiva, 2007.
BACCARO, Nelson. Matemática; 2ºgrau. Editora
Ática,1995.